Файл: Контрольная работа по дисциплине эконметрика Студент (Ф. И. О.) Толибова Фотиманисо Мухторкизи Группа кэ12.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 50
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
увеличение запасов ресурсов, требующее распределения дополнительных вложений.
Из вышеизложенного следует, что статус ресурсов (дефицитный или недефицитный) для любой модели линейного программирования можно установить непосредственно из результирующей симплекс-таблицы, обращая внимание на значения выравнивающих переменных. Применительно к нашей задаче можно привести следующую сводную таблицу:
Положительное значение выравнивающей переменной указывает на неполное использование соответствующего ресурса, т. е. данный ресурс является недефицитным. Если же выравнивающая переменная равна 0, то это свидетельствует о полном потреблении соответствующего ресурса. Из сводной таблицы видно, что ресурсы 2 и 4 связаны с запасами сырья В и возможностями сбыта продукции П2. Поэтому любое увеличение их запасов сверх установленного' максимального значения приведет лишь к тому, что они станут еще более недефицитными. Оптимальное решение задачи при этом останется неизменным.
Ресурсы, увеличение запасов которых позволяет улучшить решение (увеличить доход), - это сырье А и возможности по сбыту продукции П1, поскольку из оптимальной симплекс-таблицы вид' но, что они дефицитные. В связи с этим логично поставить вопрос: какому из дефицитных ресурсов следует отдать предпочтение при вложении дополнительных средств на увеличение их запасов, с тем чтобы получить от них максимальную отдачу? Ответ на этот вопрос будет дан в следующем разделе этой главы, где рассматривается ценность различных ресурсов.
Ценность ресурса
Ценность ресурса характеризуется величиной улучшения оптимального значения Z, приходящегося на единицу прироста объема данного ресурса. Графическая интерпретация этого определения применительно к условиям задачи об ассортименте продукции была дана в п. 8.4 (вторая задача на чувствительность). Графический анализ показывает, что ценность ресурсов 1, 2, 3 и 4 равна:
U1 = 1,4 д. е. на единицу прироста запасов ресурса сырья А;
U2= О, U4 = 0;
U3= 0,2 д. е. на единицу прироста превышения производства продукции П1 по отношению к объему производства продукции П2
Эта информация представлена в оптимальной таблице. Обратим внимание на значения коэффициентов Z-уравнения, стоящих при переменных начального базиса у1,у2, у3и у4. Значения указанных коэффициентов (1,4; 0; 0,2; 0) в точности соответствуют значениям U1, U2 U3 U4.
Хотя в п. 8.4 были даны необходимые разъяснения, связанные с определением ценности ресурсов, покажем, каким образом аналогичный результат можно получить непосредственно из симплекс-таблицы.
Рассмотрим Z-уравнение оптимальной симплекс-таблицы решения задачи об ассортименте продукции:
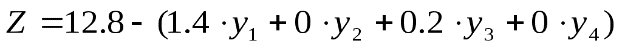
Положительное приращение переменной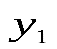 относительно ее текущего нулевого значения приводит к пропорциональному уменьшению Z, причем коэффициент пропорциональности равен 1,4 д. е. Однако из первого ограничения модели следует
относительно ее текущего нулевого значения приводит к пропорциональному уменьшению Z, причем коэффициент пропорциональности равен 1,4 д. е. Однако из первого ограничения модели следует
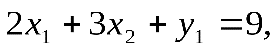
т. е. увеличение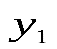 эквивалентно снижению запаса ресурса 1 (сырья А). Отсюда следует, что уменьшение запаса первого ресурса вызывает пропорциональное уменьшение целевой функции Z c коэффициентом пропорциональности, равным 1,4 д. е. Аналогичные рассуждения справедливы и для ресурса 3.
эквивалентно снижению запаса ресурса 1 (сырья А). Отсюда следует, что уменьшение запаса первого ресурса вызывает пропорциональное уменьшение целевой функции Z c коэффициентом пропорциональности, равным 1,4 д. е. Аналогичные рассуждения справедливы и для ресурса 3.
В отношении ресурсов 2 и 4 было установлено, что их ценность равна 0
(U2 = U4=0). Этого и следовало ожидать, так как ресурсы .2и4 оказались недефицитными. Такой результат получается всякий раз, когда соответствующие выравнивающие переменные имеют положительное значение.
Несмотря на то что ценность различных ресурсов, определяемая значениями переменных Uiбыла представлена в стоимостном (д. е.) выражении, ее нельзя отождествлять с действительными ценами, по которым возможна закупка соответствующих ресурсов. На самом деле речь идет о некоторой мере, имеющей экономическую природу и количественно характеризующей ценность ресурса только относительно полученного оптимального значения Z. При изменении ограничений модели соответствующие экономические оценки будут меняться даже тогда, когда оптимизируемый процесс предполагает применение тех же ресурсов. Поэтому при характеристике ценности ресурсов экономисты предпочитают использовать такие термины, как теневая цена или двойственная оценка. Заметим, что теневая цена характеризует интенсивность улучшения оптимального решения Z. Однако при этом не фиксируется интервал значений увеличения запасов ресурсов, при которых интенсивность улучшения целевой функции остается постоянной. Для большинства практических ситуаций логично предположить наличие верхнего предела увеличения запасов, при превышении которого соответствующее ограничение становится избыточным, что в свою очередь приводит к новому базисному решению и соответствующим ему новым теневым ценам. Ниже определяется интервал значений запасов ресурса, при которых соответствующее ограничение не становится избыточным.
Максимальное изменение запаса ресурса
При решении вопроса о том, запас какого из ресурсов следует увеличивать в первую очередь, обычно используются двойственные оценки (теневые цены). Чтобы определить интервал значений изменения запаса ресурса, при которых двойственная оценка данного ресурса, фигурирующая в заключительной симплекс-таблице, остается неизменной, необходимо выполнить ряд дополнительных вычислений. Положим, что в задаче об ассортименте продукции запас первого ресурса (сырья А) изменился на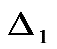 т. е. запас сырья А составит (9 +
т. е. запас сырья А составит (9 + 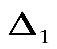 ) единиц. Введем это изменение в начальную симплекс-таблицу и затем выполним всю последовательность вычислений.
) единиц. Введем это изменение в начальную симплекс-таблицу и затем выполним всю последовательность вычислений.
Поскольку элементы правых частей ограничений никогда не используются в качестве разрешающих, то очевидно, что на каждой итерации вычислений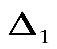 будет оказывать влияние только на значения элементов столбца «свободные члены».
будет оказывать влияние только на значения элементов столбца «свободные члены».
Результаты вычислений элементов столбца «свободные члены» сведены в следующую таблицу:
Все изменения элементов столбца «свободные члены» опре; ляются непосредственно по данным, содержащимся в симплекс-таблицах. Каждый элемент столбца «свободные члены» представляет собой сумму двух величин: 1) постоянной и 2) члена, линейно зависящего от ,. Постоянные соответствуют числам, которые фигурируют в оптимальной симплекс-таблице до введения
,. Постоянные соответствуют числам, которые фигурируют в оптимальной симплекс-таблице до введения  , в столбце «свободные члены». Коэффициенты при
, в столбце «свободные члены». Коэффициенты при  , во вторых слагаемых равны коэффициентам при у1в оптимальной симплекс-таблице.
, во вторых слагаемых равны коэффициентам при у1в оптимальной симплекс-таблице.
Заметим, что при анализе изменений в правых частях второго, третьего и четвертого ограничений нужно пользоваться коэффициентами при переменных у2, y3, y4соответственно.
Так как введение сказывается лишь на правой части ограничений (на элементах столбца «свободные члены»), изменение запаса ресурса может повлиять только на допустимость решения. Поэтому
сказывается лишь на правой части ограничений (на элементах столбца «свободные члены»), изменение запаса ресурса может повлиять только на допустимость решения. Поэтому  не может принимать значений, при которых какая-либо из базисных переменных становится отрицательной. Из этого следует, что величина
не может принимать значений, при которых какая-либо из базисных переменных становится отрицательной. Из этого следует, что величина  должна быть ограничена таким интервалом значений, при котором выполняется условие неотрицательности правых частей ограничений в результирующей симплекс-таблице, т. е.:
должна быть ограничена таким интервалом значений, при котором выполняется условие неотрицательности правых частей ограничений в результирующей симплекс-таблице, т. е.:
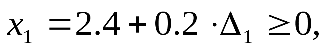 (8.51)
(8.51)
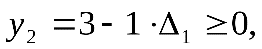 (8.52)
(8.52)
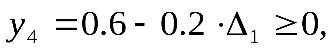
Из вышеизложенного следует, что статус ресурсов (дефицитный или недефицитный) для любой модели линейного программирования можно установить непосредственно из результирующей симплекс-таблицы, обращая внимание на значения выравнивающих переменных. Применительно к нашей задаче можно привести следующую сводную таблицу:
| Ресурс | Выравнивающая переменная | Статус ресурса |
| Сырье А | y1=0 | Дефицитный |
| Сырье В | y2=3 | Недефицитный |
| Превышение объема производства продукции /7, по отношению к объему производства продукции П2 | y3=0 | Дефицитный |
| Спрос на продукцию П2 | y4=0.6 | Недефицитный |
Положительное значение выравнивающей переменной указывает на неполное использование соответствующего ресурса, т. е. данный ресурс является недефицитным. Если же выравнивающая переменная равна 0, то это свидетельствует о полном потреблении соответствующего ресурса. Из сводной таблицы видно, что ресурсы 2 и 4 связаны с запасами сырья В и возможностями сбыта продукции П2. Поэтому любое увеличение их запасов сверх установленного' максимального значения приведет лишь к тому, что они станут еще более недефицитными. Оптимальное решение задачи при этом останется неизменным.
Ресурсы, увеличение запасов которых позволяет улучшить решение (увеличить доход), - это сырье А и возможности по сбыту продукции П1, поскольку из оптимальной симплекс-таблицы вид' но, что они дефицитные. В связи с этим логично поставить вопрос: какому из дефицитных ресурсов следует отдать предпочтение при вложении дополнительных средств на увеличение их запасов, с тем чтобы получить от них максимальную отдачу? Ответ на этот вопрос будет дан в следующем разделе этой главы, где рассматривается ценность различных ресурсов.
Ценность ресурса
Ценность ресурса характеризуется величиной улучшения оптимального значения Z, приходящегося на единицу прироста объема данного ресурса. Графическая интерпретация этого определения применительно к условиям задачи об ассортименте продукции была дана в п. 8.4 (вторая задача на чувствительность). Графический анализ показывает, что ценность ресурсов 1, 2, 3 и 4 равна:
U1 = 1,4 д. е. на единицу прироста запасов ресурса сырья А;
U2= О, U4 = 0;
U3= 0,2 д. е. на единицу прироста превышения производства продукции П1 по отношению к объему производства продукции П2
Эта информация представлена в оптимальной таблице. Обратим внимание на значения коэффициентов Z-уравнения, стоящих при переменных начального базиса у1,у2, у3и у4. Значения указанных коэффициентов (1,4; 0; 0,2; 0) в точности соответствуют значениям U1, U2 U3 U4.
Хотя в п. 8.4 были даны необходимые разъяснения, связанные с определением ценности ресурсов, покажем, каким образом аналогичный результат можно получить непосредственно из симплекс-таблицы.
Рассмотрим Z-уравнение оптимальной симплекс-таблицы решения задачи об ассортименте продукции:
Положительное приращение переменной
т. е. увеличение
В отношении ресурсов 2 и 4 было установлено, что их ценность равна 0
(U2 = U4=0). Этого и следовало ожидать, так как ресурсы .2и4 оказались недефицитными. Такой результат получается всякий раз, когда соответствующие выравнивающие переменные имеют положительное значение.
Несмотря на то что ценность различных ресурсов, определяемая значениями переменных Uiбыла представлена в стоимостном (д. е.) выражении, ее нельзя отождествлять с действительными ценами, по которым возможна закупка соответствующих ресурсов. На самом деле речь идет о некоторой мере, имеющей экономическую природу и количественно характеризующей ценность ресурса только относительно полученного оптимального значения Z. При изменении ограничений модели соответствующие экономические оценки будут меняться даже тогда, когда оптимизируемый процесс предполагает применение тех же ресурсов. Поэтому при характеристике ценности ресурсов экономисты предпочитают использовать такие термины, как теневая цена или двойственная оценка. Заметим, что теневая цена характеризует интенсивность улучшения оптимального решения Z. Однако при этом не фиксируется интервал значений увеличения запасов ресурсов, при которых интенсивность улучшения целевой функции остается постоянной. Для большинства практических ситуаций логично предположить наличие верхнего предела увеличения запасов, при превышении которого соответствующее ограничение становится избыточным, что в свою очередь приводит к новому базисному решению и соответствующим ему новым теневым ценам. Ниже определяется интервал значений запасов ресурса, при которых соответствующее ограничение не становится избыточным.
Максимальное изменение запаса ресурса
При решении вопроса о том, запас какого из ресурсов следует увеличивать в первую очередь, обычно используются двойственные оценки (теневые цены). Чтобы определить интервал значений изменения запаса ресурса, при которых двойственная оценка данного ресурса, фигурирующая в заключительной симплекс-таблице, остается неизменной, необходимо выполнить ряд дополнительных вычислений. Положим, что в задаче об ассортименте продукции запас первого ресурса (сырья А) изменился на
Поскольку элементы правых частей ограничений никогда не используются в качестве разрешающих, то очевидно, что на каждой итерации вычислений
Результаты вычислений элементов столбца «свободные члены» сведены в следующую таблицу:
| Уравнение | Значения элементов столбца «свободные члены» | |
| Начальная симплекс-таблица | Оптимальная симплекс-таблица | |
| Z | 0 | |
| 1 | 9+ | |
| 2 | 13 | |
| 3 | 1 | |
| 4 | 2 | |
Все изменения элементов столбца «свободные члены» опре; ляются непосредственно по данным, содержащимся в симплекс-таблицах. Каждый элемент столбца «свободные члены» представляет собой сумму двух величин: 1) постоянной и 2) члена, линейно зависящего от
Заметим, что при анализе изменений в правых частях второго, третьего и четвертого ограничений нужно пользоваться коэффициентами при переменных у2, y3, y4соответственно.
Так как введение