Файл: Контрольная работа по дисциплине эконметрика Студент (Ф. И. О.) Толибова Фотиманисо Мухторкизи Группа кэ12.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 51
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(8.53)
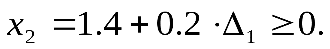 (8.54)
(8.54)
Для определения допустимого интервала изменения рассмотрим два случая.
рассмотрим два случая.
Случай 1: > 0.
> 0.
Соотношения (8.51) и (8.54) всегда выполняются при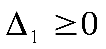 . Соотношения (8.52) и (8.53) определяют следующие предельные значения
. Соотношения (8.52) и (8.53) определяют следующие предельные значения 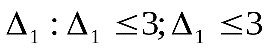 . Таким образом, все четыре соотношения выполняются при
. Таким образом, все четыре соотношения выполняются при 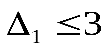 .
.
Случай 2: < 0.
< 0.
Соотношения (8.52) и (8.53) выполняются при < 0. Соотношения (7.51) и (7.54) справедливы при
< 0. Соотношения (7.51) и (7.54) справедливы при 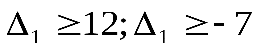 соответственно.
соответственно.
Таким образом, оба соотношения справедливы при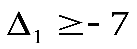 .
.
Объединяя результаты, полученные для обоих случаев, можно сделать вывод, что при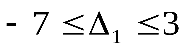 решение рассматриваемой системы всегда будет допустимым. Любое значение
решение рассматриваемой системы всегда будет допустимым. Любое значение  , выходящее за предел указанного интервала (т.е. уменьшение запаса сырья А более чем на 7 единиц или увеличение более чем на 3 единицы), приведет к недопустимости решения и новой совокупности базисных переменных.
, выходящее за предел указанного интервала (т.е. уменьшение запаса сырья А более чем на 7 единиц или увеличение более чем на 3 единицы), приведет к недопустимости решения и новой совокупности базисных переменных.
Анализ на чувствительность оптимального решения к вариации коэффициентов целевой функции
В п. 8.4 на основе графического представления модели было показано
, что при определенных значениях изменения коэффициентов целевой функции оптимальные значения переменных остаются неизменными (хотя оптимальное значение Z при этом меняется). Возвращаясь к этому вопросу, покажем, каким образом интересующую нас информацию можно получить из данных, содержащихся в оптимальной симплекс-таблице.
Следует отметить, что уравнение целевой функции также не используется в качестве ведущего уравнения. Поэтому любые изменения коэффициентов целевой функции окажут влияние только на Z-уравнение результирующей симплекс-таблицы. Это означает, что такие изменения могут сделать полученное решение неоптимальным. Наша цель заключается в том, чтобы найти интервалы изменений коэффициентов целевой функции, при которых оптимальные значения переменных остаются неизменными.
Чтобы показать, как выполняются соответствующие вычисления, положим, что доход, получаемый с единицы продукции П1, изменяется от 3 до 3 +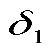 где
где 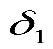 может быть как положительным, так и отрицательным числом. Целевая функция в этом случае принимает следующий вид:
может быть как положительным, так и отрицательным числом. Целевая функция в этом случае принимает следующий вид:
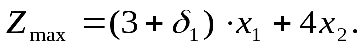
Если воспользоваться данными начальной симплекс-таблицы и выполнить все вычисления, необходимые для получения оптимальной симплекс-таблицы, то последнее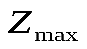 -уравнение будет выглядеть следующим образом:
-уравнение будет выглядеть следующим образом:
Это уравнение (строка целевой функции) отличается от Z-уравнения до введения только наличием членов, содержащих
только наличием членов, содержащих  . Коэффициенты при
. Коэффициенты при  равны коэффициентам при соответствующих переменных в x1 - уравнении (x1-строка) симплекс-таблицы для полученного ранее оптимального решения:
равны коэффициентам при соответствующих переменных в x1 - уравнении (x1-строка) симплекс-таблицы для полученного ранее оптимального решения:
Мы рассматриваем x1-уравнение, так как коэффициент именно при этой переменной в выражении для целевой функции в начальной симплекс-таблице изменился на .
.
Оптимальные значения переменных будут оставаться неизменными при значениях удовлетворяющих условию неотрицательности (задача на отыскание максимума) всех коэффициентов при свободных переменных в Z-уравнении. Таким образом, должны выполняться следующие неравенства:
удовлетворяющих условию неотрицательности (задача на отыскание максимума) всех коэффициентов при свободных переменных в Z-уравнении. Таким образом, должны выполняться следующие неравенства:
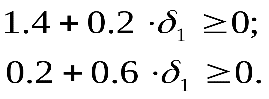
Из первого неравенства получаем, что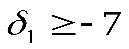 , а из второго следует, что
, а из второго следует, что 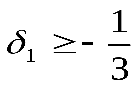 . Эти результаты определяют пределы изменения коэффициента
. Эти результаты определяют пределы изменения коэффициента 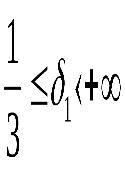 .
.
Таким образом, при уменьшении коэффициента целевой функции при переменной x1до значения, равного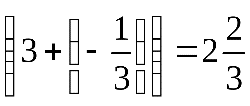 , или при его увеличении до
, или при его увеличении до 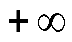
оптимальные значения переменных остаются неизменными. Этот вывод совпадает с результатом, полученным в п. 7.4.
Следует отметить, что оптимальное значение Z будет изменяться в соответствии с выражением (12,8 + 2,4 ), где
), где 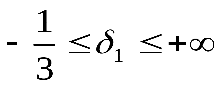 .
.
Мы рассмотрели случай изменения коэффициента при базисной переменной x1. В случае изменения коэффициента при свободной переменной в целевой функции происходит изменение коэффициента только при данной переменной в оптимальной симплекс-таблице. Рассмотрим в качестве иллюстрации случай, когда коэффициент при свободной переменной y1 (первая выравнивающая переменная) изменяется от 0 до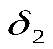 . Выполнение преобразований, необходимых для получения заключительной симплекс-таблицы, приводит к следующему результирующему Z-уравнению:
. Выполнение преобразований, необходимых для получения заключительной симплекс-таблицы, приводит к следующему результирующему Z-уравнению:
Из приведенного фрагмента заключительной симплекс-таблицы видно, что единственное отличие от Z-уравнения до введения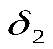 состоит в том, что коэффициент при у3 уменьшился на
состоит в том, что коэффициент при у3 уменьшился на 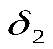 . Таким образом, коэффициент при свободной переменной в результирующем Z-уравнении нужно уменьшить на ту же величину, на которую он увеличивался в исходном Z-уравнении
. Таким образом, коэффициент при свободной переменной в результирующем Z-уравнении нужно уменьшить на ту же величину, на которую он увеличивался в исходном Z-уравнении
Для определения допустимого интервала изменения
Случай 1:
Соотношения (8.51) и (8.54) всегда выполняются при
Случай 2:
Соотношения (8.52) и (8.53) выполняются при
Таким образом, оба соотношения справедливы при
Объединяя результаты, полученные для обоих случаев, можно сделать вывод, что при
Анализ на чувствительность оптимального решения к вариации коэффициентов целевой функции
В п. 8.4 на основе графического представления модели было показано
, что при определенных значениях изменения коэффициентов целевой функции оптимальные значения переменных остаются неизменными (хотя оптимальное значение Z при этом меняется). Возвращаясь к этому вопросу, покажем, каким образом интересующую нас информацию можно получить из данных, содержащихся в оптимальной симплекс-таблице.
Следует отметить, что уравнение целевой функции также не используется в качестве ведущего уравнения. Поэтому любые изменения коэффициентов целевой функции окажут влияние только на Z-уравнение результирующей симплекс-таблицы. Это означает, что такие изменения могут сделать полученное решение неоптимальным. Наша цель заключается в том, чтобы найти интервалы изменений коэффициентов целевой функции, при которых оптимальные значения переменных остаются неизменными.
Чтобы показать, как выполняются соответствующие вычисления, положим, что доход, получаемый с единицы продукции П1, изменяется от 3 до 3 +
Если воспользоваться данными начальной симплекс-таблицы и выполнить все вычисления, необходимые для получения оптимальной симплекс-таблицы, то последнее
| Свободные переменные | Свободные члены | y1 | y2 |
| | | 1.4+0.2 | 0.2+0.6 |
Это уравнение (строка целевой функции) отличается от Z-уравнения до введения
| Свободные неиз-вестные Базисные неизвестные | Свободный Член | y1 | y3 |
| x1 | 2.4 | 0.2 | 0.6 |
Мы рассматриваем x1-уравнение, так как коэффициент именно при этой переменной в выражении для целевой функции в начальной симплекс-таблице изменился на
Оптимальные значения переменных будут оставаться неизменными при значениях
Из первого неравенства получаем, что
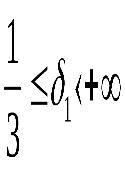 .
.Таким образом, при уменьшении коэффициента целевой функции при переменной x1до значения, равного
оптимальные значения переменных остаются неизменными. Этот вывод совпадает с результатом, полученным в п. 7.4.
Следует отметить, что оптимальное значение Z будет изменяться в соответствии с выражением (12,8 + 2,4
Мы рассмотрели случай изменения коэффициента при базисной переменной x1. В случае изменения коэффициента при свободной переменной в целевой функции происходит изменение коэффициента только при данной переменной в оптимальной симплекс-таблице. Рассмотрим в качестве иллюстрации случай, когда коэффициент при свободной переменной y1 (первая выравнивающая переменная) изменяется от 0 до
| Свободные неизвестные | Свободный член | y1 | y2 |
| Zmax | 12.8 | 1.4- | 0.2 |
Из приведенного фрагмента заключительной симплекс-таблицы видно, что единственное отличие от Z-уравнения до введения