ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 23
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

• PUBLIC 公開
Исходные данные для варианта №42
| № варианта | a | b | c | d | p |
| 42 | 3700 | 150 | 1,3 | 0,01 | 200 |
Задана функция общих издержек совершенно конкурентной фирмы
TC=3700+150*Q-1,3*Q^2+0,01*Q^3
Ход выполнения работы
1. Пусть Q=10; 20; 30;..;200.
Необходимо в первую очередь определить алгебраические выражения издержек в краткосрочном периоде.
FC-это затраты, которые не зависят от объема выпуска продукции, следовательно по данной формуле TC = а + b*Q – c*Q^2+ d*Q^3, необходимо выделить факторы, которые не зависят от объема выпуска.
По исходным данным получаем формулу TC=3700+150*Q-1,3*Q^2+0,01*Q^3, из которой можно выделить, что независящий от объема производства фактор равняется 3700.
FC=3700
VC-затраты, величина которых зависит от объема выпуска продукции.
VC=(3700+150*Q-1,3*Q^2+0,01*Q^3)-3700
Раскрываем скобки и сокращаем, получается
VC=150*Q-1,3*Q^2+0,01*Q^3
AFC-это постоянные затраты, которые приходятся на единицу продукции
AFC=3700/Q
AVC-переменные затраты, приходящиеся по единицу продукции
AVC=(150*Q-1,3*Q^2+0,01*Q^3)/Q
ATC-это средние общие затраты, показывающие общие затраты на единицу продукции
ATC=(3700+150*Q-1,3*Q^2+0,01*Q^3)/Q
ATC=3700/Q+150-1,3*Q+0,01*Q^2
MC-предельные затраты, отражающие дополнительные затраты на дополнительную единицу продукции
MC=(3700+150*Q-1,3*Q^2+0,01*Q^3)’
MC=150-2,6*Q+0,03*Q^2
Для подсчета все выведенные формулы были выведены в таблицы EXCEL, где были получены следующие результаты.
| Таблица №1 | |||
| Q | TC | FC | VC |
| 10 | 3037 | 2500 | 537 |
| 20 | 3476 | 2500 | 976 |
| 30 | 3859 | 2500 | 1359 |
| 40 | 4228 | 2500 | 1728 |
| 50 | 4625 | 2500 | 2125 |
| 60 | 5092 | 2500 | 2592 |
| 70 | 5671 | 2500 | 3171 |
| 80 | 6404 | 2500 | 3904 |
| 90 | 7333 | 2500 | 4833 |
| 100 | 8500 | 2500 | 6000 |
| 110 | 9947 | 2500 | 7447 |
| 120 | 11716 | 2500 | 9216 |
| 130 | 13849 | 2500 | 11349 |
| 140 | 16388 | 2500 | 13888 |
| 150 | 19375 | 2500 | 16875 |
| 160 | 22852 | 2500 | 20352 |
| 170 | 26861 | 2500 | 24361 |
| 180 | 31444 | 2500 | 28944 |
| 190 | 36643 | 2500 | 34143 |
| 200 | 42500 | 2500 | 40000 |
| Таблица №2 | ||||
| Q | AFC | AVC | ATC | MC |
| 10 | 250,00 | 53,70 | 303,70 | 48,10 |
| 20 | 125,00 | 48,80 | 173,80 | 40,40 |
| 30 | 83,33 | 45,30 | 128,63 | 36,90 |
| 40 | 62,50 | 43,20 | 105,70 | 37,60 |
| 50 | 50,00 | 42,50 | 92,50 | 42,50 |
| 60 | 41,67 | 43,20 | 84,87 | 51,60 |
| 70 | 35,71 | 45,30 | 81,01 | 64,90 |
| 80 | 31,25 | 48,80 | 80,05 | 82,40 |
| 90 | 27,78 | 53,70 | 81,48 | 104,10 |
| 100 | 25,00 | 60,00 | 85,00 | 130,00 |
| 110 | 22,73 | 67,70 | 90,43 | 160,10 |
| 120 | 20,83 | 76,80 | 97,63 | 194,40 |
| 130 | 19,23 | 87,30 | 106,53 | 232,90 |
| 140 | 17,86 | 99,20 | 117,06 | 275,60 |
| 150 | 16,67 | 112,50 | 129,17 | 322,50 |
| 160 | 15,63 | 127,20 | 142,83 | 373,60 |
| 170 | 14,71 | 143,30 | 158,01 | 428,90 |
| 180 | 13,89 | 160,80 | 174,69 | 488,40 |
| 190 | 13,16 | 179,70 | 192,86 | 552,10 |
| 200 | 12,50 | 200,00 | 212,50 | 620,00 |
По данным результатам, отраженных в таблице №1 и таблице №2, были составлены графики к таблице №1 и таблице №2 соответственно.
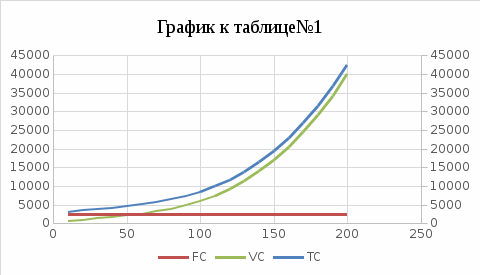
Вывод к графику к таблице №1
Кривая переменных издержек возрастает медленно, также наблюдается средний рост при объеме выпуска равному 60. Вследствие чего можно сделать, что на первоначальных этапах производства предприятие придерживается тенденции экономии. С увеличением объема выпуска замечается более активный рост переменных издержек-издержки резко увеличиваются.
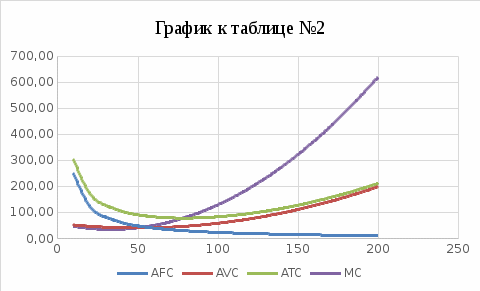
Вывод к графику к таблице №2
На графике видно, что с увеличением объема выпуска средние постоянные издержки сокращаются, что для предприятия в свою очередь служит мощным стимулом для увеличения производства. Средние переменные издержки можно охарактеризовать плавным ростом, в следствии чего можно отметить, что производство будет эффективным и относительно не дорогостоящим. График средних общих издержек сначала убывает, а затем возрастает и сближается с кривой AVC. Предельные издержки постепенно возрастают. MC больше AVC и ATC (их кривые идут вверх) что означает, что производство каждой новой единицы продукции увеличивает средние переменные и средние совокупные издержки.
2. На графике к таблице №2 видно, что в точке пересечения средних и предельных издержек оптимальный объем равен 90.
Найдем оптимальный выпуск аналитически. Для этого необходимо составить уравнение, приравняв функции ATC и MC.
2500/Q+60-0.7*Q+0.007*Q^2=60-1.4*Q+0.021*Q^2;
0.014*Q^2-0.7*Q-2500/Q=0
3700/Q+150-1,3*Q+0,01*Q^2=150-2,6*Q+0,03*Q^2
0,02*Q^2-1,3*Q-3700/Q=0
Для более точных подсчетов была создана таблица №3, где отражены значения Q и результаты подсчетов получившегося уравнения. По таблице видно, что наиболее точное значение Qопт. = 88,6, округляем в большую сторону до целого числа Qопт.=89.
Точность решения по сравнению с графическим методом (90/89-1)*100=1,1%
3. Используя условие максимизации прибыли MC=MR=p, определим какой объем выпуска выберет фирма для получения максимальной прибыли. Приравниваем функцию издержек к цене товара равной 200.
60-1,4*Q+0.021*Q^2=200
150-2,6*Q+0,03*Q^2=200
Получаем корни уравнения
Q1=-54.86;
Q2=121.53.
Q1=-16,21;
Q2=102,86.
Так как первый корень уравнения отрицательный, то получаем, что фирма выберет объем выпуска равный 102,86 121.53 (по данным таблицы №1 приравниваем к максимально приближенному значению 100 120).
TR=p*Q
TR=200*102,86=20572 ден.ед.
TC=3700+150*Q-1,3*Q^2+0,01*Q^3
TC=3700+150*102,86-1,3*102,86^2+0,01*102,86^3=16257,53 ден.ед.
Pr=TR-TC, TC при объеме производства 102,86 равно 16257,53 11716
Pr=24000-11716=12284
Pr=20572-16257,53=4314,47 ден.ед.
Прибыль при объеме выпуска 120 равен 12284.
Прибыль при объеме выпуска 102,86 равен 4314,47 ден.ед.
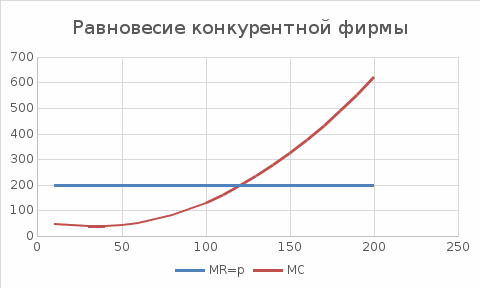
Вывод: в ходе работы мной был проведен анализ издержек в краткосрочном периоде, определен оптимальный объем производства и выпуска, так же была выведена максимальная прибыль предприятия, сформированы и описаны графики.