Файл: Решение. Для решения задания воспользуемся методом математической индукции. Пусть.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 12
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Доказать, что при любом натуральном n,
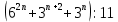.Решение.
Для решения задания воспользуемся методом математической индукции. Пусть
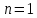(наименьшее натуральное число). Тогда: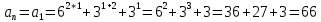
Поскольку Число 66 делится на 11, то при
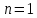исходное утверждение является верным (число 
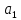делится на 11).Предположим, что для произвольного натурального числа
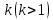исходное утверждение верно, то есть, число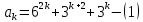
Делится на 11. Покажем, что в этом случае утверждение верно и для числа k+1. Выражение:
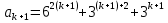
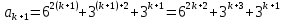
Преобразуем его:
Индивидуальное задание № 1 по теме «Матрицы и определители»
1. Сложить матрицы:
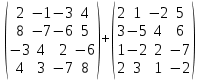
Решение.
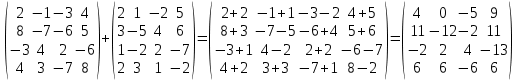
2. Умножить матрицы:
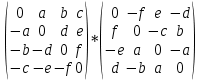
Решение.
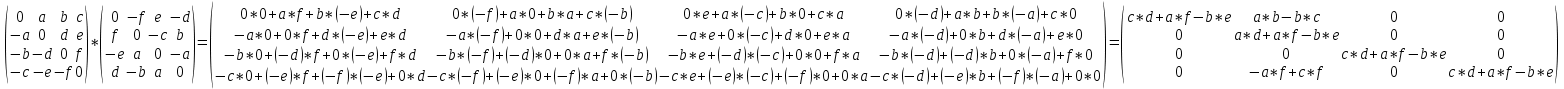
3. Выполнить действия:
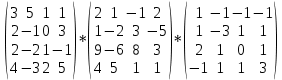
Решение.
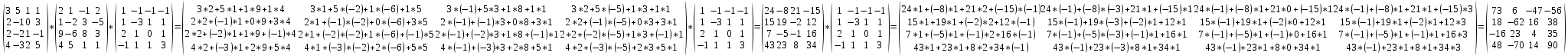
4. Решить систему методом Крамера:
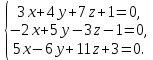
Решение.
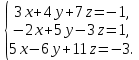
Подсчитаем сначала главный определитель системы
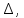воспользовавшись следующим правилом вычисления определителей третьего порядка: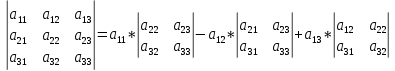
В нашем случае главный определитель равен:
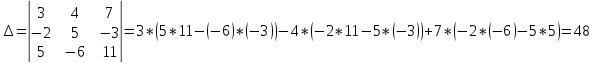
Так как
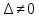, делаем вывод о том, что система имеет единственное решение. Для его отыскания вычислим вспомогательные определители 
:
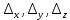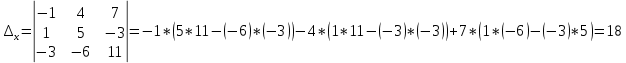
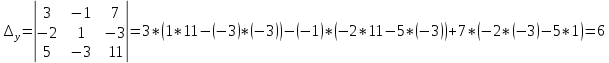
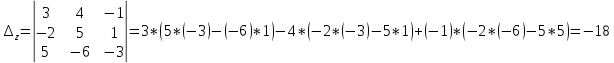
Далее, воспользовавшись формулами Крамера, окончательно получим:
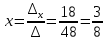
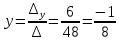
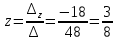
5. Найти обратную матрицу (двумя способами) для:
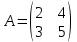
Решение.
а) Найдем матрицу
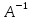с помощью элементарных преобразованийОпределитель матрицы А
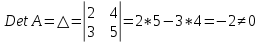
Следовательно, матрица А не выражена и поэтому имеет обратную матрицу.
Найдем обратную матрицу с помощью элементарных преобразований, для этого припишем справа единичную матрицу такого же размера. Первую строку делим на 2. От второй строки отнимаем первую строку, умноженную на 3. Вторую строку умножаем на (-1). От первой строки отнимаем 2 строку, умноженную на 2.
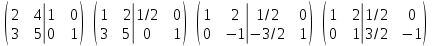
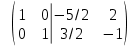
Следовательно обратная матрица:
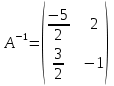
б) Найдем матрицу
с помощью явной формулы (через присоединенную матрицу).Определитель матрицы А
Следовательно, матрица А не выражена и поэтому имеет обратную матрицу.
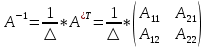
Где
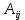– алгебраическое дополнение, соответствующее элементу 
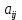. В данном случае
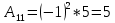
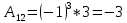
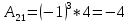
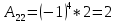
Отсюда обратная матрица:
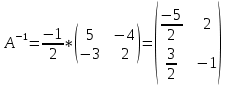
6. Вычислить определители:
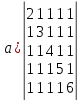
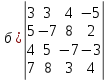
Решение.
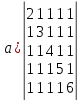
Приведем матрицу к ступенчатому виду. Операция добавления к одной из строк матрицы другой строки, умноженной на некоторое число, не меняет определитель. Определитель преобразованной матрицы равен определителю исходной.
Вычитаем из строки 2 строку 1, умноженную на (1/2). Вычитаем из строки 3 строку 1, умноженную на (1/2). Вычитаем из строки 4 строку 1, умноженную на (1/2). Вычитаем из строки 5 строку 1, умноженную на (1/2). Вычитаем из строки 3 строку 2, умноженную на (1/5). Вычитаем из строки 4 строку 2, умноженную на (1/5). Вычитаем из строки 5 строку 2, умноженную на (1/5). Вычитаем из строки 4 строку 3, умноженную на (2/17). Вычитаем из строки 5 строку 3, умноженную на (2/17). Вычитаем из строки 5 строку 4, умноженную на (3/37).
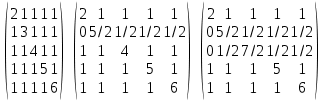
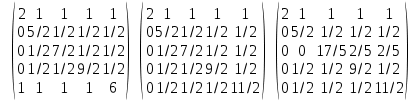
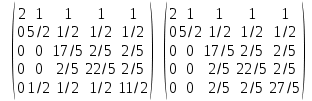
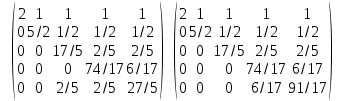
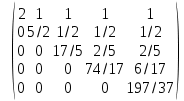
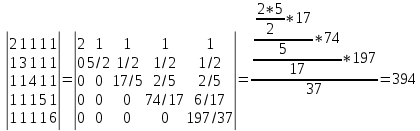
Найдем определитель матрицы путем разложения по первой строке:
