Файл: Курс таырыбы Векторлы алгебра элементтері. Сабаты таырыбы 1. Жазытытаы жне кеістіктегі векторлар.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 44
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Курс тақырыбы 1.1. Векторлық алгебра элементтері.
Сабақтың тақырыбы №1. Жазықтықтағы және кеңістіктегі векторлар.
Кесінді- ол кесінді ұштары болып келетің екі нүкте арқылы сипатталады. Егер екі нүктенің қайсысы- басы, қайсысы- соңы деген сқрақ туындаса, онда бағытталған кесінді ұғымы пайда болады. Анықтама: Бағытталған кесіндівектордеп аталады..
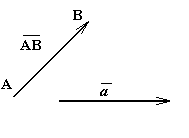
Вектор А – басы, ал В – соңы болатын АВ немесе a әрпімен белгіленеді.
Бастапқы және соңғы нүктелер арасындағы қашықтық вектор ұзындығ деп аталады. Оны белгілеу үшін модуль белгісін қолданады.
Ұзындығы бірге тең вектор орт деп аталады, егер нөлге тең болса, онда нөлдік вектор деп аталады. Нөлдік вектордың бастапқы және соңғы нүктелері бетттеседі және белгілі бағыты болмайды.
Бір түзудің бойынд жататын немесе параллель түзулер бойындағы векторлар коллинеар векторлар д.а.
Векторлар компланар векторлар д.а., егер олар бір жазықтықта немесе паралелль жазықтықтарда орналасса.
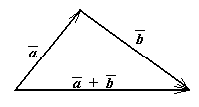
Екі вектор тең д.а., егер олар: 1) коллинеар; 2) ұзындықтары тең; 3) бағыттас болса.
Кеңістіктегі
Действительно, если система векторов
базис деп кез- келген реттелген компланар емес үш векторды айтады.
Теорема: Екі векторды қосқанда олардың координаталары қосылады. Векторды санға көбейтсе, вектор координаталары сол санға көбейтіледі.
Егер
Действительно, если
екі вектор арасындағы бұрыш тік болса, онда ол векторлар ортогональ векторлар д.а.
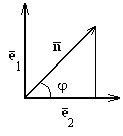 -векторының
-векторының Векторлар проекциясы мынадай қасиеттерге ие:
1.
-
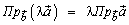 (вектордың санға
(вектордың санға
көбейтіндісінің проекциясы вектор проекциясының сол санға көбейтіндісіне тең).
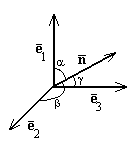 cosα, cosβ, cosγ шамалар бағыттаушы косинустар д.а.
cosα, cosβ, cosγ шамалар бағыттаушы косинустар д.а. Векторларға қолданылатын амалдар.
-
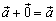

-
кез- келген вектор үшін оған қарама- қарсы
вектор үшін оған қарама- қарсы
 және
және 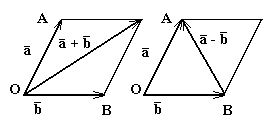
1)
Векторлардың скаляр және векторлық көбейтінділері
Екі вектордың скаляр көбейтіндісі деп ол векторлар ұзындықтары мен екеуінің арасындағы бұрыш косинусына көбейтіндісіне тең санды айтады.
Скаляр көбейтіндінің мынадай қасиеттері бар:
-
Скаляр көбейтінді көбейгіштердің біреуі нөлдік
вектор болғанда немесе екі вектор ортогональ болғанда ғана нөлге тең.
-
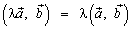 .
.
Действительно, пусть
Скаляр көбейтінді мына формулаларда қолданылады
1.
-
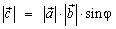 , мұндағы φ –
, мұндағы φ –  және
және  векторлар арсындағы бұрыш;
векторлар арсындағы бұрыш; -
 векторы
векторы 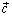 векторына,
векторына, 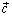 векторы
векторы  векторына ортогональ;
векторына ортогональ;
Теорема:Егер екі вектордың векторлық көбейтіндісі нөлге тең болса, онда ол векторлар коллинеар векторлар.
Теорема: Длина (модуль) Векторлардың векторлық көбейтіндісінің ұзындығы осы екі вектор арқылы тұрғызылған параллелограмм ауданына тең.
Действительно, можно заметить, что