Файл: Курс таырыбы Векторлы алгебра элементтері. Сабаты таырыбы 1. Жазытытаы жне кеістіктегі векторлар.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 45
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Векторлық көбейтіндінің келесі қасиеттері бар:
-
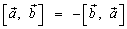 ;
;
Действительно, из определения следует, что модуль векторного произведения не зависит от порядка сомножителей. Точно так же вектор
-
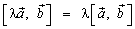 ;
;
Если φ - угол между векторами
-
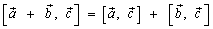
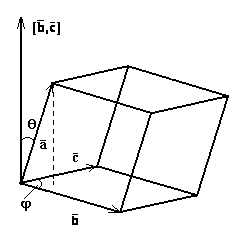 ;
;
Если
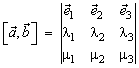 .
.Справедливость теоремы следует из предыдущих формул при учете примеров в начале раздела. Чтобы избежать постоянных замечаний об ориентации базиса, мы будем считать, что базис выбирается всегда правый.
Векторлық көбейтінді мынадай екі есепті шешуге қолданылады:
-
Екі вектор тиісті болатын жазықтыққа перпендикуляр векторды табу -
Параллелограмм ауданын
табу S .
Теорема: Векторлардың аралас көбейтіндісі үш векторға тұрғызылған параллелепипед көлеміне тең. Оның таңбасы оң болады, егер үш вектор оң үштік, ал теріс, егер сол үштік болса.
Теорема: Үш вектордың аралас көбейтіндісі нөлге тең болса, онда ол векторлар компланар болады. произведение обладает следующими свойствами:
Мысал. Төбелері А(0, -3, -1), В(3, 3, 2), С(1, 0, -3) және
D(2, -1, 1) нүктелерінде болатын пирамида көлемін табу керек.
Отметим, что объем пирамиды ABCD пирамида көлемі осы AB, AC және AD векторларға тұрғызылған параллелепипед көлемінен 6 есе аз. Ол векторлар координаталарын табайық:
AB = {3,6,3}, AC = {1,3,-2}, AD = {2,2,2}. Онда AB AC AD =

Пирамида көлемі 18:3 =6.
Оқытушы: Слямова Г.Б