Файл: Лабораторная работа 1 статистический ряд и его обработка при управлении качеством электронных средств.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 33
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Гистограмма распределения обычно строится для интервального изменения значения параметра. Для этого на интервалах, отложенных на оси абсцисс, строят прямоугольники (столбики), высоты которых пропорциональны частотам интервалов. Гистограмма интервального ряда изображена на рисунке 2, где по оси ординат отложены абсолютные значения частот.
Для построения кумулятивной кривой по данным выборки таблицы 1, контрольный лист которой в форме Б представлен в таблице 3, отложим по оси абсцисс 14 значений параметра качества: 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203 вольта (рисунок 3), а по оси ординат 80 значений от 0 до 80 через каждые 5 значений: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, т.е. столько сколько изделий в выборке. Построив оси координат, наносим сетку (рисунок 3). Далее в столбике со значением 190 отложим горизонтальную черту на высоте, равной 1, т.е. столько раз повторяется значение параметра в 190 вольт. Затем в столбике со значением 191 отложим горизонтальную черту на высоте, равной 2. Цифра 2 получается как сумма числа повторений 191 и числа повторений 190. Далее в столбике со значением 192, отложим горизонтальную черту на высоте 4 единицы. Цифра 4 получается как сумма числа повторений значений 192 (2 значения) и предыдущего значения (2 значения). Затем отложим горизонтальную черту в столбике со значением 193 на высоте 7 единиц. Цифра 7 получается как сумма числа повторений значения 193 (3 значения) и предыдущего значения, равного 4 единицам. Дальше, отложим горизонтальную черточку в столбике со значением 194 на высоте 13 единиц. Эта цифра 13 получается как сумма числа повторений значений 194 (6 единиц) и предыдущего значения, равного 7 единицам. Затем, отложим горизонтальную черточку в столбике со значением 195 на высоте 25 единиц. Эта цифра 25 получается, как сумма числа повторений значений 195 (12 раз) и предыдущего значения, равного 13 единицам. Аналогичным образом, продолжаем откладывать горизонтальные черточки для столбиков со значениями 196, 197, 198, 199, 200 и так далее до 203. Горизонтальная черточка в столбике со значением 202 будет на высоте 79 единиц, а со значением 203 единицы на высоте 80 единиц.
Следует отметить, что кумулятивная кривая в начале и в конце графика нарастает медленно (угол наклона близок к горизонтальному) т.к. прирост значений в начале и в конце гистограммы мал. А в центральной части кумулятивной кривой прирост значений большой, поэтому кумулятивная кривая идет круче.
Заметим, что площадь, ограниченная полигоном и осью абсцисс, в том случае, если по оси ординат отложены значения относительных частот, также равна единице. Как видно из рисунка 2, кривая теоретических распределений имеет идеальную форму, к которой стремится реальный полигон, и она играет важную роль в теоретических исследованиях. Кстати, кривая (рисунок 2) похожа на кривую плотности распределения, которую называют кривой нормального распределения. Для выяснения того, соответствует ли данное распределение результатов измерения нормальному распределению, используют специальную вероятностную бумагу, называемую нормальной вероятностной бумагой. Представление данных по такой бумаге, осуществляется следующим способом. Кумулятивная кривая строится как для дискретного, так и для непрерывного изменения значений параметра. При этом следует отметить, что накопленные частоты (частости) интервального ряда относятся не к серединам интервалов, а к верхним границам каждого из них. Высота последней ординаты соответствует объему наблюдений всего ряда, или 100%. Зависимость на рисунке 3 представляет собой полигон, построенный на основе таблиц накопленных частот, и носит название накопленного полигона (рисунок 3), а ломаная кривая представляет собой кумулятивную кривую. (Обратите внимание, как в данном случае соединены отрезки ломаной). Кумулятивная кривая имеет более плавный характер изменения, чем гистограмма или полигон частот, ибо накопление приводит к сглаживанию. Значения накопленных частот, соответствующих одно-, двух- и трехкратному стандартному отклонению значения параметра качества от среднего значения исследуемого статического наносят на нормальную вероятностную бумагу.
2.7. Численные методы представлениястатистического ряда
Графические методы представления однородной совокупности, давая более наглядную картину характера распределения параметра качества, чем таблицы, в то же время не могут быть применены для достоверной оценки качества продукции по результатам контрольной выборки. В этом случае удобно представить статистический материал не графически, а числовыми значениями, которые до некоторой степени отражают существенные характеристики статистического ряда — характеристики положения и рассеивания случайной величины.
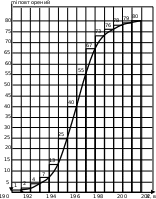
Рисунок 3 – Кумулятивная кривая
Важнейшей характеристикой положения случайной величины является средняя арифметическая величина наблюдаемых значений параметра качества (или просто средняя), которую для характеристики выборки будем называть, выборочной средней арифметической и обозначать через
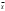. Если в результате п измерений получены значения x1,x2, ..., хn, то
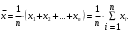(3)В случае статистического ряда (когда значению параметра соответствует какая-либо частота) средняя арифметическая величина вычисляется по формуле:
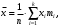(4)где
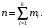
В этом случае среднюю называют средней взвешенной.
Другая статистическая характеристика рассеивания наблюдаемых значений показывает, как тесно группируются отдельные значения вокруг средней арифметической или как они рассеиваются вокруг этой средней. Так как алгебраическая сумма отклонения отдельных значений xi от средней арифметической x равна нулю и непригодна в качестве меры рассеивания, за меру рассеивания принимают сумму квадратов отклонений отдельных значений от средней арифметической, делённую на число наблюдений, уменьшенное на единицу. Эту меру называют выборочной дисперсией и обозначают через s2. Для простой статистической совокупности
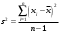(5)При наличии частот mi
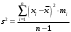(6)где
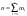.Вместо выборочной дисперсии s2 часто применяют выборочное стандартное отклонение s. Оно имеет ту же размерность, что и средняя арифметическая
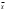. Выборочное стандартное отклонение для простой статистической совокупности и при наличии частот определяется соответственно по следующим формулам:
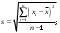(7)
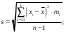(8)Отношение стандартного отклонения к средней арифметической, выраженное в процентах, называют коэффициентом вариации V:
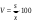(9)Коэффициент вариации, который также используется как статистическая характеристика рассеивания, показывает относительное колебание отдельных значений около средней арифметической. Коэффициент вариации, являясь безразмерным, удобен для сравнения рассеивания случайной величины с её средним значением.
3. ВОПРОСЫ К ДОМАШНЕМУ ЗАДАНИЮ
3.1. Что понимается под статистическим рядом и какие его разновидности Вам известны?
3.2. Приведите пример дискретного и непрерывного изменений случайной величины.
3.3. Как составляется и в дальнейшем заполняется контрольный лист?
3.4. Какие числовые характеристики статистического ряда Вам известны?
3.5. В чем отличие генеральных и выборочных характеристик?
3.6. Поясните порядок построения наиболее распространенных графиков представления статистического ряда.
3.7. Что такое выборка?
3.8. Перечислить и охарактеризовать виды выборок.
3.9. Что понимается под абсолютной и относительной частотами?
3.10. Пояснить способы объединения данных в интервальный ряд.
4. ЛАБОРАТОРНОЕ ЗАДАНИЕ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ЕГО ВЫПОЛНЕНИЮ
4.1. По выданному преподавателем номеру варианта получить статистические данные измеренного параметра качества электронного средства.
4.2. Построить упорядоченный статистический ряд данных и контрольный листок (по формам А и Б).
4.3. Построить интервальный ряд данных.
4.4. Построить полигон и гистограмму частот интервального ряда.
4.5. Построить кумулятивную кривую частот интервального ряда.
4.6. Вычислить среднюю арифметическую величину, медиану, моду и размах статистического ряда данных.
4.7. Вычислить выборочную дисперсию, стандартное отклонение и коэффициент вариации.
5. УКАЗАНИЯ ПО ОФОРМЛЕНИЮ ОТЧЕТА
В отчёте по лабораторной работе №1 указывается следующее:
а) наименование лабораторной работы и её цель;
б) результаты выполнения домашнего задания;
в) ход и результаты выполнения лабораторного задания, где приводятся исходные данные, все расчёты, проводится анализ, делаются выводы, в которых указываются приобретенные при выполнении лабораторной работы знания и навыки.
Студент отчитывается о выполненной и оформленной лабораторной работе на следующем занятии.
6. КОНТРОЛЬНЫЕ ВОПРОСЫ
6.1. Как строится упорядоченный статистический ряд?
6.2. Какие данные содержит контрольный листок, как он заполняется и как используется при управлении качеством?
6.3. Как строится и когда используется полигон и гистограмма частот значений измеренного параметра?
6.4. Что такое кумулятивная кривая и как она строится?
6.5. Как вычисляются средняя арифметическая величина, медиана, мода, размах, выборочная дисперсия, стандартное отклонение и коэффициент вариации? Для каких целей они используются?