Лабораторная работа № 3
«Теплоемкость идеального газа»

Цель работы:

• 
  Знакомство с теплоемкостью идеального газа в изохорическом и изобарическом процессах.
  
• 
  Экспериментальное подтверждение закономерностей изопроцессов.
  
• 
  Экспериментальное определение количества степеней свободы и структуры молекул газа в данной модели.
  

КРАТКАЯ ТЕОРИЯ:

Идеальным называется такой газ, в котором считается, что собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда, в котором он находится, силы взаимодействия между молекулами газа отсутствуют, а столкновения между молекулами газа абсолютно упругие.

Внутренней энергией газа U называется сумма кинетической энергии хаотического (теплового) движения всех молекул газа и энергии взаимодействия молекул газа между собой. Для идеального газа внутренняя энергия – это только кинетическая энергия всех молекул газа.

Внутренняя энергия идеального газа определяется числом степеней свободы его молекул и температурой газа.

Числом степеней свободы i механической системы называется количество независимых величин, с помощью которых может быть однозначно задано положение системы в пространстве.

средняя кинетическая энергия молекулы:



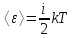
где i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы:



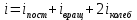
Теплоемкостью тела называется величина, равная количеству теплоты, которое нужно сообщить телу, чтобы повысить его температуру на 1 К.

Удельная теплоемкость вещества – величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 К:

.

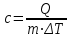Молярная теплоемкость вещества – величина, равная количеству теплоты, необходимому для нагревания 1 моля вещества на 1 К:

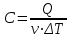, откуда .

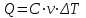Различают теплоемкости газа при изохорном и изобарном процессах.

---

1. Молярная теплоемкость газа при изохорном процессе .

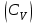Для изохорного процесса первое начало термодинамики:

.

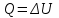Следовательно 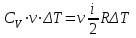, откуда .

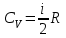2. Молярная теплоемкость газа при изобарном процессе .

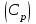Для изобарного процесса первое начало термодинамики:

.

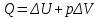Так как для изобарного процесса ,

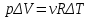то ,

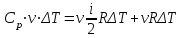откуда .

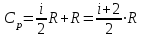Рассмотрим теплоемкость идеального газа в изопроцессах.

1. 
   Адиабатический.
   

В адиабатическом процессе теплообмена с окружающей средой не происходит, т.е. 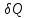=0. Следовательно, теплоемкость идеального газа в адиабатическом процессе также равна нулю: С 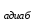=0.

2. 
   Изотермический.
   

В изотермическом процессе постоянна температура, т.е. dT = 0. Следовательно, теплоемкость идеального газа стремится к бесконечности: .

3. 
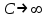   Изохорный.
   

В изохорическом процессе постоянен объем, т.е. δV = 0. Элементарная работа газа равна произведению изменения объема на давление, при котором происходит изменение (δA = δVP). Первое начало термодинамики для изохорического процесса имеет вид:

dU = δQ = C 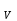ΔT.

А для идеального газа



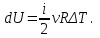
Таким образом

,

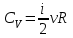где i - число степеней свободы частиц газа.

4. 
   Изобарный.
   

В изобарическом процессе (P = const):



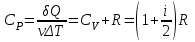
ВЫПОЛНЕНИЕ РАБОТЫ

Результаты измерений и расчетов:

---

1. Одноатомный газ: V₀= 40 · 10^-3 м³, p₀= 140 · 10³ Па, ν =1,8 · 10^-3 кмоль



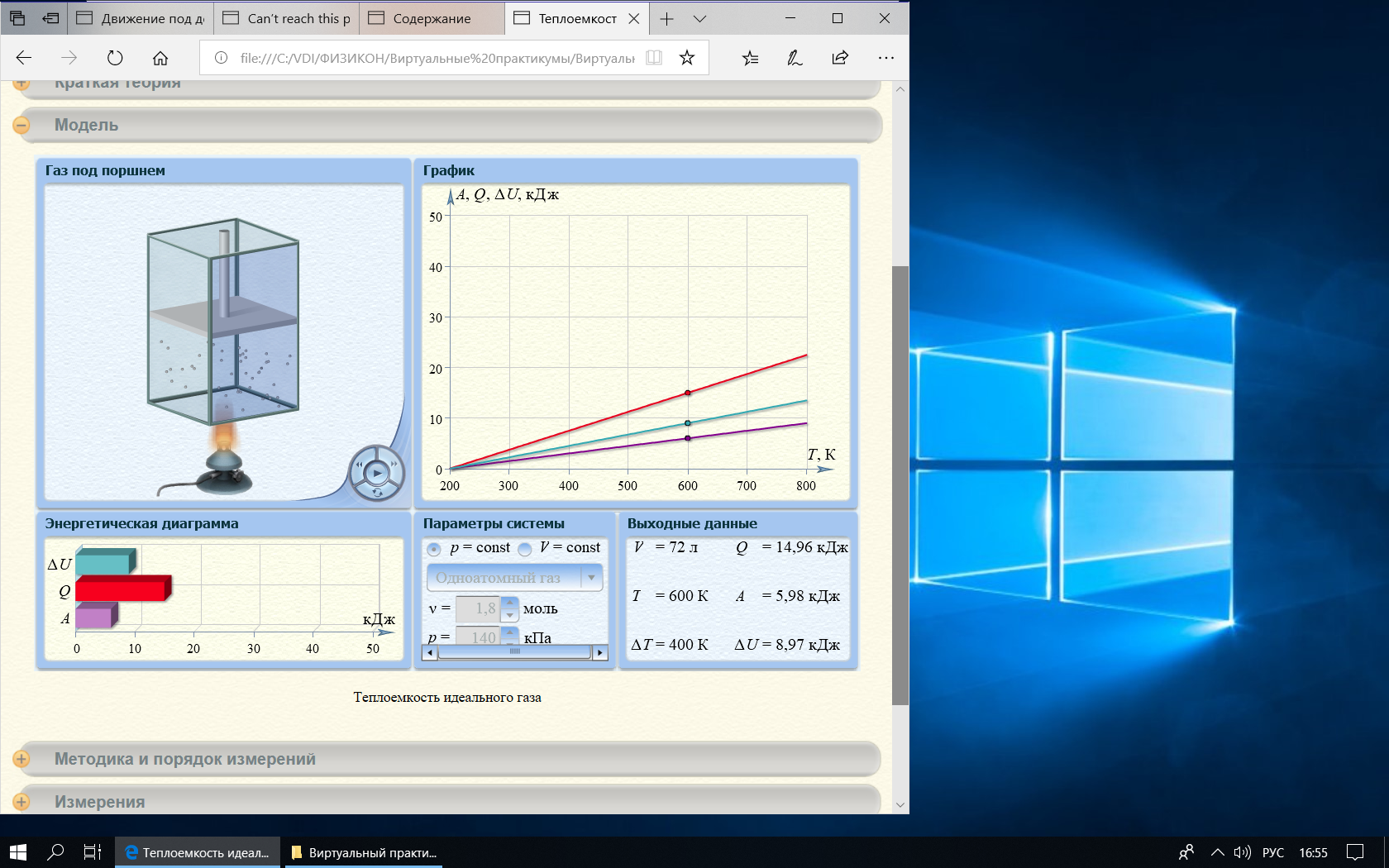
Таблица 2

Т, К	300	400	500	600	700	800
QV,кДж	2,24	4,49	6,73	8,97	11,22	13,46
Т, К	295	404	495	600	704	800
Qр,кДж	3,55	7,63	11,03	14,96	18,85	22,44

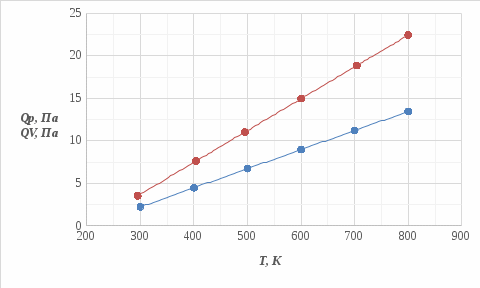
Графики зависимостей Q_V=f(T) и Q_p=f(T) для одноатомного газа.



Определение C_p теплоемкости и c_p молярной теплоемкости газа при постоянном давлении:





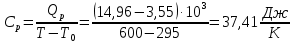
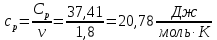
Определение C_V теплоемкости и c_V молярной теплоемкости газа при постоянном объеме:





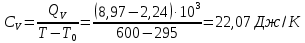
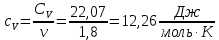
Определение γ постоянной адиабаты:



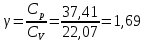
Определение iчисла степеней свободы молекул газов:



2. Двухатомный газ: V₀= 40 · 10^-3 м³, p₀= 140 · 10³ Па, ν =1,8 · 10^-3 кмоль



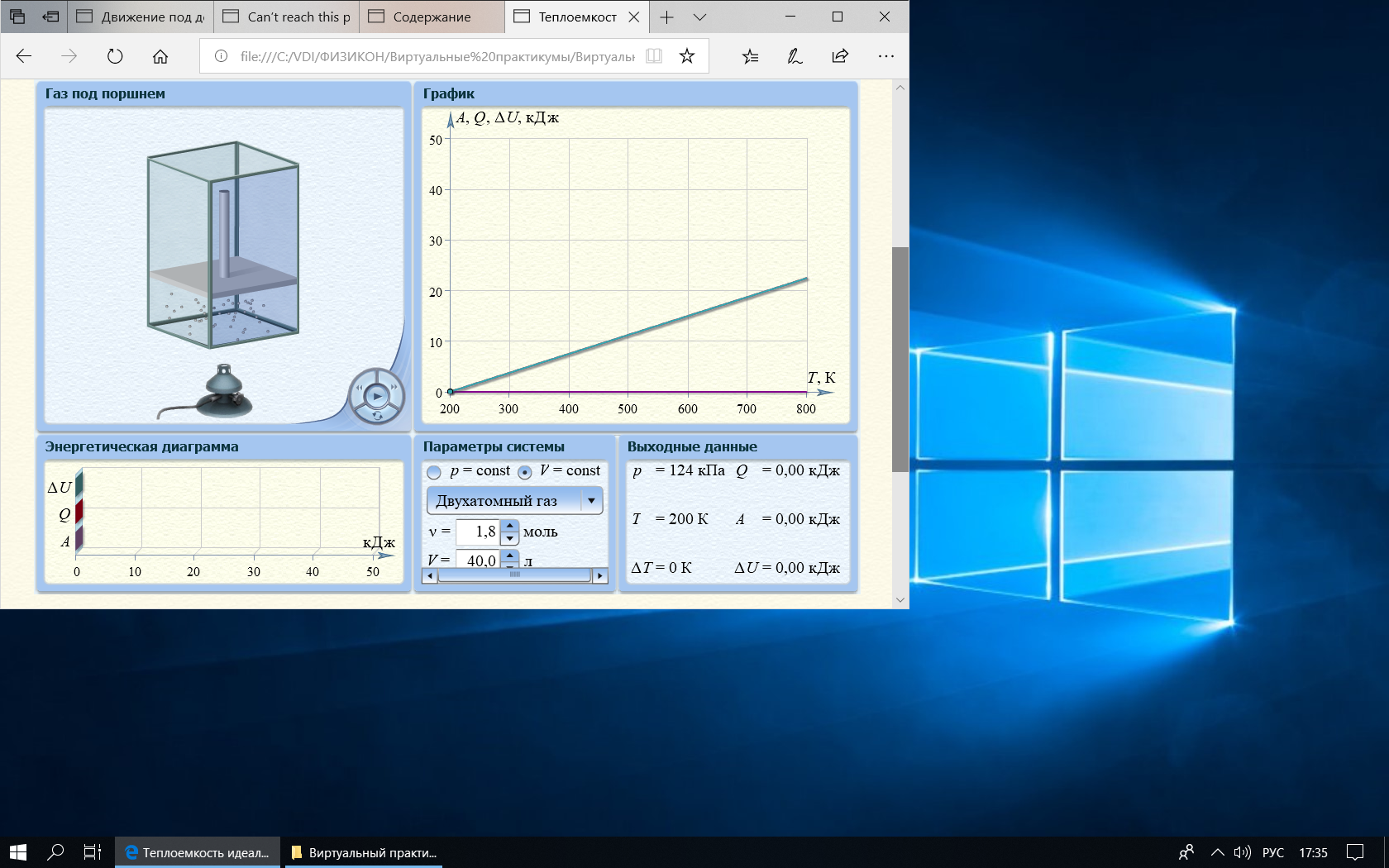
Таблица 3

Т, К	300	395	500	605	700	795
QV,кДж	3,74	7,29	11,22	15,14	18,70	22,25
Т, К	300	405	505	605	700	800
Qр,кДж	5,24	10,73	15,97	21,20	26,18	31,41

---

Графики зависимостей Q_V=f(T) и Q_p=f(T) для двухатомного газа:



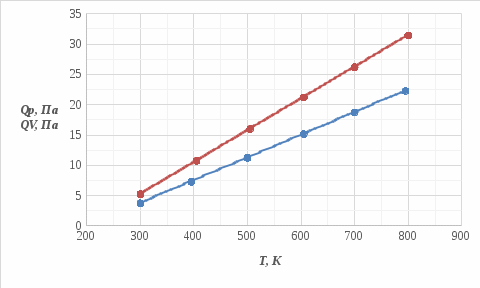
Определение C_p теплоемкости и c_p молярной теплоемкости двухатомного газа при постоянном давлении:




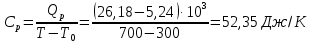
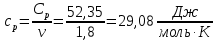
Определение C_V теплоемкости и c_V молярной теплоемкости двухатомного газа при постоянном объеме:





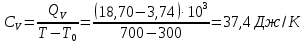
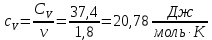
Определение γ постоянной адиабаты:



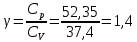
Определение iчисла степеней свободы молекул газов:



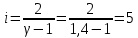
3. Трехатомный газ: V₀= 40 · 10^-3 м³, p₀= 140 · 10³ Па, ν =1,8 · 10^-3 кмоль



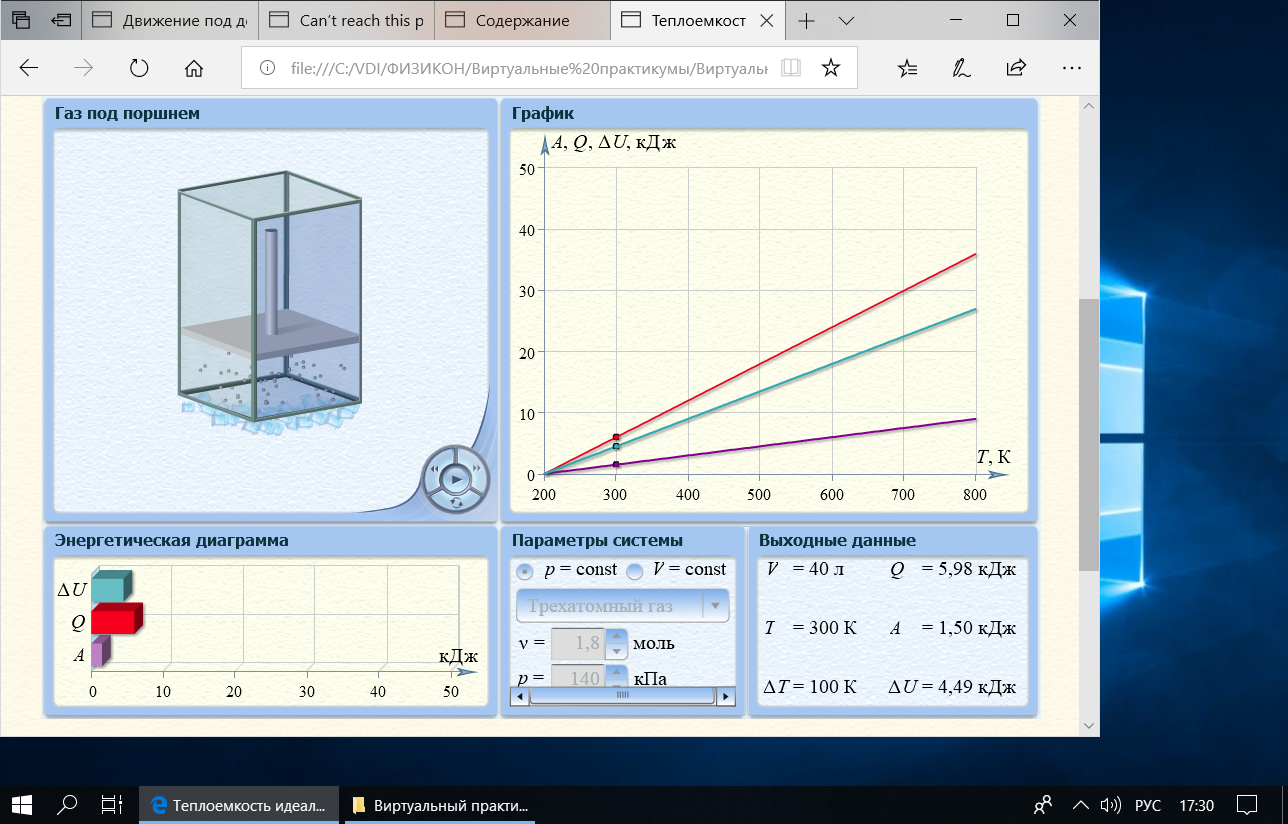
Таблица 4

Т, К	300	395	495	605	695	800
QV,кДж	4,49	8,75	13,24	18,17	22,21	26,92
Т, К	300	395	495	600	700	800
Qр,кДж	5,98	11,67	17,65	23,93	29,92	35,90

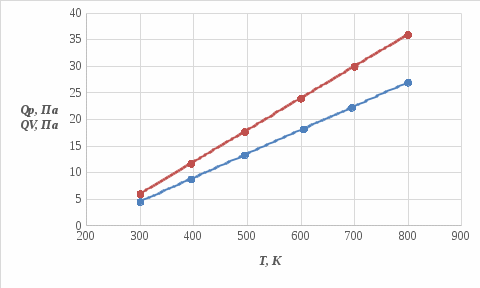
Графики зависимостей Q_V=f(T) и Q_p=f(T) для трехатомного газа:



Определение C_p теплоемкости и c_p молярной теплоемкости трехатомного газа при постоянном давлении:

---

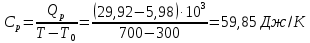
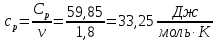
Определение C_V теплоемкости и c_V молярной теплоемкости трехатомного газа при постоянном объеме:





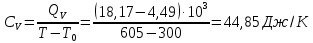
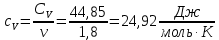
Определение γ постоянной адиабаты:



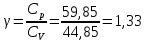
Определение iчисла степеней свободы молекул газов:



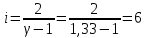
Вывод: в работе определены теплоемкости для идеального газа в изохорном и изобарном процессах. Построены графики зависимостей теплоты переданной одноатомному, двухатомному и трехатомному газу. Полученные графики имеют вид прямой, проходящей через начало координат и качественно совпадают с соответствующей формулой 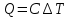. По результатам измерений и расчетов были определено число степеней свободы газа и постоянная адиабаты.

Для одноатомного газа теплоемкост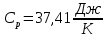и

и ,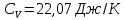

Молярные теплоемкост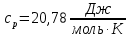и и .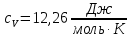

Число степеней свободы газа и постоянная адиабаты



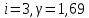
Для двухатомного газа теплоемкости





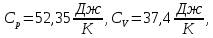
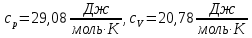
Число степеней свободы газа и постоянная адиабаты



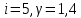
Для трехатомного газа теплоемкости





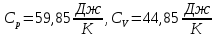
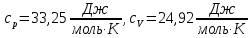
Число степеней свободы газа и постоянная адиабаты



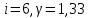
Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании.

---

Смотрите также файлы

• 1. в методике idef3 используются диаграммы.docx

• Правила соревнований любого вида единоборств.docx

• Программа среднего профессионального образования 44. 02. 03. Педагогика дополнительного образования (в области технического творчества) Дисциплина Математика Практическое занятие 2.doc

• Политехнический колледж.docx

• Задание 14Студента команды ат03 Мягченко Илья Дмитриевич преподаватель Ламоткин А. Е.pdf