ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 17
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Технологическая карта урока алгебры и начал математического анализа
ФИО: Калачева Наталья Федоровна
Номер группы: МДМ-117
Класс – 10
Тема урока – Показательные уравнения
Цель урока: сформировать представление о показательных уравнениях, освоить основные способов решения показательных уравнений.
Задачи:
-
Обучающие – введение определения показательных уравнений, формирование основных способов решения простейших показательных уравнений; формирование умения и навыки правильно определять и применять данные способы при решении конкретных показательных уравнений. -
Развивающие – развитие мышления, различных видов памяти, внимания, речи, умения делать обобщения и выводы, умение работать с новым материалом, структурировать полученные знания; выработка умений решения показательных уравнений; -
Воспитательные – воспитывать культуру общения, умение работать в коллективе, взаимопомощи, воспитывать навыки самостоятельности и саморазвития, взаимоконтроля.
Тип урока: открытия новых знаний
Планируемые результаты:
Личностные: понимание значения применение различных способов решения показательных уравнений; интерес к изучению темы и желание применять приобретённые знания и умения в практической деятельности; умение осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований.
Предметные: знание определения показательных уравнений, систематизированные представления о способах решения показательных уравнений; умения решать показательные уравнение с применением различных способов, закрепление свойств показательной функции в процессе решения показательных уравнений;
Метапредметные: умение применять на практике знания способов решения показательных уравнений; применение данного материала при изучении дисциплин естественнонаучного цикла, формирование умения осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований.
Формы работы учащихся: фронтальная, индивидуальная.
Дидактические средства: Колягин, Ю. М. Алгебра и начала математического анализа. 10 класс : учебник для общеобразовательных учреждений : базовый и профильный уровни / Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин; под ред. А. Б. Жижченко. – Москва : Просвещение, 2011. – 368 с. – ISBN 978-5-09-025401-4.; Шабунин, М. И. Алгебра и начала математического анализа. 10 класс. Дидактические материалы. Базовый и углубленный уровни / М. И. Шабунин, М. В. Ткачева, Н. Е. Фёдорова. – Москва : Просвещение, 2021. – 142 с. – ISBN 978-5-09-070944-6.презентация «Показательные уравнения», карточки для самостоятельной работы, оценочный лист.
Оборудование: персональный компьютер (ПК) учителя, мультимедийный проектор, экран.
Технологическая карта урока
| Этап, количество минут | Виды работы, формы, методы, приемы | Содержание педагогического взаимодействия | Слайд презентации (Запись на доске, в тетрадях) | УУД | |
| Деятельность учителя | Деятельность учащихся | ||||
| Организационный момент. Мотивация (самоопределения) к учебной деятельности (2 мин.) | Эмоциональный настрой, самоопределение к деятельности. | Приветствует обучающихся, проверяет готовность класса, производит проверку отсутствующих. Организует внимание учеников. Здравствуйте ребята. Я рада снова видеть вас на уроке. Эпиграфом к нашему уроку станут слова: «Уравнения – это золотой ключ, открывающий все математические сезамы» - Я желаю вам сегодня на уроке убедиться в справедливости этих слов С. Коваля Проводит инструктаж по работе с листом самооценки: На столах у вас лежат маршрутные листы (Приложение 1). Подпишите их. В течение урока вы постарайтесь оценить себя и одного из одноклассников, по критериям, которые указаны в маршрутных листах. | Приветствие учителя. Подготовка класса к работе. Участие в беседе. Имеют представление о работе с листом оценки. | Слайд 1  | Коммуникативные: умение выражать свои мысли, строить высказывания в соответствие с задачами коммуникации. Регулятивные: целеполагание, мотивация к обучению и целенаправленной познавательной деятельности. Личностные: самоопределение; |
| Актуализация и фиксирование индивидуального затруднения в пробном действии (4 мин.) | Словесный (беседа), фронтальная форма, организация проблемной ситуации. | Начинает урок с проверки домашнего задания. Выводит правильные ответы на слайд. - Проверим выполнение домашнего задания. У кого решение правильно ставим плюс возле задания, у кого неверно - минус. Решение задания под номером 11 озвучит (ученик)… - Спасибо, теперь проверим правильность выполнения задания под номером 14 Решение задания озвучит (ученик).... - Итак, все верно, проверим последнее задание под номером 15. Посмотрите на слайд и сравните полученные вами графики с графиками на слайде. Поставьте плюс если задание выполнено верно и минус если выполнено неверно. - Поставьте в конце домашнего задания себе оценку. Критерий самооценки: "5"- верно выполнены все примеры, "4"- допущена только одна ошибка, "3"- допущено 2 и 3 ошибки. Актуализирует знания по пройденной теме. Учитель по очереди осуществляет фронтальный опрос учащихся.
1. Какую функцию называют показательной? 2. Какие их перечисленных ниже функций являются показательными: 1) 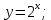 2) 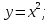 3) 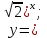 4) 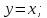 5) 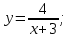 6) 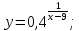 7) 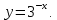 3. Назовите основные свойства показательной функции. 4. Выберите возрастающие функции: 1) 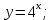 2) 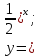 3) 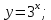 4) 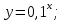 5) 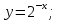 6) 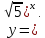 5. Укажите область определения функции 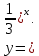 Задание на повторение свойств степени. Вычислите устно: 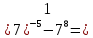 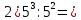 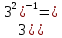 4) 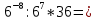 5) 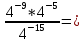 Предлагает решить задание записанные на доске. Контролирует выполнения задания, осуществляет проверку правильности решения заданий. Предлагает выбранному ученику предъявить свое решение классу. При решении задания учащиеся встретятся с затруднением. Задание. Назовите виды уравнений. Решите их. 1) 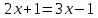 ; ;2) 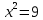 ; ;3) 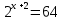 ; ;4) 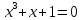 ; ;5) 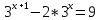 ; ;6) 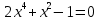 ; ;7) 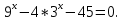 | Выбранные или изъявившие желание ученики комментируют выполненные задания. Ответы: №11 Найти область определения функции. 1) 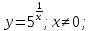 D(f)= 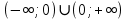 . .2) 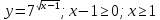 D(f)= 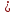 . .3) 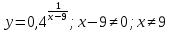 D(f)= 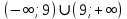 . .4) 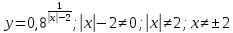 D(f)= 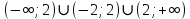 . .№14 Найти наибольшее и наименьшее значения функции: 1) 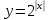 , при , при 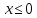 убывает, при убывает, при 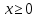 возрастает. возрастает.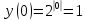 – наименьшее значение – наименьшее значение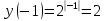 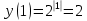 – наибольшее значение. – наибольшее значение.2) 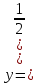 , при , при 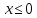 возрастает, при возрастает, при 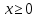 убывает. убывает.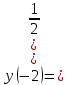 – наименьшее значение – наименьшее значение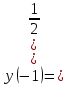 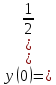 – наибольшее значение – наибольшее значение 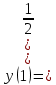 №15. Построить графики функций. 1) 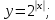 2) 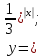 3) 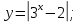 4) 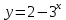 . .Отвечают на вопросы. 1. Показательной функцией называется функция вида 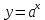 , где а – заданное число, такое, что a>0, a , где а – заданное число, такое, что a>0, a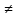 1. 1.2. Из перечисленных функций, показательными являются функции под номерами 1, 3,6,7. 3. Основные свойства показательной функции: область определения – множество всех действительных чисел; множество значение – множество всех положительных чисел; показательная функция является возрастающей на множестве действительных чисел, если a>1, и убывающей, если 0 4. Из предложенных функций возрастающими являются функции по номерами 1, 3, 6. 5. Область определения функции 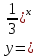 является промежуток (-1;+ является промежуток (-1;+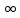 ). ).Устно выполняют предложенное учителем задание. Выходят к доске, решают примеры, записывают решения в тетрадь. Пробуют выполнить задание предложенное учителем, сталкиваются с проблемой. Не знают вид уравнений 3,5,7, не знают способы решения данных уравнений. | Слайд 2  Слайд 3  Слайд 4 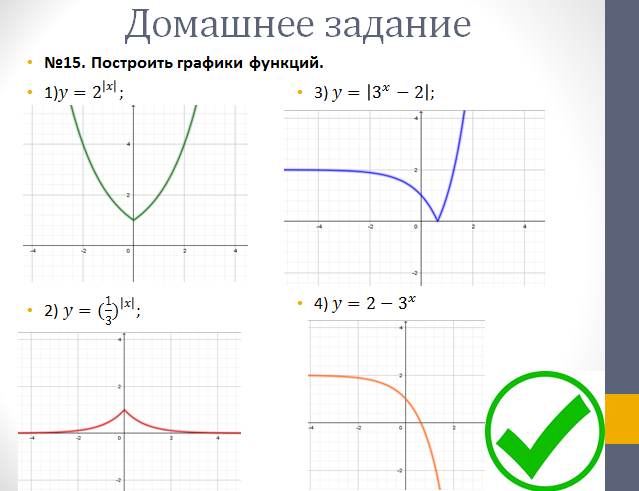 Слайд 5  Слайд 6  | Познавательные: умение структурировать знания; использование знаково-символических средств; смысловое чтение, осознанное и произвольное построение речевого высказывания в устной и письменной форме Коммуникативные: достаточно точное и полное выражение своих мыслей, учет разных мнений учащихся Регулятивные: фиксирование индивидуального затруднения, волевая саморегуляция и ситуации затруднения. Личностные: формирование навыков самоконтроля; формирование потребности в самовыражении и самореализации |
| Выявления места и причины затруднений (2 мин.) | Словесный метод (беседа), фронтальная форма, проблемный диалог | Учитель предоставляет возможность ученикам осознать, в чем именно состоит затруднение, каких знаний, умений и навыков им не хватает для решения пробного задания. Задает вопросы. Вопросы: - Получилось ли у вас полностью выполнить задание? - Что не получилось? - Почему не получилось? | В процессе рассуждений, выясняют в чем именно состоит затруднение, каких знаний, умений и навыков им не хватает для решения пробного задания. Отвечают на вопросы: - Задание выполнить полностью не получилось. - Не получилось решить уравнения под номерами 3, 5, 7. - Не получилось потому, что не знаем вид данных уравнений и их способов решения. | | Познавательные: анализ, сравнение, постановка и формулировка проблемы, построение речевого высказывания Коммуникативные: выражение своих мыслей, аргументация учет разных мнений, координирование в сотрудничестве разных позиций Регулятивные: волевая саморегуляция в ситуации затруднения Личностные: адекватно реагировать на трудности и не бояться сделать ошибку. |
| Построение проекта выхода из создавшейся ситуации (5 мин.) | Словесный метод (беседа). Фронтальная форма, задавание проблемных вопросов. | Подведение к формулированию темы и целей урока. - Исходя из этого и из того, что у вас возникли трудности при выполнении задания попробуем сформулировать тему нашего урока и поставим цели на урок. - Обратимся еще раз к данным уравнениям, неизвестная переменная в уравнениях 2, 4, 6 стоит в основании степени (слайд 6). - Где стоит неизвестная переменная в уравнениях 3, 5, 7? - Отсюда мы можем сделать вывод к какому виду относятся данные уравнения? Ваши варианты? -Верно, итак, какова тема сегодняшнего урока? - Правильно! Тема сегодняшнего урока: «Показательные уравнения» (слайд 7) -Какие цели вы поставите на урок? -Открываем тетради, записываем число, «Классная работа» Тему урока: «Показательные уравнения». | Слушают учителя. Отвечают на вопросы учителя. -Неизвестная переменная в данных уравнениях стоит в показатели степени. -Возможно, данные уравнения являются показательными. Формулируют тему урока. -Тема сегодняшнего урока «Показательные уравнения» Формулируют цели урока: - Цель урока: овладение основными способами решения показательных уравнений Делают соответствующие записи в тетрадь. | Слайд 6  Слайд 7  Запись в тетради: Число. Классная работа. Тема: Показательные уравнения. | Познавательные: умение структурировать знания, использование знаково-символическихсредств; смысловое чтение, осознанное и произвольное построение речевого высказывания в устной и письменной форме Коммуникативные: на основе выбранного метода выдвинуть и обосновать гипотезу; учет разных мнений учащихся Регулятивные: осознание того, что уже освоено и что еще подлежит усвоению; целеполагание Личностные: способность к волевому усилию; осознание смысла учения и понимание личную ответственность за будущий результат |
| Реализация построенного проекта (10 мин.) | Частично-поисковая деятельность, фронтальная работа. | Предлагает учащимся совместно вывести способы решения показательных уравнений. Для этого сначала проговаривает теоретический материал, после с помощью примеров совместно с учащимися выводит алгоритм. (слайд 8) -Решение показательных уравнений часто сводится к решению уравнения 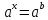 , где а>0, а , где а>0, а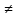 1, х - неизвестное. 1, х - неизвестное. -Это уравнение решается с помощью свойства степени, состоящего в том, что степени с одинаковым основанием а>0, а 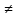 1 равны тогда и только тогда, когда равны их показатели. Это вам уже знакомо. 1 равны тогда и только тогда, когда равны их показатели. Это вам уже знакомо.Рассмотрим несколько примеров показательных уравнений, другими словами уравнений, в которых неизвестное содержится в показателе степени (слайд 9). Выводит на слайд примеры уравнений. Совместно с учащимися решает их. - Итак, нам необходимо решить следующие показательные уравнения: 1) 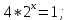 -Попробуем свести данное уравнение к виду 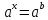 . .-Запишем правую и левую часть в виде степени с основанием 2. -Тогда какой вид примет наше уравнение? -Верно. Используем свойство степени в левой части уравнения. Как умножить степени с одинаковыми показателями? -Значит, какой вид примет уравнение? -Мы свели исходное уравнение к виду 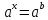 -Как решается данное уравнение? Прочитайте еще раз способ решения данного уравнения в учебнике на странице 216. -Что отсюда следует для нашего уравнения? - Значит, чему будет равен х? - Верно! Решим следующее уравнение: 2) 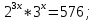 -Попробуем свести данное уравнение к виду 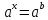 . .-Рассмотрим левую часть уравнения. Как можно ее преобразовать? -Правильно. Значит, как запишем наше уравнение? -Верно. Как еще можно преобразовать левую часть уравнения? Как умножить степени с одинаковыми показателями? -Чему будет равна левая часть уравнения? -Можно ли 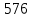 представить в виде степени с основанием 24? представить в виде степени с основанием 24?-Запишем получившейся уравнение. - Как решить данное уравнение? -Верно. Чему тогда будет равен х? -Правильно. Решим следующее уравнение: 3) 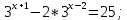 - Рассмотри левую часть уравнения. Что вы заметили? Как можно ее преобразовать? -Верно. Какой общий множитель можно вынести? -Какое уравнение получим? -Правильно. Вычислим значение выражения в скобках. Получим уравнение: 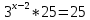 -Как можно преобразовать данное уравнение? -Верно, получим уравнение.  -Как решаем данное уравнение? -Верно. Тогда получаем уравнение: 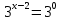 -Как решаем данное уравнение? - Верно. Чему тогда будет равен х? - Все правильно. Рассмотрим решение уравнения следующего вида: 4) 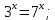 - Данное уравнение так же сводим к виду 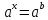 - Для этого левую часть уравнения поделим на правую, учитывая то, что 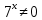 . .- Тогда какой вид примет исходное уравнение? - Как решаем данное уравнение? - Верно. Чему тогда будет равен х? - Все правильно. 5) 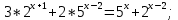 - Запишем уравнение в виде: 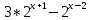 = =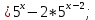 - Что можно сделать в левой и правой частях данного уравнения? - Верно. Тогда, что получается в левой и правой частях уравнения? - Упростим выражения в скобках получим: 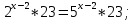 - Что возможно сделать дальше? - Верно. Получаем следующее уравнение: 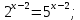 - Данное уравнение решаем как и предыдущее. Поделим левую часть уравнения на правую, так как 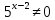 . .- Получаем: 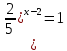 - Отсюда x-2=0, x=2. - Все понятно? Есть ли у Вас вопросы? Рассмотрим решение последнего уравнения вида: 6) 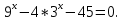 - Уравнения данного вида решаются путем сведения к квадратному уравнению с помощью замены переменной. - Какую замену можно сделать в данном уравнение чтобы перейти к квадратному уравнению? - Верно. Выполняем замену 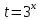 . Какое уравнение получаем? . Какое уравнение получаем?- Как решаем квадратное уравнение? - Все верно. Решая данное уравнение по теореме Виета, получаем: 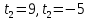 . Делаем обратную замену получаем: . Делаем обратную замену получаем: 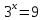 и и 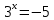 . .- Чему равен корень уравнения 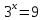 ? ? - Правильно. Уравнение 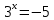 не имеет корней, так как не имеет корней, так как 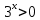 - При решении данных примеров, что вы заметили? Какие способы решения показательных уравнений вы можете выделить? Учитель озвучивает способы решения показательных уравнений: 1) Приведение к одному основанию; 2) Вынесение общего множителя за скобки; 3) Замена переменной (приведение к квадратному уравнению) (слайд 10). Раздает памятки с данными способами решения показательных уравнений и алгоритмом решения. | Слушают объяснение учителя. Записывают примеры в тетрадь. Заполняют лист самооценки. Отвечают на вопросы учителя. - Исходное уравнение примет вид: 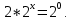 - При умножении степеней с одинаковыми основаниями, основание остается таким же, а показатели степеней складываются. - Уравнение примет вид: 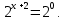 -Данное уравнение решается с помощью свойства степени, состоящего в том, что степени с одинаковыми основаниями а>0, а 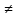 1 равны тогда и только тогда, когда равны их показатели. 1 равны тогда и только тогда, когда равны их показатели.- Отсюда следует, что уравнение 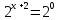 можно записать следующим образом: можно записать следующим образом:x+2=0 х=-2 Ответ: х=-2 Отвечают на вопросы учителя. - В левой части уравнения 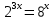 . .- Уравнение будет выглядеть следующим образом: 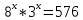 -Для того, чтобы произвести умножение степеней с одинаковыми показателями, нужно перемножить основания, а показатель степени оставить неизменным. - Левая часть уравнения равна: 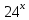 - Да, можно. 576= 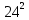 -Получили следующее уравнение: 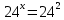 - Данное уравнение решается с помощью свойства степени, состоящего в том, что степени с одинаковыми основаниями а>0, а 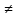 1 равны тогда и только тогда, когда равны их показатели. 1 равны тогда и только тогда, когда равны их показатели.х=2 Ответ: х=2 - В левой части уравнения можно вынести общий множитель за скобки. - Выносим общий множитель 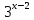 . .- Получим следующее уравнение: 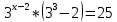 -Можно сократить на 25. - Необходимо правую часть представить в виде степени с основанием 3. - Данное уравнение решается с помощью свойства степени, состоящего в том, что степени с одинаковыми основаниями а>0, а 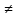 1 равны тогда и только тогда, когда равны их показатели. 1 равны тогда и только тогда, когда равны их показатели.х-2=0; х=2 Ответ: х=2 Учащиеся пытаются самостоятельно сформулировать способы решения показательных уравнений. - Исходное уравнение примет вид: 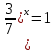 - Данное уравнение решается с помощью свойства степени, состоящего в том, что степени с одинаковыми основаниями а>0, а 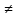 1 равны тогда и только тогда, когда равны их показатели. 1 равны тогда и только тогда, когда равны их показатели.х=0 Ответ: х=0 - В левой части уравнения можно вынести за скобки общий множитель 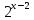 . В правой части уравнения можно вынести за скобки общий множитель . В правой части уравнения можно вынести за скобки общий множитель 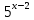 . .- Получаем: 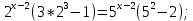 - Можно сократить уравнение на 23. - Можно 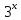 заменит на t, заменит на t,- Получаем следующее квадратное уравнение: 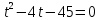 - Квадратное уравнение решаем с помощью нахождения дискриминанта или с помощью теоремы Виета. - Данное уравнение решается с помощью свойства степени, состоящего в том, что степени с одинаковыми основаниями а>0, а≠1 равны тогда и только тогда, когда равны их показатели. 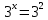 x=2 Учащиеся выдвигают свои предположения, какие способы решения показательны уравнений существуют. | Слайд 8  Слайд 9  Запись на доске и в тетради: 1. Решить уравнения: 1) 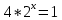 Решение: 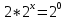 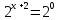 x+2=0 х=-2 Ответ: х=-2 Запись на доске и в тетради: 2) 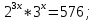 Решение: 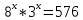 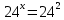 х=2 Ответ: х=2 Запись на доске и в тетради: 3) 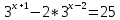 Решение: 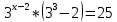 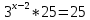  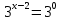 х-2=0; х=2; Ответ: х=2 Запись на доске и в тетради: 4) 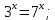 Решение: 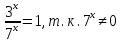 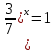 х=0 Ответ: х=0 Запись на доске и в тетради: 5) 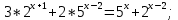 Решение: 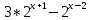 = =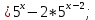 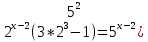 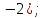 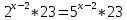 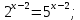 так как так как 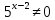 . .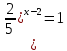 x-2=0 x=2. Ответ: х=2 Запись на доске и в тетради: 6) 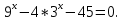 Решение: 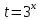 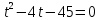 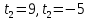 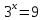 и и 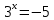 . .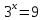 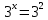 x=2 Уравнение 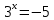 не имеет корней, так как не имеет корней, так как 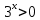 Ответ: х=2. Слайд 10 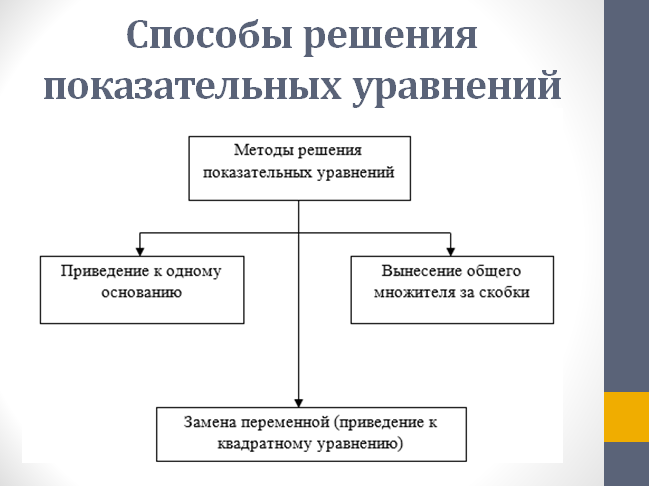 | Познавательные: построение логической цепи рассуждений, обоснование; умение использовать приобретенные знания и умения в практической деятельности. Коммуникативные: планирование учебного сотрудничества со сверстниками, инициативное сотрудничество в поиске и сборе информации, умение выражать свои мысли. Регулятивные: применение нового способа действий для решения задачи, вызвавшей затруднение Личностные: умение самостоятельно осуществлять деятельность обучения. |