ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 18
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
ФГАОУ ВО «Северо-Кавказский федеральный университет»
Невинномысский технологический институт (филиал)
Кафедра информационных систем, электропривода и автоматики
Лабараторная работа
по дисциплине
«Электрический привод»
Выполнил:
Бедаев Станислав Игоревич
студент 4 курса
группы Н-ЭЭТ-б-з-19-1
направления подготовки 13.03.02 Электроэнергетика и электротехника
заочной формы обучения
Проверил:
Колдаев А.И., доцент каф. ИСЭА
(ФИО, должность, кафедра)
Невинномысск, 2023 г.
Лабораторная работа № 1 Исследование механической части электропривода
Цель работы: Исследование динамических свойств механической части электропривода на примере трехмассовых и эквивалентных им двухмассовых расчетных схем.
Таблица 1.1 – Варианты заданий
| Вар. № | Параметры | ||||||||
| J2 | J3 | C12 | C23 | λ12 | λ23 | Mс | εmax | ω | |
| 3 | 0.3 | 0.4 | 150 | 100 | 0.2 | 0.2 | 80 | 50 | 105 |
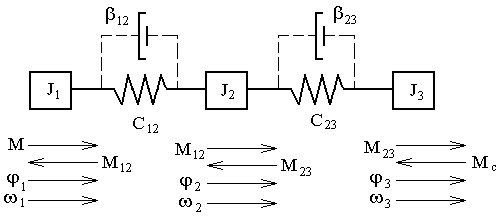
Рисунок 1.1 – Расчетная схема трехмассовой последовательной упругой системы
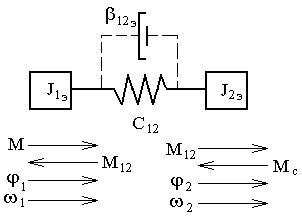
Рисунок 1.2 – Эквивалентная расчетная схема двухмассовой упругой механической системы
Математическая модель электрической части представляется следующей системой уравнений:
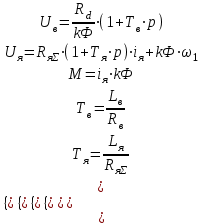(1.1)Uв =1,23
Uя =230,6
M =376,8
Tв =7,21
Tя = 13,76
Математическая модель механической части представляется следующей системой уравнений:
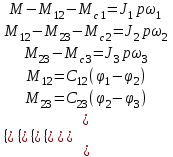(1.2)41=0,9
56=5,4
7=32,4
200=100
150=30
Структурные схемы трехмассовой и двухмассовой системы
- Структурная схема и график переходных процессов трехмассовой системы
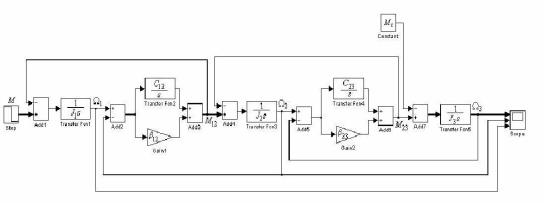
Рисунок 1.3 – Структурная схема трехмассовой системытропривод
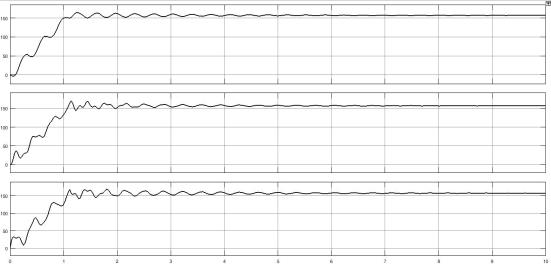
Рисунок 1.4 – Графики переходного процесса трехмассовой системы
- Структурная схема и график переходных процессов двухмассовой системы
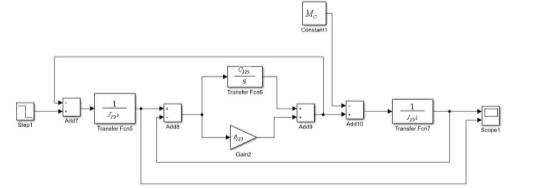
Рисунок 1.5 – Структурная схема двухмассовой системы
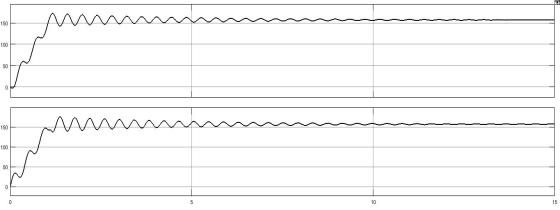
Рисунок 1.6 – Графики переходных процессов двухмассовой системы
Проведем сравнительный анализ графиков переходных процессов: в трехмассовой системе в отличии от двухмассовой колебания затухают быстрее. Это связано с тем, что во втором случае параметры движения приведены к наиболее податливому звену, и образованными двумя инерционными массами с моментами инерци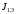и
и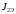 
. Т.е. уже не учитываются наиболее точно моменты упругой деформации и внутреннего вязкого трения между приведенными массами. Осуществим переход к относительным единицам в структурных схемах трехмассовой и двухмассовой систем
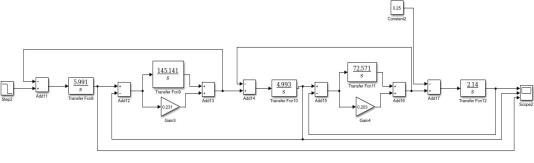
Рисунок 1.7 – Расчетная схема трехмассовой системы в относительных единицах
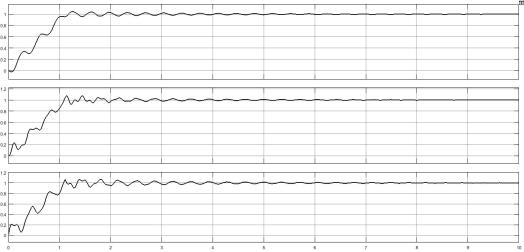
Рисунок 1.8 – Графики переходных процессов трехмассовой системы в а.е.
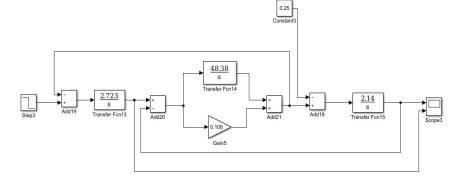
Рисунок 1.9 – Расчетная схема двухмассовой системы в абсолютных единицах
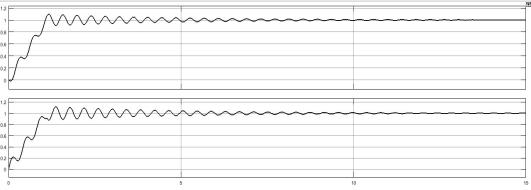
Рисунок 1.10 – Графики переходных процессов двухмассовой системы в а.е.
Видно, что графики переходных процессов в относительных единицах по форме и характеру ничем не отличаются от соответствующих графиков в абсолютных единицах. При этом модель приобрела более наглядный вид, что позволяет соотнести абсолютные величины сигналов с их базовыми значениями.
Для двухмассовой системы проведем моделирование с уменьшенным значением
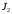в два раза: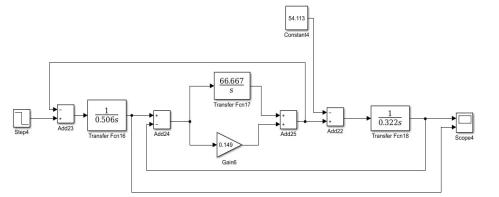
Рисунок 1.11 – Расчетная схема двухмассовой системы при уменьшении J2 в два раза
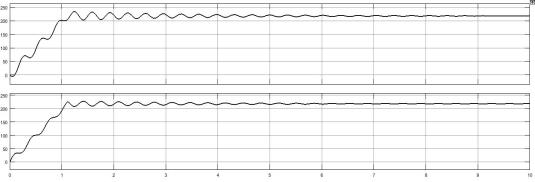
Рисунок 1.12 – График переходного процесса при уменьшении J2
Как мы видим, при уменьшении значения
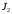произошло увеличение номинальной скорости при одном и том же входном воздействии. Также с уменьшением момента инерции 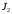график стал приобретать установившееся значение быстрее. Лабораторная работа № 2 Моделирование электродвигателя постоянного тока независимого возбуждения
Цель работы: исследование динамических свойств двигателя постоянного тока независимого возбуждения, выявление влияния параметров двигателя и нагрузки на динамические характеристики двигателя, получение навыков построения динамических характеристик при ненулевых начальных условиях.
Таблица 6.1 – Исходные данные
| № | Тип двигателя | Р2ном, кВт | Uя, В | Uв, В | nном, об/мин | Iя, А | Iв, А | Rя+Rдп, Ом | Rв, Ом | Lя, мГн | Lв, Гн | J, кг*м2 |
| 3 | 2ПН132М | 4 | 220 | 220 | 1500 | 21,65 | 1,37 | 1,08 | 160,8 | 11 | 18,4 | 0,038 |
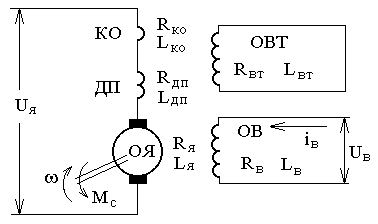
Рисунок 6.1 − Принципиальная электрическая схема двигателя постоянного тока независимого возбуждения
Физические процессы, протекающие в цепи якоря, описываются уравнением:
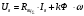, (6.1)Uя = 26,389 В;
Уравнение механического движения электродвигателя имеет вид:
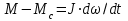, (6.2)55=0,415
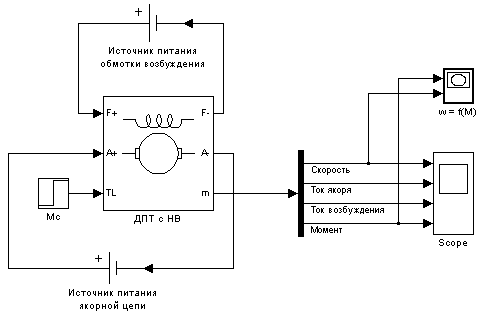
Рисунок 6.2 – Модель ДПТ с НВ для исследования переходных процессов
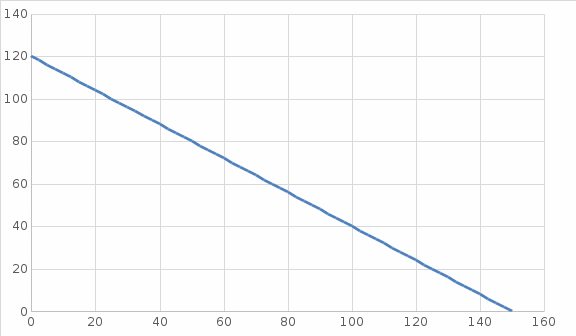
Рисунок 6.3 – Естественная механическая характеристика ДПВ НВ
Лабораторная работа № 3 Исследование режимов реостатного пуска электропривода постоянного тока
Цель работы: исследование механических характеристик двигателя постоянного тока независимого возбуждения при реостатном пуске; выявление влияния параметров пускового реостата и нагрузки на динамические характеристики двигателя.
При пуске двигателя в ход его ЭДС=0 и пусковой ток определяется только приложенным напряжением и сопротивлением якорной цепи:
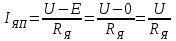(7.1)Izg = 880
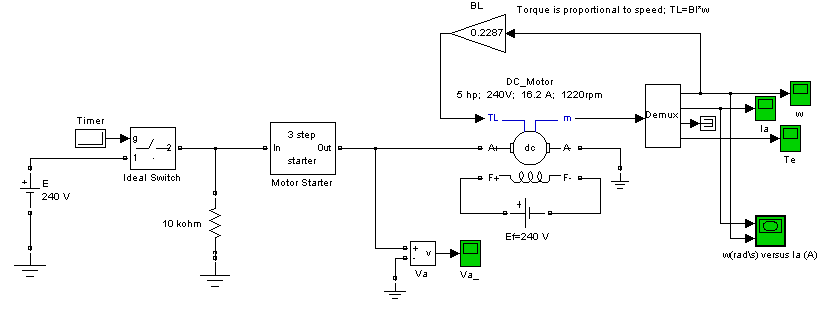
Рисунок 7.3 – Модель ДПТ с НВ для исследования переходных процессов при реостатном пуске
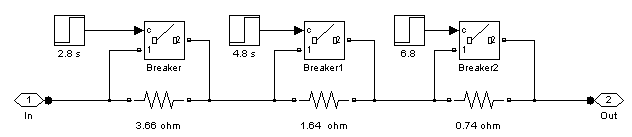
Рисунок 7.4 – Модель пускового реостата
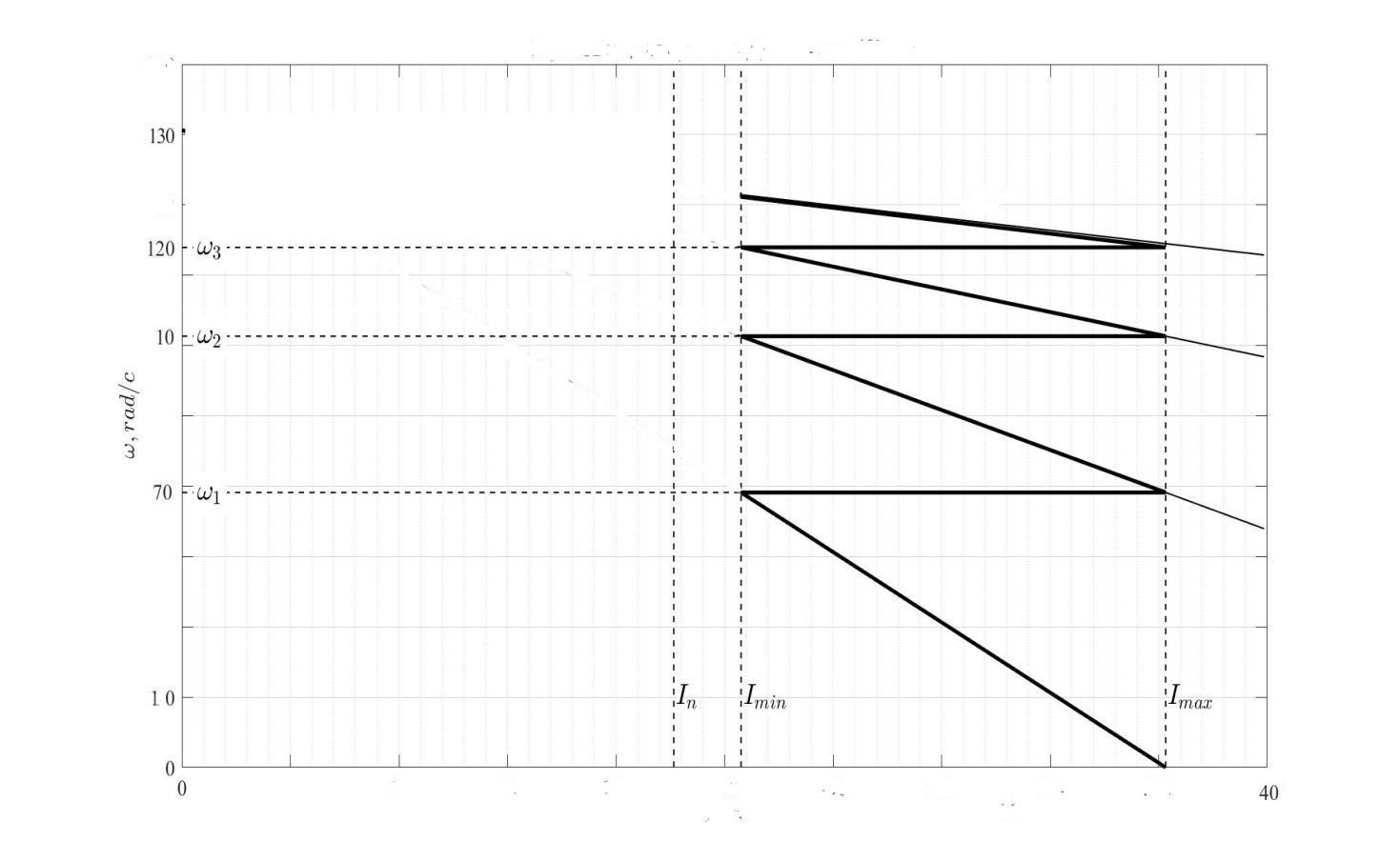Рисунок 7.5– Пусковая диаграмма ДПТ с НВ при реостатном пуске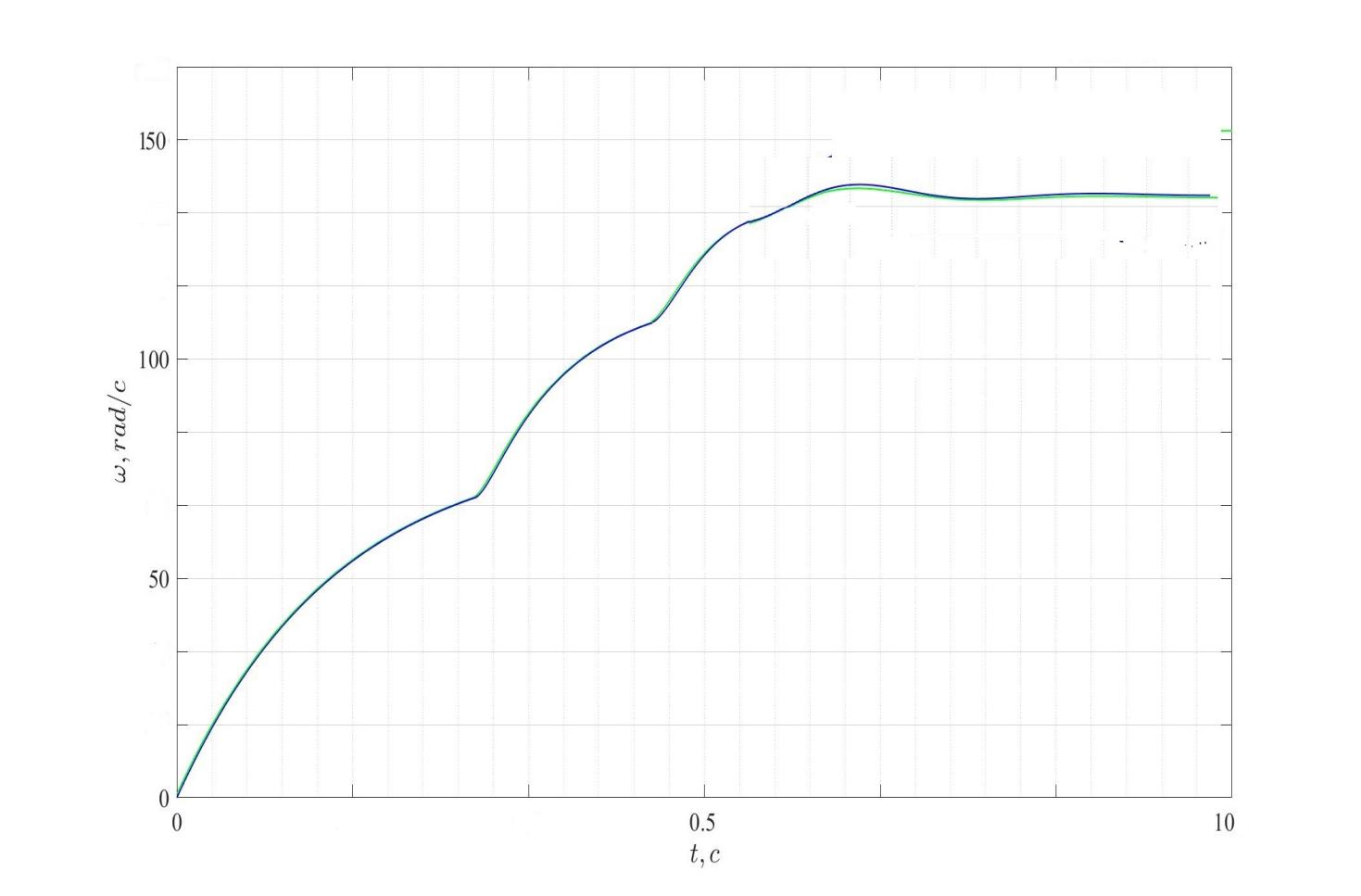
Рисунок 7.6–Зависимость скорости от времени пуска
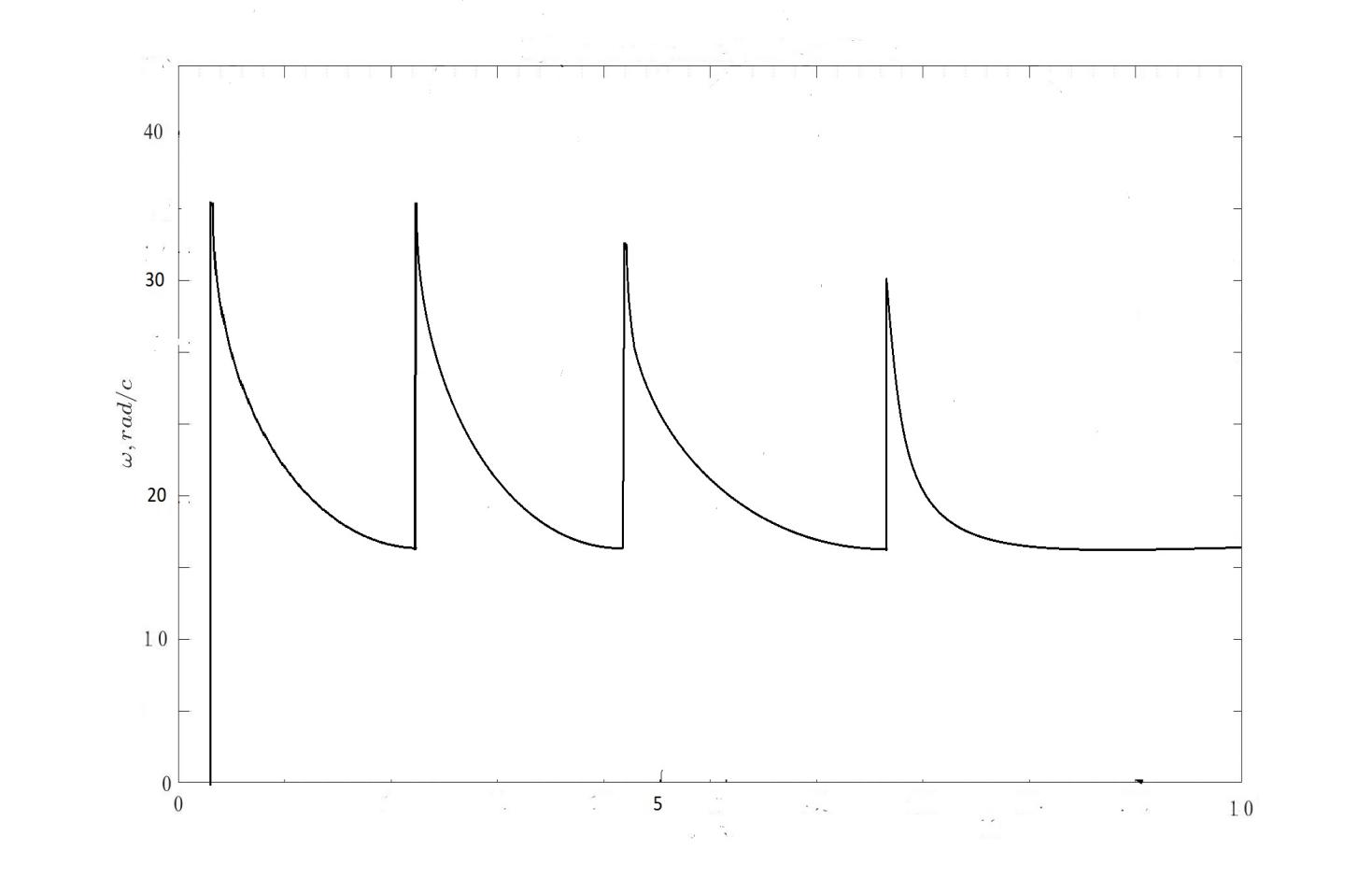
Рисунок 7.7–Зависимость тока от времени пуска
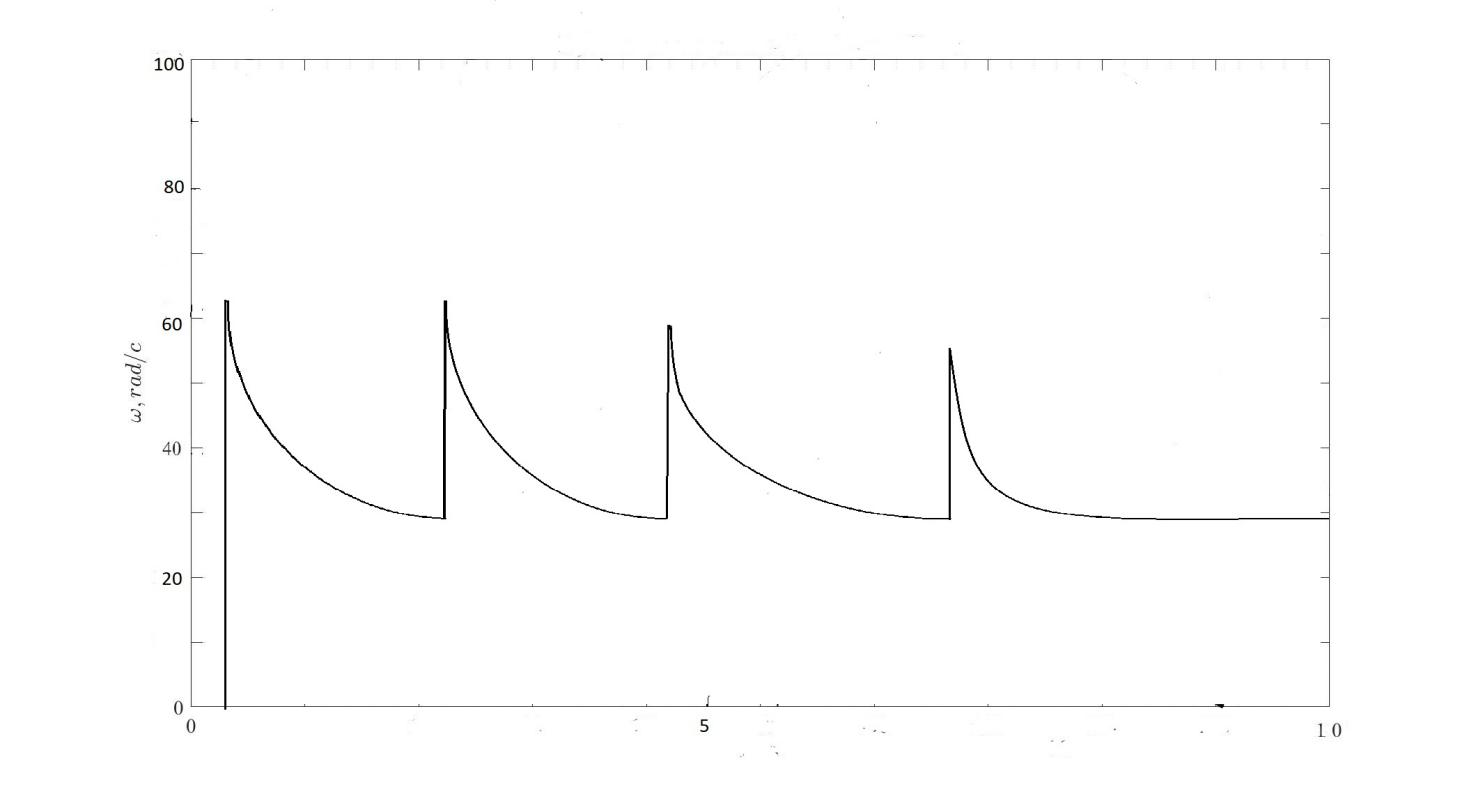
Рисунок 7.8‑ Зависимость скорости от тока при пуске двигателя
Лабораторная работа № 4 Исследование режима динамического торможения электропривода постоянного тока
Цель работы: исследование механических характеристик двигателя постоянного тока независимого возбуждения в режиме динамического торможения; выявление влияния параметров пускового реостата и нагрузки на динамические характеристики двигателя.
ЭД может работать в трех тормозных режимах – генераторном (рекуперативном), динамического торможения и в режиме противовключения.
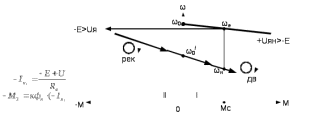
Рисунок 8.1 – Характеристики двигательного и рекуперативного режима торможения ЭД
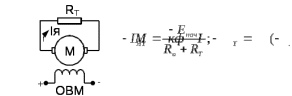
Рисунок 8.2 – Схема ЭД в динамическом режиме торможения
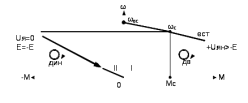
Рисунок 8.3 – Тормозная характеристика ЭД в динамическом режиме торможения
Расчеты сопротивления реостата динамического торможения.
Сопротивление реостата торможения рассчитывается по формуле
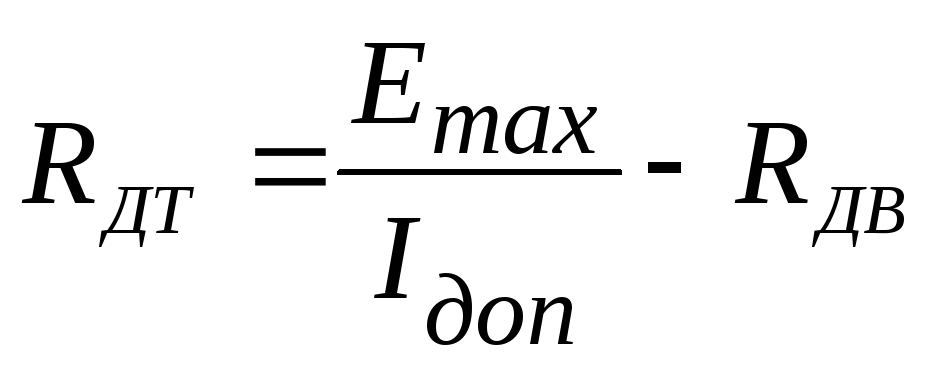
Rдт= 1,16 Ом
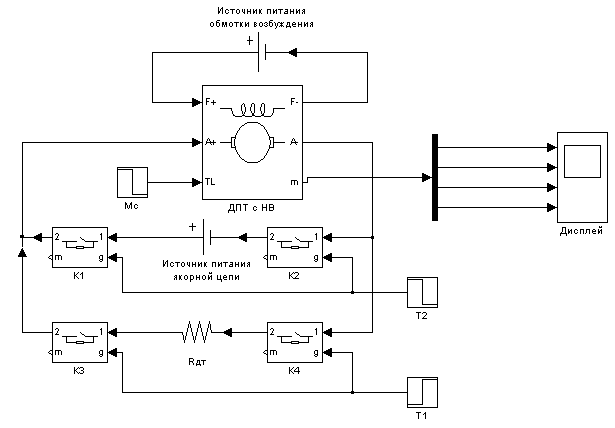
Рисунок 8.4 – Вариант модели ДПТ с НВ для исследования динамического торможения
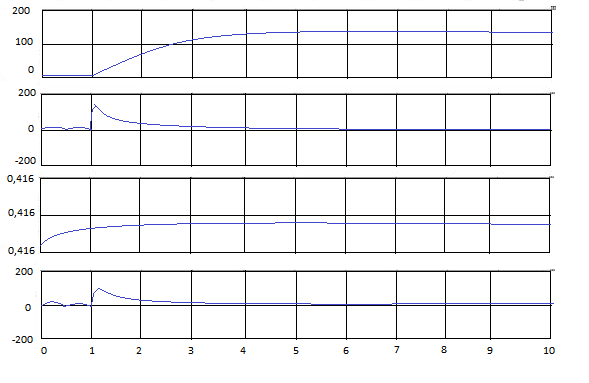
Рисунок 8.5 Временные характеристики скорости, тока и момента двигателя при динамическом торможении.