Файл: Первый ввопрос.docx

ПЕРВЫЙ ВВОПРОСДругие названия ФАЛ(функцией алгебры логики): логическая, булева или переключательная функция. В алгебре логики переменная может принимать одно из двух значений: True и False.2 способа описания:Словесный способ. Здесь все случаи, при которых функция принимает значения 0 или 1, опи- сываются словесно. Так, функцию «ИЛИ» со многими аргументами можно описать следующим обра- зом: функция принимает значение 1, если хотя бы один из аргументов принимает значение 1, иначе значение функции равна 0.Табличный способ. Булева функция задается в виде таблицы истинности. В левой части таблицы истинности записываются все возможные n-разрядные двоичные комбинации аргументов,а в правой – значения функции на этих наборах. Таблица ис- тинности содержит 2n строк.Числовой способ. Функция задается в виде последовательности десятичных эквивалентов тех наборов аргументов, на которых функция принимает значение 1. Например, двоичные наборы 010 и 101 имеют десятичные номера 2 и 5 соответственно.Аналитический способ. Предполагает описание ФАЛ в виде алгебраического выражения, получаемого путем применения к аргументам операций булевой алгебры.Ко ординатный способ. При этом способе задания таблица истинности заменяется коорди- натной картой состояний, известной под названием карты Карно. Такая карта содержит 2n клеток по числу возможных наборов из n переменных.Гр афический, или геометрический способ. Булева функция задается с помощью n-мерного куба. Множество наборов, на которых определена функция n переменных, представляется верши- нами n-мерного куба. Отметив точками те вершины куба, в которых функция принимает единичное (либо нулевое) значение, получаем геометрическое представление функции.2) Элементарные функции алгебры логики.

• 
  Алгебра логики (АЛ) является основным инструментом синтеза и анализа дискретных автоматов всех уровней. 
  
• 
  Алгебра логики называют также Булевой алгеброй.
  
• 
  АЛ базируется на трёх функциях, определяющих три основные логические операции.
  
• 
   Функция отрицания (НЕ). f1 =`X 
  
• 
   Функция логического умножения (конъюнкции). Функция логического умножения записывается в виде f2=X1·X2.  Конъюнкцию называют функцией И, элемент, реализующий эту функцию, элементом И.
  
• 
   Логическое сложение (дизъюнкция). Функция логического сложения записывается в виде f3=X1 + X2. функцию дизъюнкции часто называют функцией ИЛИ.
  

---

3) Правила алгебры логики.Правила эти определяются для двух возможных логических значений «1» (True) и «0» (False), а также трех базовых логических опе- раций: «НЕ», «И» и «ИЛИ. Базовые логические операции перечислены в порядке пониже- ния их приоритетности. Учет приоритетности операций позволяет сократить число скобок при записи логических выражений.1) ассоциативность2) коммутативность3) дистрибутивность4) Понятие логического базиса.Логическим базисом называется минимальный необходимый набор логических функций, с помощью которых может быть реализовано логическое выражение любой сложности.Функции И, ИЛИ, НЕ образуют основной логический базис.

• 
  "И-НЕ" (базис Шеффера)
  
• 
  "ИЛИ-НЕ" (базис Пирса или функция Вебба).
  

5) Аналитическое представление булевых функций.При аналити- ческой записи ФАЛ представляется либо в виде логической суммы элементарных логических произ- ведений (дизъюнкции элементарных конъюнкций), либо в виде логического произведения элемен- тарных логических сумм (конъюнкции элементарных дизъюнкций). Первая форма записи носит на- звание дизъюнктивной нормальной формы (ДНФ), вторая – конъюнктивной нормальной формы (КНФ).Элементарной конъюнкцией (элементарным логическим произведением) называют логическое произведение любого количества переменных (аргументов)Дизъюнктивная нормальная форма (ДНФ) – это логическая сумма элементарных логических произведенийМинтерм (единичный набор функции) – это логическое произведение всех переменных, взятых с отрицанием или без.Совершенной дизъюнктивной нормальной формой (СДНФ) называется ДНФ, состоящая из всех минтермов булевой функции. Для получения СДНФ на основе таблицы истинности необходимо:1)каждый из входных наборов, на которых булева функция принимает значение «1»,представить в виде элементарного произведения (конъюнкции).2)полученные элементарные логические произведения объединить знаками логического сложения (дизъюнкции).6) Минимизация логических функций и ее цели.Проблема минимизации логических выражений проистекает из практических задач создания логических схем. В качестве исходной аналитической формы обычно рассматривают совершенные ДНФ и КНФ

---

, которые во многих случаях оказываются излишне сложными, из-за чего их техническая либо программная реализация получается избыточной. Для упрощения СДНФ и СКНФ используются различные методы минимизации – преобразования логической функции с целью упрощения ее ана- литической записи.

7) Минимизация логических функций методом Квайна

1. Нахождение простых импликант




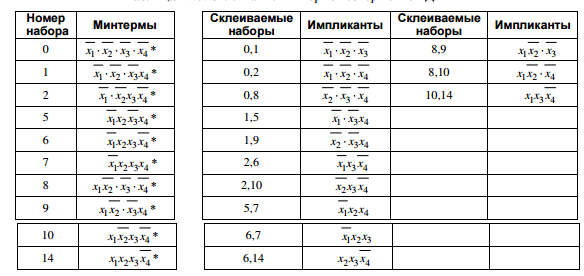
2. Составление импликантной матрицы и расстановка меток избыточности




3.  Нахождение существенных импликант и исключение связанных с ними строк и столбцов

4. Определение и запись минимальной нормальной формы

8) Минимизация по методу Квайна – Мак-Класски

Метод Квайна – Мак-Класски отличается от метода Квайна только в той части, которая связана со способом нахождения простых импликант. Описанная модификация заменяет лишь первый шаг метода Квайна, при этом все последую- щие шаги производятся аналогично методу Квайна.

9) Минимизация логических функций методом Петрика.

Метод Петрика (Petrick) также имеет целью упрощение метода Квайна, но в части нахожде- ния всех тупиковых форм по импликантной матрице.

10 ) Минимизация логических функций методом карт Карно.

11) Минимизация частично определенных функций.

Наиболее удобно это производить с помощью карт Карно.



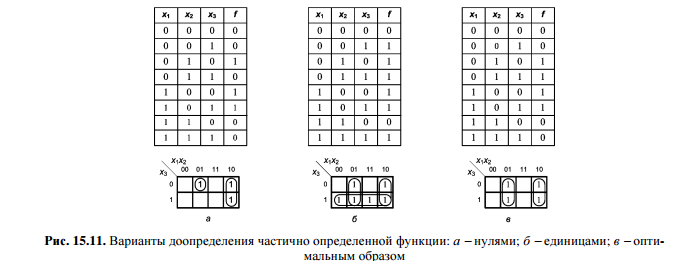
Принимаю * за 1 или 0.

12) Сигналы в цифровой схемотехнике.

Цифровой сигнал – это сигнал, который может принимать два значения, рассматриваемые как логическая «1» и логический «0». Устройства, работающие только с цифровыми сигналами, называ- ются цифровыми устройствами.

положительный сигнал (сигнал положительной полярности) – сигнал, активный уровень которого – логическая «1» («0» соответствует отсутствию сигнала);

отрицательный сигнал (сигнал отрицательной полярности) – сигнал, активный уровень которого – логический «0» («1» соответствует отсутствию сигнала);

---

13) Логические элементы и их графическое обозначение.Логический элемент «НЕ» - противоположное значение сигнала.Логический элемент «И» - всегда 1Ло гический элемент «ИЛИ» -всегда 0Ло гический элемент «И-НЕ» -0Эл емент «ИЛИ-НЕ» -114) Положительная и отрицательная логика.На 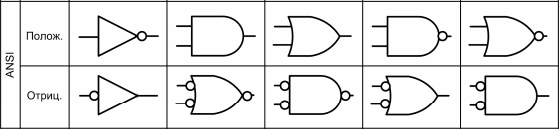пряжения на входах и выходах логических элементов могут принимать два уровня: высо- кий (H – high) и низкий (L –low). Если высокий уровень соответствует логической «1», а низкий уро- вень – логическому «0», то принято считать, что логический элемент работает с положительной логи- кой. Если высокий уровень соответствует логическому «0», а низкий уровень – логической «1», то элемент работает с отрицательной логикой15) Мультиплексоры и демультиплексоры.Mультипле́ксор — устройство, имеющее несколько сигнальных входов, один или более управляющих входов и один выход. Мультиплексор позволяет передавать сигнал с одного из входов на выход; при этом выбор желаемого входа осуществляется подачей соответствующей комбинации управляющих сигналов.Мультиплексоры могут использоваться для преобразования параллельного двоичного кода в последовательный. Мультиплексоры могут использоваться в, триггерных устройствах,Де мультиплексор  Они обеспечивают подключение единственного входа к одному из m выходов. При необходимости увеличить число выходных каналов можно построить логическую струк- туру демультиплексорного дерева. мультиплексор можно построить на основе точно таких же схем логического "И", как и при построении мультиплексора. 16) Шифраторы и дешифраторы.

• 
  Шифратором (кодером) называется комбинационное логическое устройство для преобразо- вания n-разрядного унитарного кода в m-разрядный параллельный код.
  
• 
  Максимальное число входов шифраторов не превышает количества возможных комбинаций выходных сигналов (n <= 2 m ).
  
• 
  В результате шифрации происходит «сжатие» информации.
  
• 
  Одно из основных применений шифратора – ввод данных с кла­виатуры, при котором нажатие клавиши с десятичной цифрой должно приводить к передаче в устройство двоичного кода данной цифры
  

---

• 
  Дешифратором (декодером) называют устройство с несколькими входами и выходами, у ко- торого определённым комбинациям входных сигналов соответствует активное состояние одного из выходо
  
• 
  Дешифратор называется полным, если число выходов равно максимально возможной разрядности выходного слова (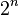 ). Дешифратор называется неполным, если часть входных разрядов не используется (то есть число выходов меньше  ).
  
• 
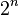  они могут преобразовывать двоичный код в разные системы счисления
  

17) Преобразователи кодов.

• 
  Преобразователи кодов (конвертеры) обеспечивают перевод информации из одной формы в другую
  
• 
  Шифраторы, дешифраторы- преобразователи кодов.
  

18) Схемы контроля четности.

• 
  Простой и эффективный способ обнаружения ошибок при записи, чтении и передаче информации основан на допущении, что в каждый момент времени ошибка может возникнуть только в одном разряде, и проявляется она в лишней единице или в потере единицы. В обоих случаях число единиц в коде изменяется на одну.Если передаваемая кодовая комбинация содержит чётное число единиц по всем разрядам, а на конце линии передачи это число окажется нечётным, значит, появилась ошибка
  
• 
  На передающей стороне формируется контрольный, или паритетный бит. бит передаётся вместе с информацией.
  
• 
  Паритет может быть чётным или нечётным
  
• 
  В случае нечётного паритета контрольный бит формируется таким образом, чтобы сумма всех единиц в передаваемом коде, включая контрольный бит, была чётной. На практике нечётный паритет используется чаще, так как позволяет фиксировать полное пропадание информации
  
• 
  При проверке как чётности, так и нечётности в случае отсутствия ошибки на выходе схемы контроля обычно формируется логическая «1», а при ошибочном – логический «0».
  

19) Цифровые компараторы.

• 
  логическое устройство с двумя входами, на которые подаются два разных двоичных слова равной в битах длины и тремя двоичными выходами, на которые выдаётся сравнения входных слов, — первое слово больше второго, меньше или слова равны.
  
• 
  Компараторы широко используются в вычислительной технике, измерительной технике, радио- и проводной связи, бытовых приборах. Например, цифровые часы с будильником содержат цифровой компаратор, при совпадении текущего времени с заданным подается звуковой сигнал.
  

---