Файл: Формула Тейлора Разложить многочлен по степеням двучлена двумя способами (с помощью формулы Тейлора и без нее). 2.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 21
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Формула Тейлора
1. Разложить многочлен
2. Разложить функцию
3. Разложить функцию
4. Записать пять первых членов формулы Маклорена для функции
Используя известные разложения для элементарных функций, записать формулы Маклорена для следующих функций.
5.
9.
14.
17.
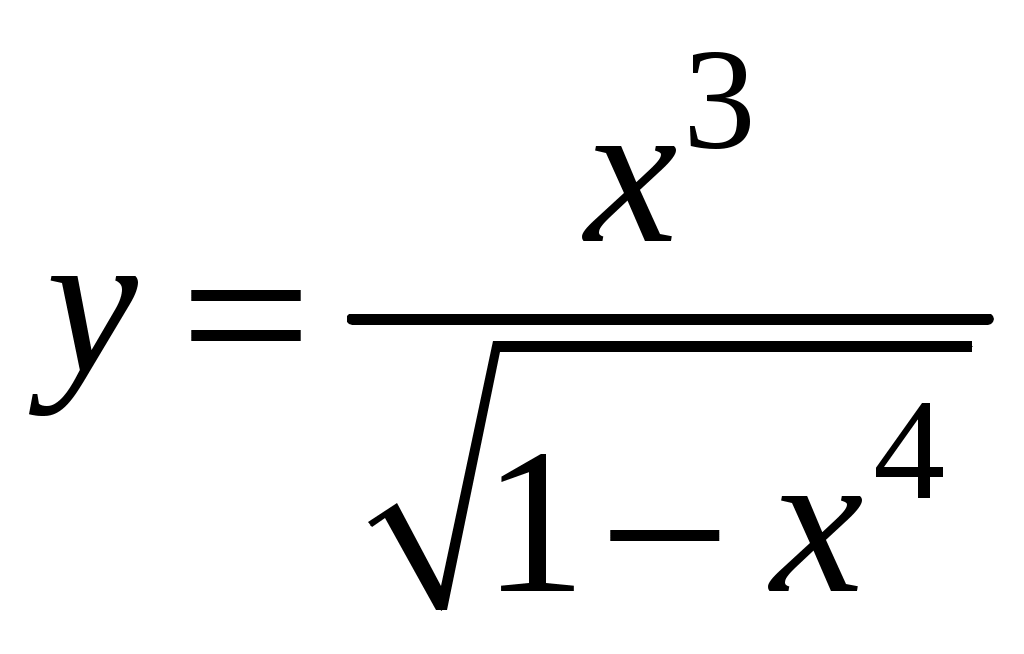
. 19.
Д.З. 1. Разложить многочлен
2. Разложить функцию
3. Записать пять первых членов формулы Маклорена для функции
Используя известные разложения для элементарных функций, записать формулы Маклорена для следующих функций.
5.
9.
13.
16.
 . 18.
. 18. Задания для самостоятельной работы 1
Разложить в ряд Фурье следующие периодические функции с периодом
1.
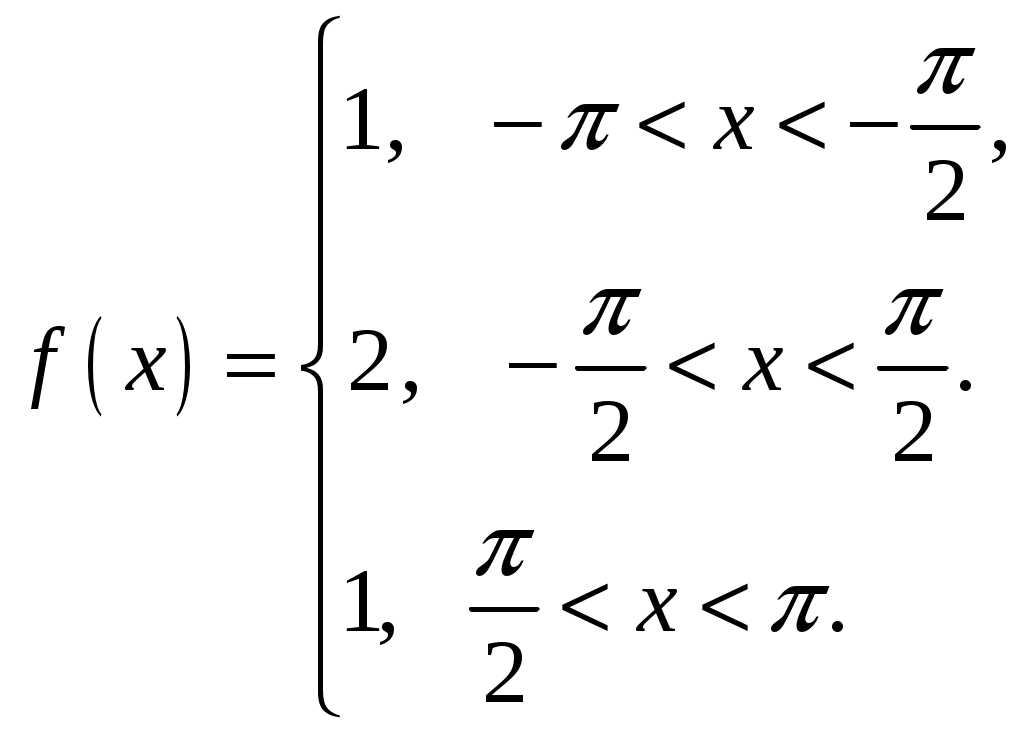
2.
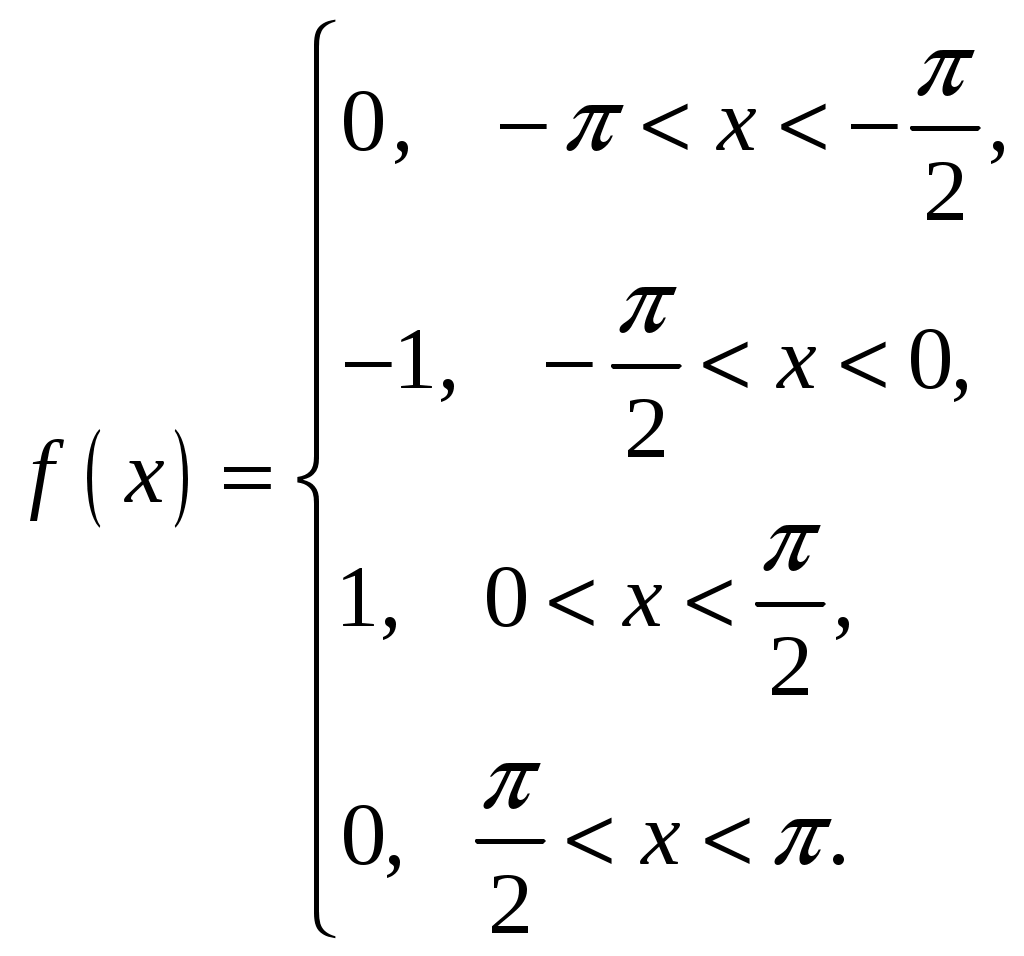 3.
3. 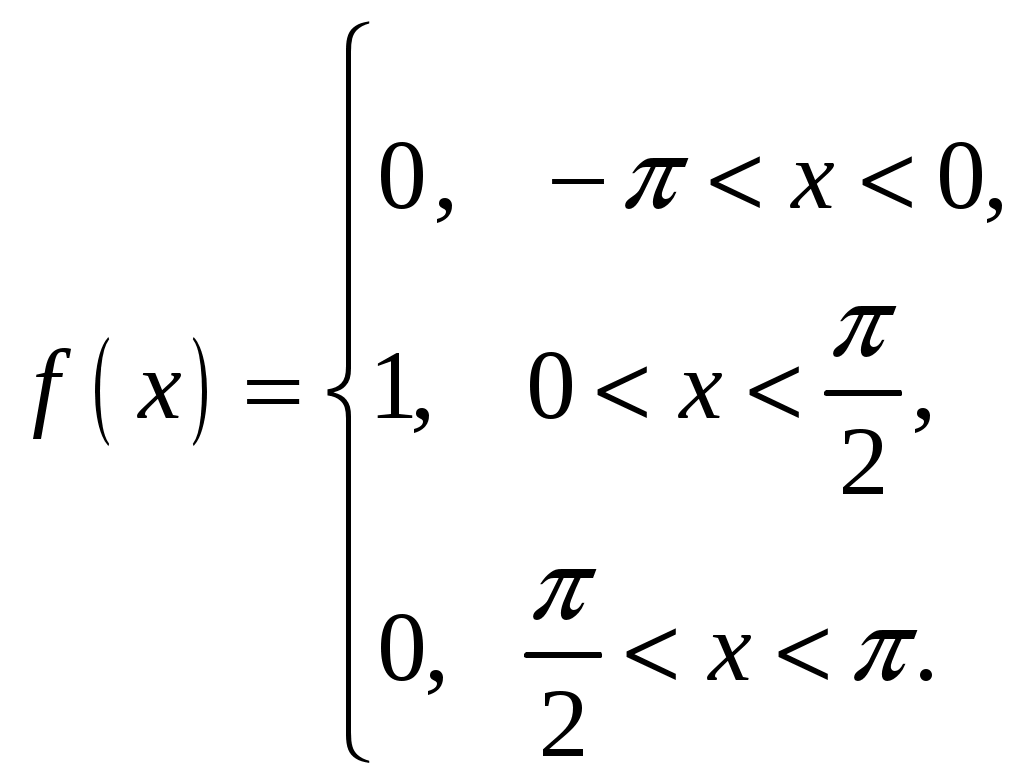
4.
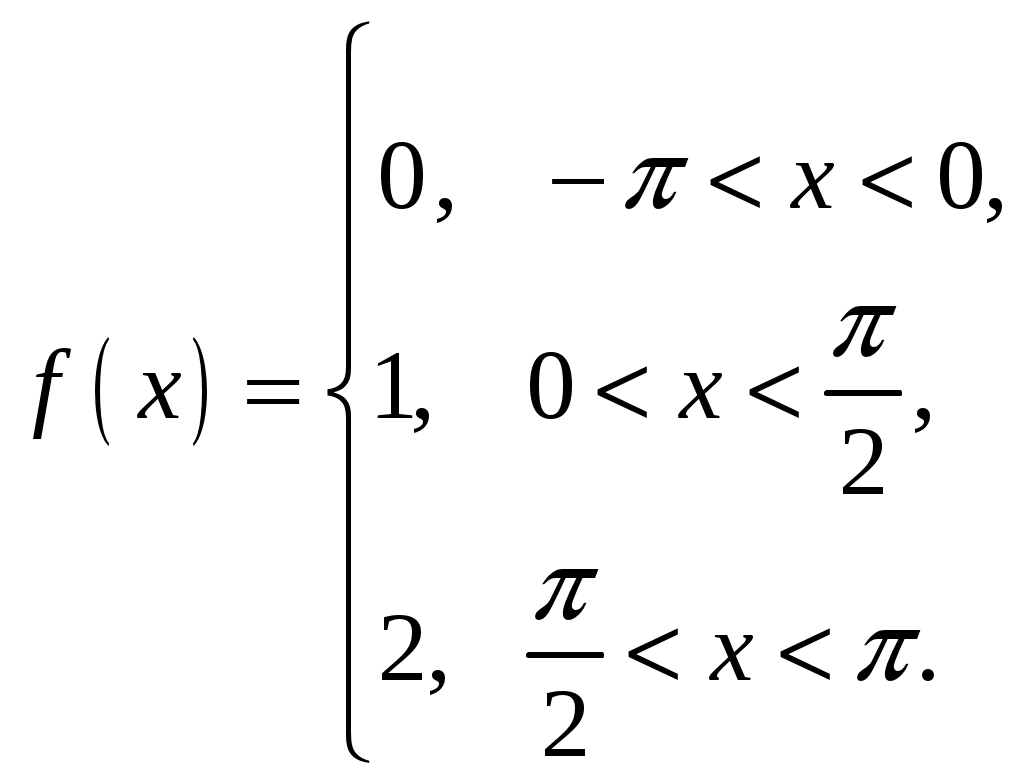 Ответы: 1.
Ответы: 1. 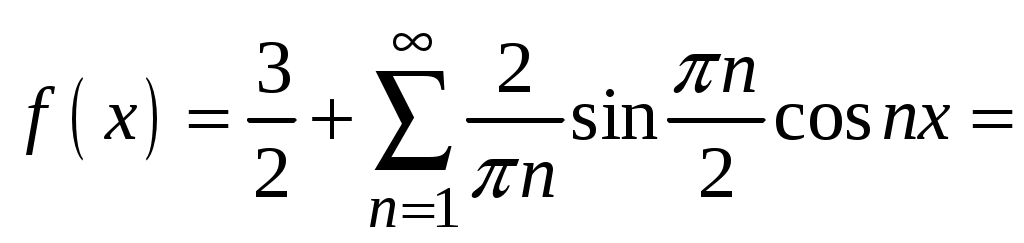
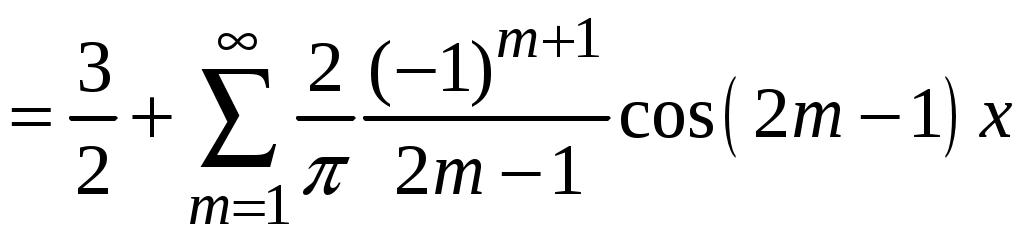 . 2.
. 2. 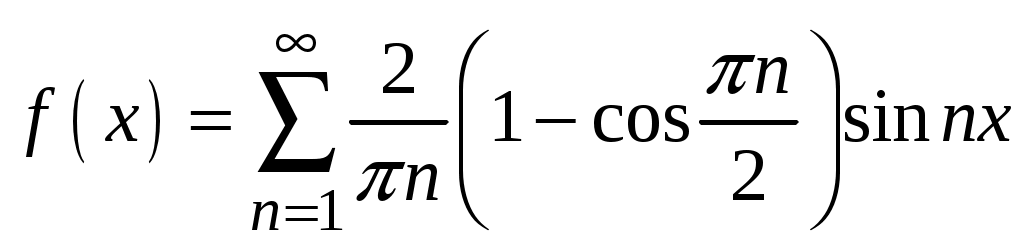 .
.3.
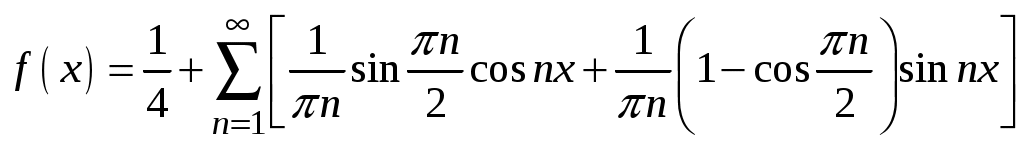 . (см. на об)
. (см. на об)Задания для самостоятельной работы 2
1. Разложить функцию
2. Разложить функцию
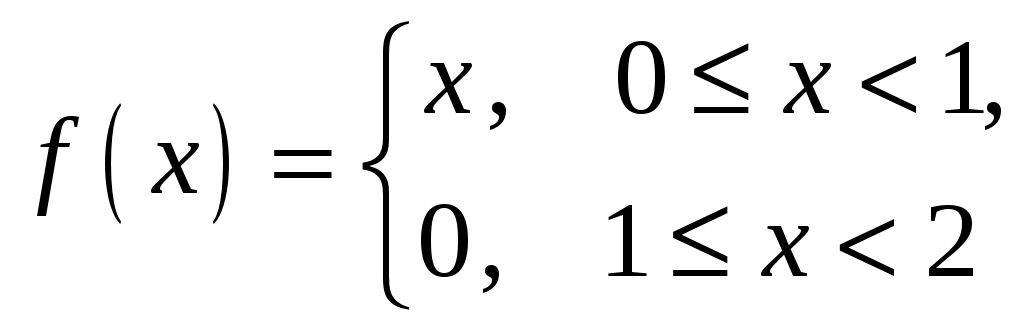 в ряд Фурье по синусам.
в ряд Фурье по синусам.3. Разложить функцию
4. Разложить функцию
Ответы: 1.
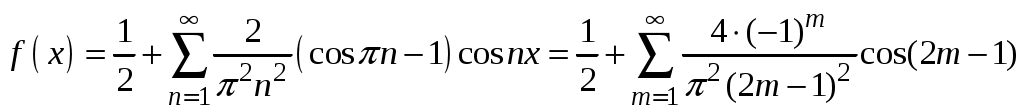 .
.2.
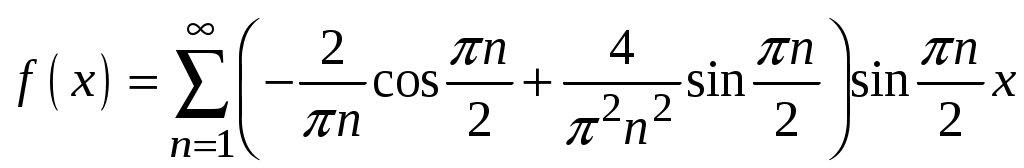 .
.3.
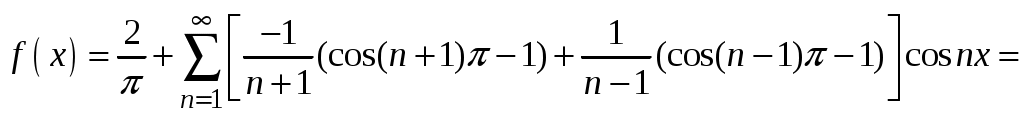
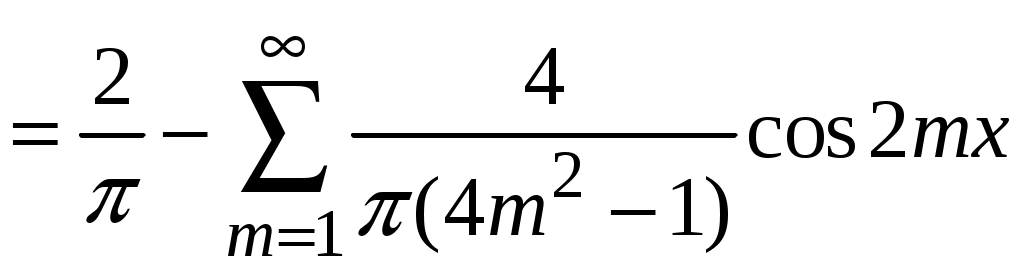 . 4.
. 4. 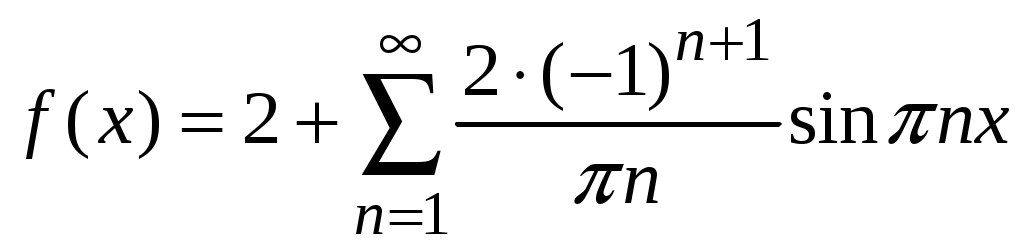 .
.4.
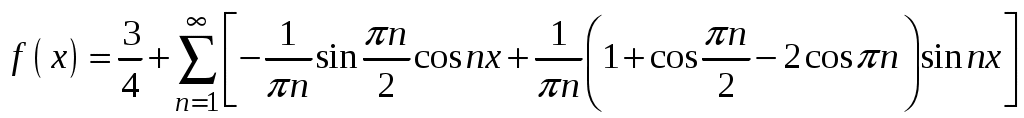 .
.Числовые ряды (повторение)
Исследовать ряды на сходимость
1.
. 3.
4.
7.
10.
14.
17.
20.
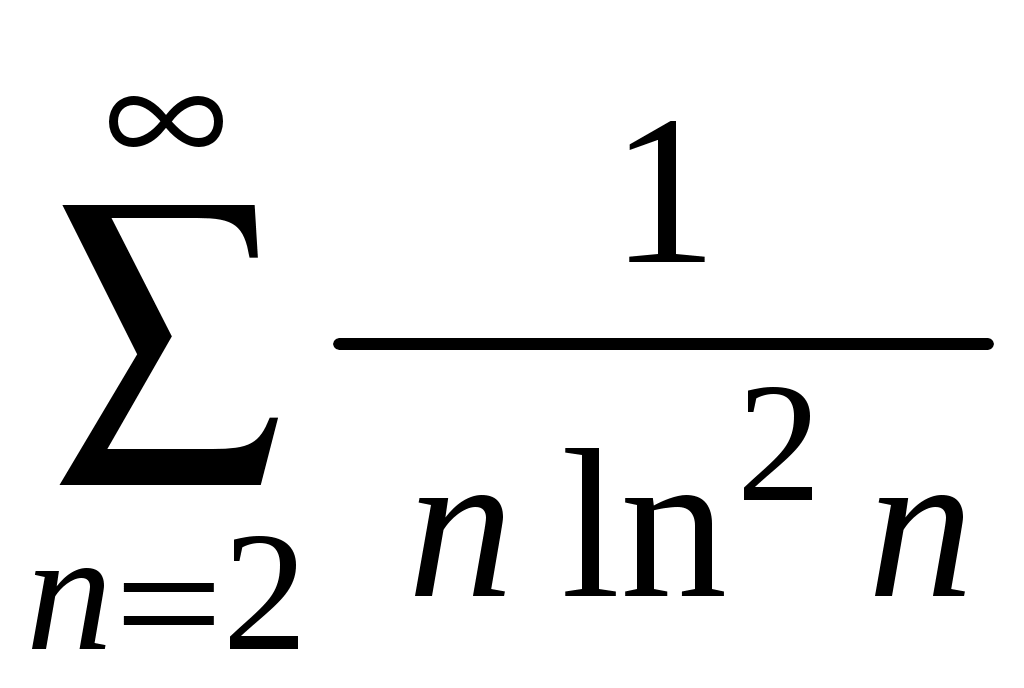 . 23.
. 23. 24.
27.
. 30.
31.
Ряды
Д.З. Демидович, №№ 2417, 2418, 2420, 2421, 2423, 2425.
Д.З. Демидович, №№ 2427, 2429, 2438, 2439, 2441, 2455, 2457, 2460, 2464.
Д.З. Демидович, №№ 2470, 2473, 2474, 2475, 2477, 2481, 2482.
Д.З. Демидович. №№ 2527, 2528, 2532, 2535, 2538, 2546.
Д.З. Демидович, №№ 2590, 2594, 2595, 2597, 2600, 2614, 2625.
Д.З. Демидович, №№ 2644, 2645, 2648, 2653, 2654.
Кратные интегралы
Д.З. Демидович, №№ 2115, 2123, 2135а, 2137, 2146, 2150, 2152а.
Д.З. Демидович, №№ 2165
Д.З. Демидович, №№ 2240, 2243, 2244, 2247, 2248, 2265.
Д.З. Демидович, №№ 2241, 2242, 2243, 2249, 2253, 2555, 2557.
Д.З. Демидович, №№ 2213, 2227, 2231, 2262, 2269.
Свести двойной интеграл
Решение.
I способ. Область G изображена на Рис. 1, а. При каждом значении x из отрезка [0, 1] переменная yизменяется от x2 до 2x, т. е. область G можно представить в виде G = {(x, y): 0 ≤ x ≤ 1, x2 ≤ y ≤ 2x}. По формуле
II способ. Чтобы воспользоваться формулой