Файл: Тема Кинематика точки.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 26.10.2023

Просмотров: 111

Скачиваний: 22

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Практическое задание 4


Тема 2.1. Кинематика точки

Задание

Точка М движется в плоскости ХОY. Уравнения движения точки:

(см); (см). Найти уравнение траектории точки; построить эту траекторию; для момента времени, равного С (с), определить и показать на рисунке: положение точки, ее скорость, касательное, нормальное и полное ускорения; а также радиус кривизны траектории.
Рекомендации по выполнению задания 4

  1. Выделите точку, совершающую движение.

  2. Проведите анализ движения точки.

  3. Найдите уравнение траектории точки.

  4. Изобразите точку на рисунке в заданный момент времени.

  5. Определите скорость точки.

  6. Постройте вектор скорости точки по касательной к траектории.

  7. Определите ускорение точки.

  8. Постройте вектор ускорения точки.

  9. Найдите радиус кривизны траектории.


Бланк выполнения задания 4


1. Записываются данные задания.

С=8; П=7; Г=8;

;

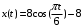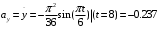
2. Представляется рисунок, на котором показана траектория движения точки.

Имеем закон движения точки в координатной форме. Чтобы получить уравнение траектории, исключим из заданных уравнений движения время t

;

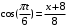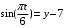
Возводим в квадрат и складываем:

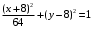- ‘эллипс

;

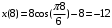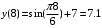
3. Находится скорость точки.





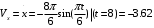
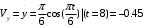
4. Находятся все ускорения точки.

;


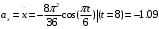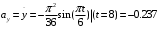
Модуль ускорения равен 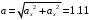; модуль касательного ускорения равен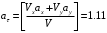

Модуль нормального ускорения 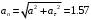, где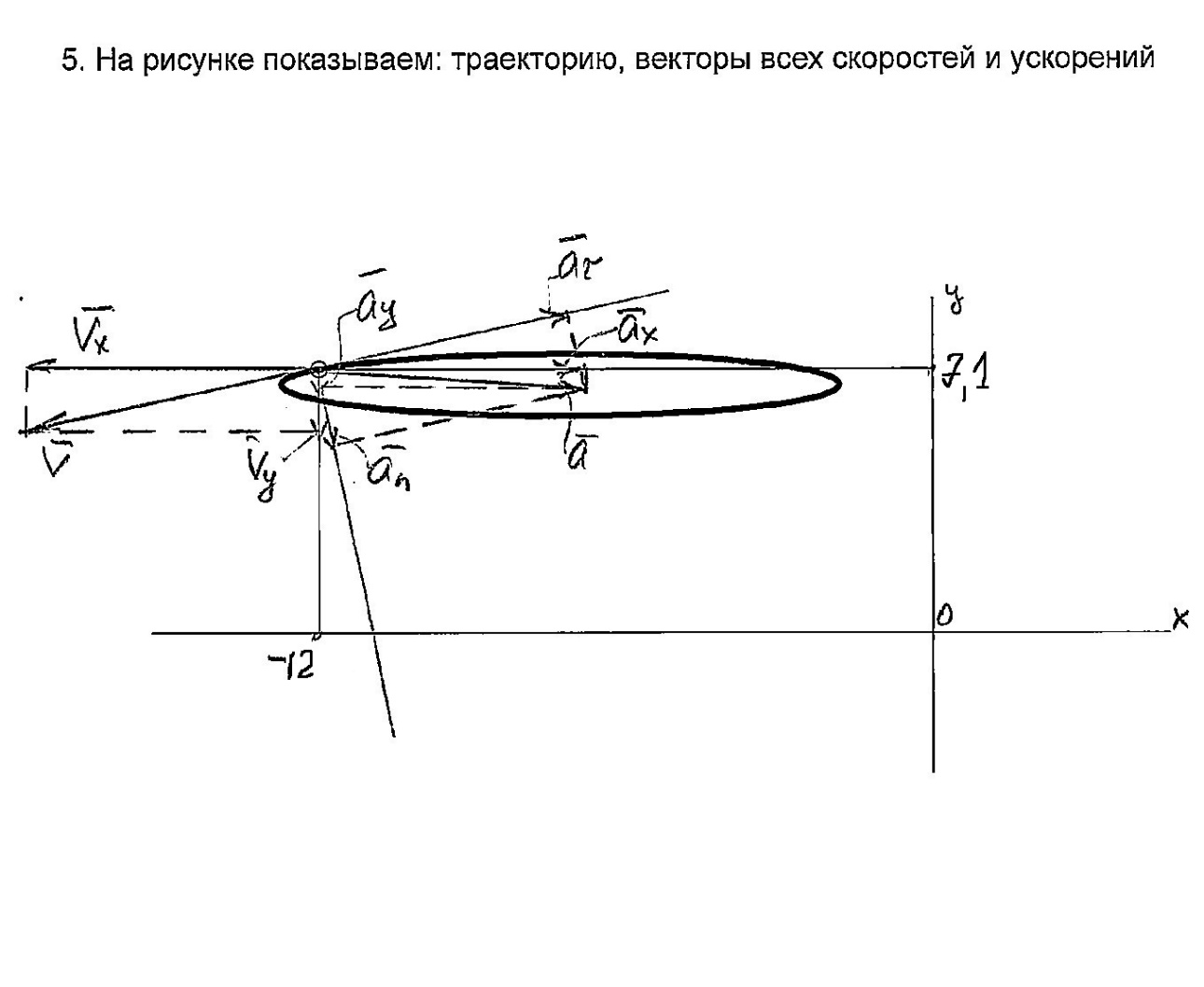


6. Находится радиус кривизны траектории.

радиус кривизны равен



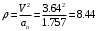
7. Записывается ответ.

Ответ при t=8 с,
х=-12 см; н=7,1 см; V=3,64 см/с; а=1,11 см/с2 ; а 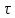=1,11 см/с2 ; аn=1,57;
ρ=8,44 см

Смотрите также файлы