МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕУЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»(СПбГУТ)ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯДисциплина: Теория информации, знания, данныеЛАБОРАТОРНАЯ РАБОТА 7«Решение задачи регрессии с помощью нейронной сети»Вариант 1Фамилия: ГригорьевИмя: МаксимОтчество: ДмитриевичГруппа №: ИБ-16с № Зач: 2110871Проверил:______________Санкт-Петербург2023Цель работы – исследование принципов разработки нейронной сети на примере задачи регрессии.Задание на лабораторную работу 1. Исследовать нейронную сеть при заданных начальных параметрах.

Вариант	Метод оптимизации	Число нейронов в скрытом слое n_hidden_neurons	Шаг градиентного спуска lr
1	ADAM	20	0.001

Найти минимальное значение n_hidden_neurons, при котором сеть дает удовлетворительные результаты. 2. Найти наилучшее значение шага градиентного спуска lr в интервале +-100% от номинального значения. 3. Изменить нейронную сеть для предсказания функции y = 2x*sin(2 −x )4. Для этой задачи (п. 3) получите метрику не хуже 0.03, варьируя: архитектуру сети, loss-функцию, lr оптимизатора или количество эпох в обучении. 5. Метрика вычисляется с помощью выражения (pred-target).abs().mean() и выводится оператором print(metric(sine_net.forward(x_validation), y_validation).item()).Описание методики исследования Для решения поставленной задачи используем нейронную сеть c одним полносвязным скрытым слоем. Обучать нейронную сеть будем на размеченной обучающей выборке. Прежде чем рассматривать процесс обучения нейронной сети, мы рассмотрим понятие размеченной обучающей выборки. Размеченная обучающая выборка

---

состоит из какого-то количества объектов, для которых мы знаем две вещи: во-первых, это некоторые признаки x1 … xN. Для каждого объекта мы знаем некоторый набор признаков. Кроме того, мы знаем некоторую метку объекта у1 … уN. Мы можем на этом обучить некоторую нейронную сеть. Но, прежде чем обучать нейронную сеть, мы разделим эту выборку на три части: тренировочный датасет, валидационный датасет и тестовый датасет. Тренировочный датасет – это то, что мы непосредственно используем для обучения нашей модели. Валидационный датасет нужен для того, чтобы подстраивать параметры обучения нашей модели (гиперпараметры). На самом деле его никогда не используют в процессе обучения, но мы подгоняем некоторые параметры, чтобы на этом датасете результаты были лучше. Тестовый датасет – это датасет, на котором мы будем проверять окончательный результат. Если у нас получится хороший результат на тестовом датасете, это означает, что наша модель обобщила информацию, которая ей была предоставлена.

Для обучения нейронной сети будет использован метод ADAM – adaptive moment estimation – оптимизационный алгоритм. Он сочетает в себе идею накопления движения и идею более слабого обновления весов для типичных признаков.
Ход работы

1. Ниже представлен линстинг кода, выполняющего исследование нейронной сети при заданных начальных параметрах и результат обучения нейронной сети
##

import torch

import matplotlib.pyplot as plt

##

##

import matplotlib

matplotlib.rcParams['figure.figsize'] = (13.0, 5.0)

##

##

x_train = torch.rand(100)

x_train = x_train * 20.0 - 10.0

y_train = torch.sin(x_train)

plt.plot(x_train.numpy(), y_train.numpy(), 'o')

plt.title('$y = sin(x)$');

##

##

noise = torch.randn(y_train.shape) / 5.

plt.plot(x_train.numpy(), noise.numpy(), 'o')

plt.axis([-10, 10, -1, 1])

plt.title('Gaussian noise');

y_train = y_train + noise

plt.plot(x_train.numpy(), y_train.numpy(), 'o')

plt.title('noisy sin(x)')

plt.xlabel('x_train')

---

plt.ylabel('y_train');

##

##

x_train.unsqueeze_(1)

y_train.unsqueeze_(1);

##

##

x_validation = torch.linspace(-10, 10, 100)

y_validation = torch.sin(x_validation.data)

plt.plot(x_validation.numpy(), y_validation.numpy(), 'o')

plt.title('sin(x)')

plt.xlabel('x_validation')

plt.ylabel('y_validation');

x_validation.unsqueeze_(1)

y_validation.unsqueeze_(1);

##

##

class SineNet(torch.nn.Module):

 def __init__(self, n_hidden_neurons):

  super(SineNet, self).__init__()

  self.fc1 = torch.nn.Linear(1, n_hidden_neurons)

  self.act1 = torch.nn.Sigmoid()

  self.fc2 = torch.nn.Linear(n_hidden_neurons, 1)

 def forward(self, x):

  x = self.fc1(x)

  x = self.act1(x)

  x = self.fc2(x)

  return x

  

sine_net = SineNet(20)

##

##

def predict(net, x, y):

 y_pred = net.forward(x)

 plt.plot(x.numpy(), y.numpy(), 'o', label='Groud truth')

 plt.plot(x.numpy(), y_pred.data.numpy(), 'o', c='r', label='Prediction');

 plt.legend(loc='upper left')

 plt.xlabel('$x$')

 plt.ylabel('$y$')

predict(sine_net, x_validation, y_validation)

##

##

optimizer = torch.optim.Adam(sine_net.parameters(), lr=0.001)

##

#test_accuracy_history = []

#test_loss_history = []

##

def loss(pred, target):

 squares = (pred - target) ** 2

 return squares.mean()

##

##

for epoch_index in range(2000):

 optimizer.zero_grad()

 y_pred = sine_net.forward(x_train)

 loss_val = loss(y_pred, y_train)

 loss_val.backward()

 optimizer.step()

# test_preds = sine_net.forward(x_validation)

# test_loss_history.append(loss(test_preds, y_validation))

predict(sine_net, x_validation, y_validation)

##

##

#plt.plot(test_loss_history);

## 

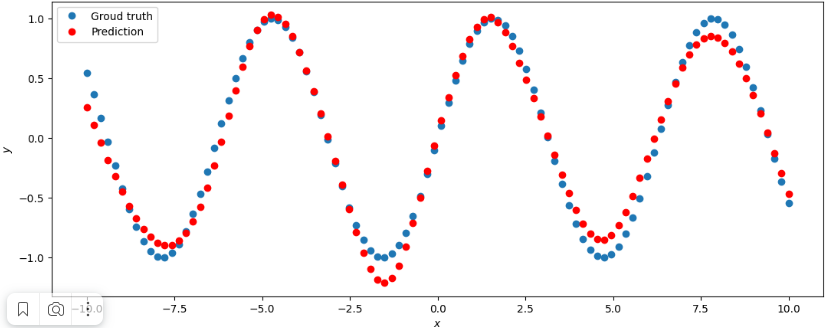
Рисунок 1 – Результат обучения нейронной сети при заданных значениях
Минимальное значение n_hidden_neurons, при котором сеть дает удовлетворительные результаты = 5.
2. Для нахождения наилучшего значения шага градиентного спуска lr в интервале +-100% от номинального значения код из задания 1 был модифицирован следующим образом:

1. После создания класса SineNet добавлена переменная index, весь следующий код обернут в цикл while:
index = 0
while index < 0.02:

#код обучения нейронной сети

index+=0.001
2. Метод вывода результата модифицирован следующим образом:

     def predict(net, x, y):

        y_pred = net.forward(x)

        if index == 0:

          plt.plot(x.numpy(), y.numpy(), 'o', label='Groud truth')

        

        label = 'Prediction ' + str(index)

        plt.plot(x.numpy(), y_pred.data.numpy(), 'o', label=label);

        

        plt.legend(loc='upper left')

        plt.xlabel('$x$')

        plt.ylabel('$y$')
Результат выполнения модифицированного кода представлен на рисунке 2.

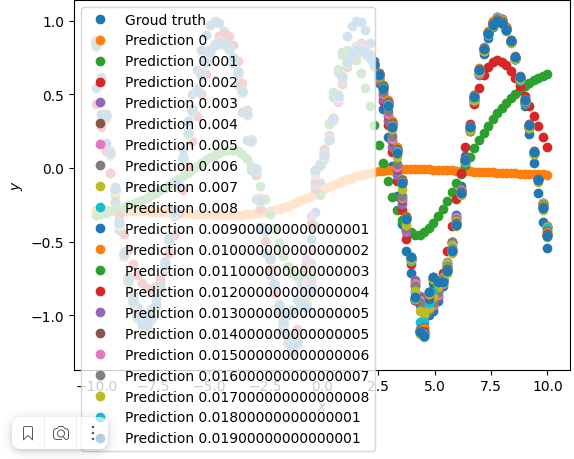
Рисунок 2 – Результат выполнения модифицированного кода

Результат был проанализирован, после чего диапазон цикла был уменьшен до 0.003 - 0.012. На рисунке 3 представлен результат выполнения кода в данном диапазоне.

---

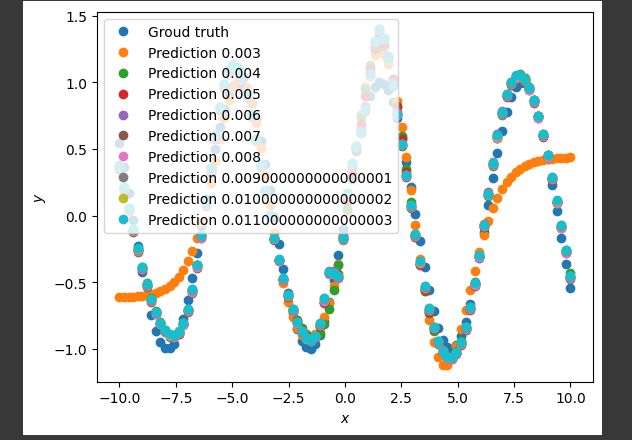
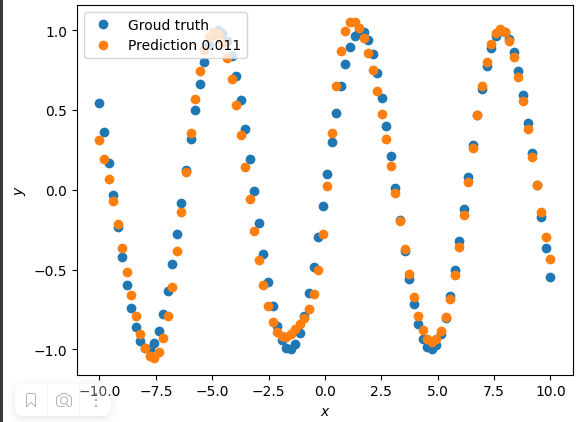
Рисунок 2 – Результат выполнения модифицированного кода в диапазоне 0.003 - 0.012Затем, методом подбора уменьшались границы диапазона. Таким образом было установлено, что наилучшим значением градиентного спуска lr в интервале +-100% от номинального значения будет значение lr = 0.11. На рисунке 3 представлен результат выполнения кода при lr = 0.011.Рисунок 3 – Результат выполнения кода при lr = 0.0113. Для для предсказания функции y = 2 x * sin(2 −x ) нейронная сеть была изменена следующим образом:def target_function(x):return 2**x * torch.sin(2**-x)# ------Dataset preparation start--------x_train = torch.linspace(-10, 5, 100)y_train = target_function(x_train)noise = torch.randn(y_train.shape) / 20.y_train = y_train + noisex_train.unsqueeze_(1)y_train.unsqueeze_(1)x_validation = torch.linspace(-10, 5, 100)y_validation = target_function(x_validation)x_validation.unsqueeze_(1)y_validation.unsqueeze_(1)# ------Dataset preparation end--------На рисунке 4 представлен результат обучения измененной нейронной сети.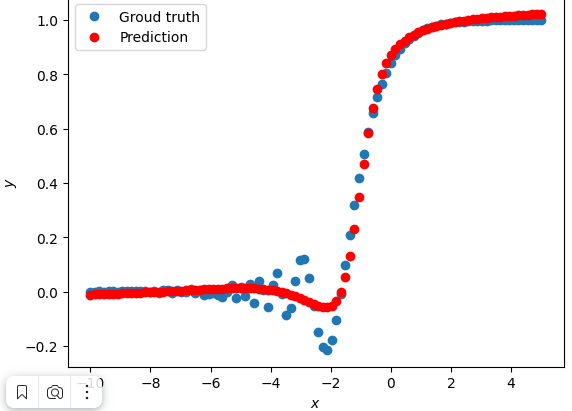Рисунок 4 - результат обучения измененной нейронной сети4. Для получения метрики код был изменен следующим образом:1. Добавлена функция получения метрики и вывод результата:def metric(pred, target): return (pred - target).abs().mean()print(metric(sine_net.forward(x_validation), y_validation).item())3. Изменено значение градиентного спуска lr=0.011, а также количество эпох уменьшено до 1000. 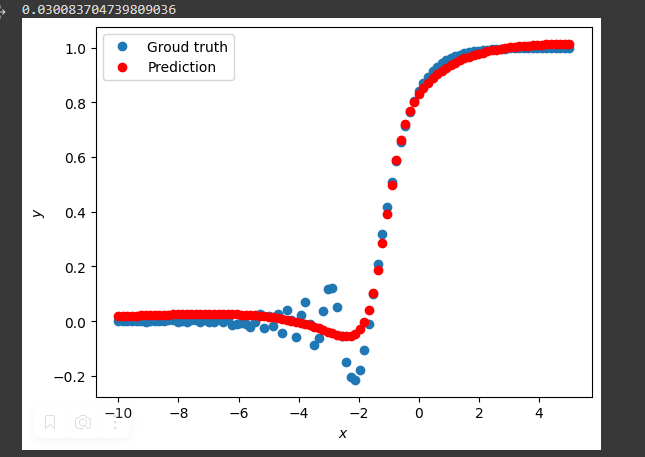На рисунке 5 представлен результат выполнения такого кодаРисунок 5 - Результат нахождения метрикиВывод: В ходе выполнения лабораторной работы были исследованы принципы разработки нейронной сети на примере задачи регрессии, получены навыки составления тренировочных и валидационных наборов данных, обучения нейросети, получения метрик.

---

Смотрите также файлы

• Кейс Тема решение кейса.docx

• Language in use read the article about language evolution and put the verbs in brackets in the correct form.docx

• Темаический план курс 2,семестр 4, группа тэо 21.docx

• Законодательство рф в области образования включает в себя.docx

• Хозяйственная политика Екатерины ii екатерина ii алексеевна.pptx