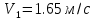Файл: Тема Основные теоремы динамики механической системы.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 26.10.2023

Просмотров: 27

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Практическое задание 9


Тема 3.3. Основные теоремы динамики механической системы

Задание

Механическая система в вертикальной плоскости (рис. 9.1) состоит из груза 1, ступенчатых шкивов 2 и 3 и катка 4 с радиусами: r2 = 0,2 (м); R2 = 0,4 (м); г3 = 0,3 (м); R3 = 0,4 (м); R4 = 0,5 (м). Радиусы инерции 2-го и 3-го тел: i2 = 0,3 (м); i3 = 0,33 (м). Коэффициент трения скольжения груза 1 о плоскость равен 0,1; коэффициент трения качения колеса 4 равен 0,002 (м). Система начинает движение из состояния покоя в направлении заданной силы F1, которая равна C + 1 (кН) (если П = 0… 2), или в направлении, обусловленном направлением вращения моментов M2, который равен C + 2 (кН·м) (если П = 3...5); М3, который равен С + 3 (кН·м) (если П = 6... 7), и М4, который равен С + 4 (кН·м) (если П = 8... 9). Определите скорость груза 1 в тот момент, когда его перемещение станет равным 0,1(Г + 1) (м), если массы тел следующие: масса первого тела Г + 2 (кг); второго 2Г + 1 (кг); третьего П + 2 (кг); четвертого ПГ + 1 (кг); углы: α равен 30 + 5П (град); β равен 80 – 5П (град).


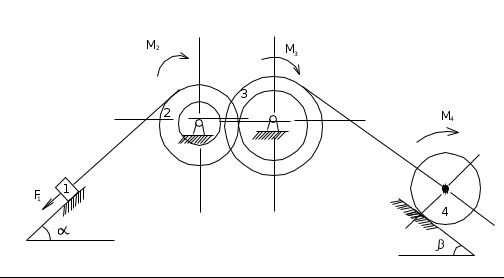
Рис. 9.1

Рекомендации по выполнению задания 9

  1. Выделите твердое тело или систему тел, движение которых рассматривается.

Расставьте внешние силы, действующие на тело или систему тел.

  1. Выделите тела связей.

Освободите тело от существующих связей, их действие замените реакциями связей.

  1. Покажите векторы скоростей и найдите центр тяжести тела.

  2. Постройте систему координат.

  3. Составьте уравнение, применяя одну из основных теорем динамики механической системы.

Решите полученное уравнение, определите неизвестную по условию величину.

Бланк выполнения задания 9


1. Записываются данные задания.

Механическая система в вертикальной плоскости (рис. 9.1) состоит из груза 1, ступенчатых шкивов 2 и 3 и катка 4 с радиусами: r2 = 0,2 (м); R2 = 0,4 (м); г3 = 0,3 (м); R3 = 0,4 (м); R4 = 0,5 (м). Радиусы инерции 2-го и 3-го тел: i2 = 0,3 (м); i3 = 0,33 (м). Коэффициент трения скольжения груза 1 о плоскость равен 0,1; коэффициент трения качения колеса 4 равен 0,002 (м). Система начинает движение из состояния покоя в направлении вращения моментов М
4, который равен 11 кН·м. Определите скорость груза 1 в тот момент, когда его перемещение станет равным 0,9 м, если массы тел следующие: масса первого тела 10 (кг); второго 17 (кг); третьего 10 (кг); четвертого 65 (кг); углы: α равен 70 (град); β равен 40 (град).

2. Представляется рисунок, на котором показаны все силы.



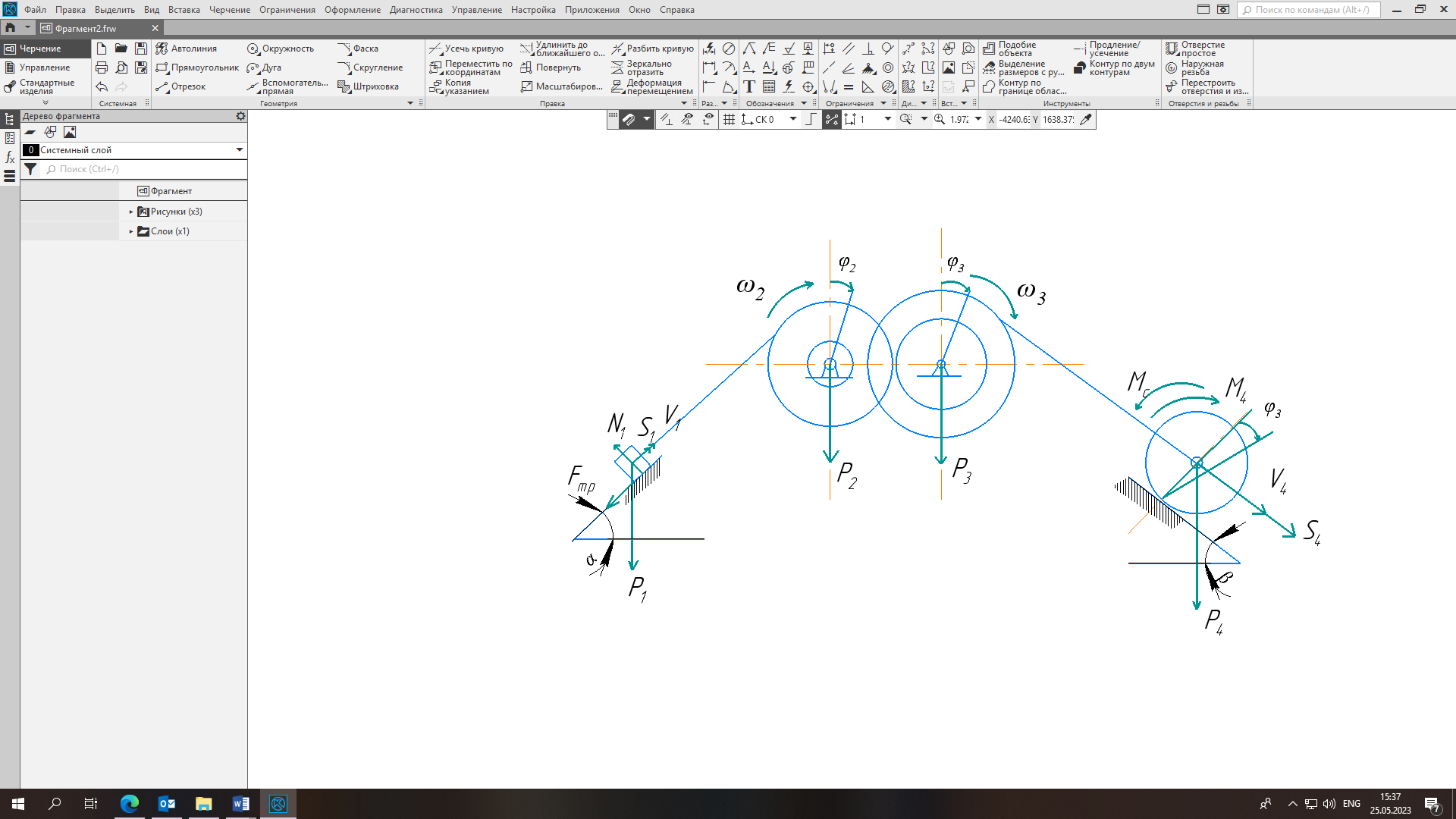
3. Записывается уравнение теоремы об изменении кинетической энергии механической системы.

Применим теорему об изменении кинетической энергии механической системы:





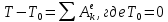
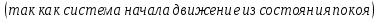
Кинетическая энергия механической системы





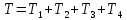
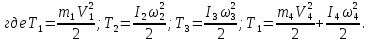
4. Решается уравнение.

Выразим 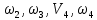через искомую скорость груза 1-V1.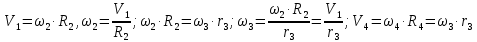





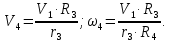
Моменты инерции тел 2,3,4



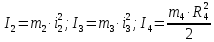
Определим кинетическую энергию системы





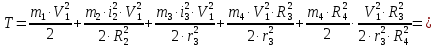
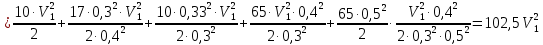
Определим сумму работ всех внешних сил:



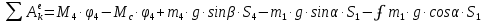
Где ;

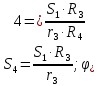Тогда



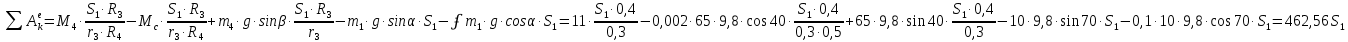
Приравняем кинетическую энергию и работу всех внешних сил, получим





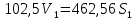
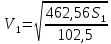
При



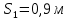
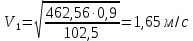
5. Записывается ответ.

Смотрите также файлы