Алгебра и начала анализа

10 класс

УМК: Алгебра и начала анализа 10-11 класс, А.Г. Мордкович, Москва 2013

Уровень обучения: базовый

Тема: Определение числовой функции и способы её задания.

Всего часов: 3

По теме: урок № 1

Цель урока:  

1. 
   Ввести и закрепить определения функции, области определения функции и графика функции.
   
2. 
   Развивать логическое мышление учащихся через формирование строить графики функций.
   
3. 
   Воспитывать графическую культуру учащихся.
   

Задачи урока:

1.Познакомить учащихся с числовой функцией и ее графиком.

2.Обогатить опыт учащихся в получении новых знаний на основе уже имеющихся теоретических знаний, а также через использование знакомых ситуаций практического характера

Планируемые результаты:

После изучения этой темы учащиеся должны знать:

• 
  Определение числовой функции и ее графика;
  
• 
  построение графика кусочной функции по ее частям;
  
• 
  примеры функций из жизни;
  
• 
  определение значения функции в любой точке;
  
• 
  приемы сравнения, обобщения, умение делать выводы;
  

После изучения этой темы учащиеся должны уметь:

• 
  - самостоятельно пополнять и систематизировать свои знания:
  
• 
  - строить графики функций:
  
• 
  - находить значения функции в любой точке.
  

Техническое обеспечение урока: учебное пособие «Алгебра и начала анализа. 10 класс (базовый уровень)» А.Г. Мордкович. Таблицы числовых функций.

Дополнительное методическое и дидактическое обеспечение урока:

Методическое пособие для преподавателей «Поурочные планы к учебнику Алгебра и начала анализа 10-11 класс», А.Г. Мордкович, Волгоград 2013

Интернет ресурсы

https://www.tutoronline.ru

Содержание урока:

1. 
   Организационный момент
   
2. 
   Повторение
   
3. 
   Изучение нового материала
   
4. 
   Закрепление
   
5. 
   Итог урока
   
6. 
   Постановка домашнего задания
   

---

Ход урока:

1.Орг.момент.

Учитель сообщает учащимся цель урока и средства ее достижения.

2. Повторение

- В различных сферах жизни мы нередко имеем дело со всевозможными соответствиями, т.е. правилами, по которым одним объектам (элементам) сопоставляются другие. Вот некоторые примеры таких соответствий.



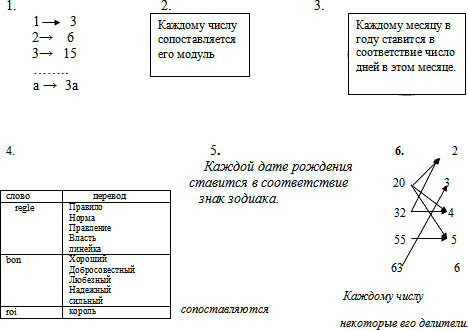
Все эти соответствия можно разделить на группы по различным признакам. Но есть среди них совершенно особенные, такие как 1, 2 и 5. Это такие соответствия, при которых каждому элементу одного множества сопоставляется единственный элемент другого множества. Такие соответствия и называются функциями.

3. Изучение нового материала.

- Что же такое функция?

Определение 1. Пусть даны два множества действительных чисел D и Е и указан закон f по которому каждому числу х ∈ D ставится в соответствие единственное числом y ∈ Е (см. рисунок). Тогда говорят, что задана функция у = f(x) или у(х) с областью определения (О.О.) D и областью изменения (О.И.) Е. При этом величину х называют независимой переменной (или аргументом функции), величину у - зависимой переменной (или значением функции).



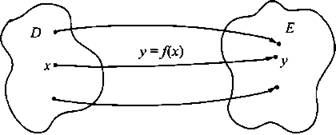
Область определения функции f обозначают D(f). Множество, состоящее из всех чисел f(x) (область значений функции f), обозначают E(f).

- Что такое график функции?

Определение 2. Если дана функция у = f(x) , хЄХ и на координатной плоскости хОу отмечены все точки вида (х; у), где х Є Х, а у = f (x), то множество этих точек называют графиком функции.

- Как выглядят графики некоторых функций?

у = kx+m y = ax² +bx +c y = k/x y = √x



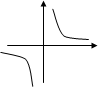
y = IxI



- На стр.5-7 учебника представлены примеры различных функций и их графиков.

- Рассмотрим функцию 

---

 Для нахождения у для каждого значения х необходимо выполнить следующие операции: из величины х вычесть число 2 (х - 2), извлечь квадратный корень из этого выражения   и, наконец, прибавить число 3   Совокупность этих операций (или закон, по которому для каждого значения х ищется величина у) и называется функцией у(х). Например, для х = 6 находим   Таким образом, для вычисления функции у в данной точке х необходимо подставить эту величину х в данную функцию у(х).

Очевидно, что для данной функции для любого допустимого числа х можно найти только одно значение у (т. е. каждому значению х соответствует одно значение у).

Рассмотрим теперь область определения и область изменения этой функции. Извлечь квадратный корень из выражения (х - 2) можно, только если эта величина неотрицательная, т. е. х - 2 ≥ 0 или х ≥ 2. Находим   Так как по определению арифметического корня   то прибавим ко всем частям этого неравенства число 3, получим:   или 3 ≤ у < +∞. Находим 

В математике часто используются рациональные функции. При этом функции вида f(x) = р(х) (где р(х) - многочлен) называют целыми рациональными функциями. Функции вида   (где р(х) и q(x) - многочлены) называют дробно-рациональными функциями. Очевидно, дробь   определена, если знаменатель q(x) не обращается в нуль. Поэтому область определения дробно-рациональной функции 

---

             - множество всех действительных чисел, из которого исключены корни многочлена q(x).

- А теперь рассмотрим рациональную функцию   . Она определена при х - 2 ≠ 0, т. е. x ≠ 2. Поэтому область определения данной функции - множество всех не равных 2 действительных чисел, т. е. объединение интервалов (-∞; 2) и (2; ∞).

Напомним, что объединением множеств А и В называется множество, состоящее из всех элементов, входящих хотя бы в одно из множеств А или В. Объединение множеств А к В обозначается символом АUВ. Так, объединением отрезков [1; 5] и (3; 9) является промежуток [1; 9). Объединение промежутков [1; 2) и [3; 4] (непересекающиеся промежутки) обозначают [1; 2) U [3; 4].

Возвращаясь к примеру, можно записать:   Так как при всех допустимых значениях х дробь   не обращается в нуль, то функция f(x) принимает все значения, кроме 3. Поэтому 

Мы уже встречали функции, заданные несколькими формулами, в зависимости от значений аргумента, например:

y={x–3,при x>3;
     {-(x – 3), при x < -3.

Такие функции называются кусочными или кусочно-заданными. Участки числовой прямой с различными формулами задания, назовем составляющими область определения. Объединение всех составляющих является областью определения кусочной функции. Те точки, которые делят область определения функции на составляющие, называются граничными точками. Формулы, определяющие кусочную функцию на каждой составляющей области определения, называются входящими функциями. Графики кусочно-заданных функций получаются в результате объединения частей графиков, построенных на каждом из промежутков разбиения.

Построить график кусочной функции (построение на доске)

---

1)       {-3, при -4 ≤ x < 0,
f(x) = {0, при x = 0,
          {1, при 0 < x ≤ 5.

График первой функции – прямая, проходящая через точку y = -3. Она берет свое начало в точке с координатами (-4; -3), идет параллельно оси абсцисс до точки с координатами

(0; -3). График второй функции – точка с координатами (0; 0). Третий график аналогичен первому – это прямая, проходящая через точку y = 1, но уже на участке от 0 до 5 по оси О

4.Закрепление изученного материала

Дана функция у = f(х), где

1. 
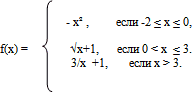
   Вычислить: 
   а) f( -2);
   б) f ( 0);
   в) f( 1, 25);
   г) f(6).
   
2. 
   Найти D (f) и E(f).
   
3. 
   Выяснить, сколько корней имеет уравнение f(х) =а при различных значениях а.
   
4. 
   Решить неравенства: 
   а) f(х) < 0,5;
   б) f(х) > 0,5.
   

Решение.

Дана кусочная функция.

1.

а) значение х=-2 удовлетворяет условию -2 ≤ х ≤ 0, значит f( -2) надо вычислять по формуле f(х) =- х²; f( -2) = -(-2)² ==-4.

б) значение х =0 удовлетворяет условию -2 ≤ х ≤ 0, значит f ( 0) надо вычислять по формуле f(х) =- х²; f ( 0) =-0² =0.

в) значение f( 1, 25) удовлетворяет условию 0 < х ≤ 3, значит f( 1, 25) надо вычислять по формуле f(х) = √х+1; f( 1, 25)= √1,25 +1 =1,5.

г) значение f(6) удовлетворяет условию х > 3, значит f(6) надо вычислять по формуле 3/х +1

f(6)=3:х +1= 3:6+1=1,5.

2. Область определения D (f) состоит из трех промежутков: [-2;0], (0;3], (3; +∞). Объединив их, получим луч [-2; +∞).

Чтобы найти область значений функции, построим ее график. Он состоит из трех кусочков заданной функции. Спроецировав этот график на ось у, получим область значений функции.

E(f)= [-4; 0]U( 1; 2]



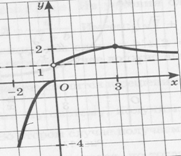
3. Выясним, сколько корней имеет уравнение f(х) =а при различных значениях а.

Для этого нужно определить, сколько точек пересечения имеет построенный график функции с прямой у=а при различных значениях параметра а.

1. 
   При -4 ≤ а≤ 0 прямая пересекается с графиком в одной точке. Значит, уравнение имеет 1 корень.
   
2. 
   При а< -4 корней нет.
   
3. 
   При 0<а ≤1 корней нет.
   
4. 
   При а>2 корней нет.
   
5. 
   При а=2  – 1 корень.
   
6. 
   При 1<а <2 два корня.
   

5. Итог урока.

• 
  Какое соответствиеназывается функцией?
  
• 
  Что такое область определения Х функции?
  
• 
  Дайте определение графика функции.
  

---

Смотрите также файлы

• Медицинская помощь и лечение. Лекарственная помощь как вид социального обеспечения.docx

• Введение Подсчет объемов земляного полотна.doc

• Эссе Важность знаний об индивидуальновозрастных особенностях развития обучающихся.docx

• План конспект проведения занятия по огневой подготовке с личным составом 7 мотострелковой роты на 2018 г. Тема 2 Стрелковое оружие, гранатометы и учебные стрелковые приборы занятие 1.rtf

• По учебному курсу Исследование рынка.docx