Основные законы механики жидкости и газа


Уравнение неразрывности

Для жидкости, текущей в трубе, этот закон используют в такой форме (называемой уравнением неразрывности):

v⋅S = const

Где v - скорость жидкости S - площадь сечения трубы, по которой течёт жидкость. Сформулировать этот закон можно и так:

Сколько вливается жидкости в ёмкость, в данном случае в трубу, столько должно и выливаться, если условия течения не изменяются.

Скорость в узких участках трубы должна быть выше, чем в широких.

Уравнение Бернулли стационарного движения

Одно из важнейших уравнений гидромеханики было получено в 1738 г. швейцарским учёным Даниилом Бернулли (1700 - 1782). Ему впервые удалось описать движение идеальной жидкости, выраженной в формуле Бернулли.
Идеальная жидкость - жидкость, в которой отсутствуют силы трения между элементами идеальной жидкости, а также между идеальной жидкостью и стенками сосуда.
Уравнение стационарного движения, носящее его имя, имеет вид:

P +ρ⋅v² + ρ⋅g⋅h = const 2

где P - давление жидкости, ρ − её плотность, v - скорость движения, g - ускорение свободного падения, h - высота, на которой находится элемент жидкости.

Смысл уравнения Бернулли в том, что внутри системы заполненной жидкостью (участка трубопровода) общая энергия каждой точками всегда неизменна.

В уравнении Бернулли есть три слагаемых:

ρ⋅v²/2 - динамическое давление - кинетическая энергия единицы объёма движущей жидкости;

ρ⋅g⋅h - весовое давление - потенциальная энергия единицы объёма жидкости;

P - статическое давление, по своему происхождению является работой сил давления и не представляет собой запаса какого-либо специального вида энергии ("энергии давления").

Это уравнение объясняет почему в узких участках трубы растёт скорость потока и падает давление на стенки трубы. Максимальное давление в трубах устанавливается именно в месте, где труба имеет наибольшее сечение. Узкие части трубы в этом отношении безопасны, но в них давление может упасть настолько

---

, что жидкость закипит, что может привести к кавитации и разрушению материала трубы.

Явление кавитации

Кавитация (от латинского cavitas - "углубление", "полость") - процесс образования полостей (пузырьков) в движущейся жидкости вследствие понижения давления.

Явление кавитации также объясняется уравнением Бернулли. Если скорость течения жидкости значительно возрастает, то давление сильно понизится - настолько, что жидкость закипит. Такую скорость можно получить, если пропускать жидкость через очень узкий участок трубы или при быстром обращении лопатки в водяном насосе.

Пузырьки по ходу движения жидкости попадают в области жидкости с нормальным давлением и там схлопываются. Это схлопывание сопровождается гидродинамическими эффектами, способными привести к разрушению трубы или стенок насоса.

Гидродинамика Эйлера и Навье-Стокса

Уравнение Бернулли позволяет объяснить очень много интересных гидродинамических явлений, но гораздо больше явлений, происходящих в движущихся жидкостях и газах, с его помощью объяснить нельзя, потому что этот закон для идеальной жидкости, т.е для жидкости, которая не обладает внутренним трением, а значит не создает гидравлическое сопротивление.

Реальная жидкость отличается от идеальной и обладает внутренним трением, или по-другому называют вязкостью. Два соприкасающиеся элемента жидкости, двигающиеся в одном и том же направлении, но с разными скоростями, воздействуют друг на друга. Сила взаимодействия ускоряет медленно движущийся элемент жидкости и замедляет более быстрый.

Закон вязкого трения Ньютона

Ньютон предположил, что величина этой силы (называемой силой внутреннего трения) пропорциональна разности скоростей элементов жидкости. Следовательно, сила внутреннего трения F пропорциональна изменению скорости жидкости v в направлении, перпендикулярном движению, и зависит от площади S соприкосновения элементов жидкости:

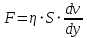
η − коэффициент динамической вязкости.

Жидкости, в которых внутреннее трение подобным образом зависит от изменения скорости, называются ньютоновскими, или жидкостями с линейной вязкостью.
Величину коэффициента динамической вязкости (и справедливость данного закона) Ньютон определил с помощью несложного опыта: он передвигал по поверхности жидкости пластинку с той или иной скоростью. Для того чтобы поддерживать эту скорость постоянной, требовалась сила, которая при небольшой глубине жидкости оказалась прямо пропорциональна площади S и скорости пластинки v и обратно пропорциональна глубине жидкости h:

---

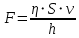
И хотя при увеличении глубины жидкости h сила вязкого трения пластинки не становится исчезающе малой, эта формула довольно точно описывает взаимодействие между соприкасающимися элементами жидкости.

Чем больше разность скоростей, тем больше сила, с которой они воздействуют друг на друга, заставляя притормаживать слишком быстро движущиеся элементы и разгоняя слишком медленные.

В результате относительное движение в жидкости прекращается (но иногда это может произойти не очень скоро).

Уравнение Навье - Стокса для вязких жидкостей

В более строгой формулировке линейная зависимость вязкого трения от изменения скорости движения жидкости называется уравнением Навье - Стокса. Оно учитывает сжимаемость жидкостей и газов и, в отличие от закона Ньютона, справедливо не только вблизи поверхности твёрдого тела, но и в каждой точке жидкости (у поверхности твёрдого тела в случае несжимаемой жидкости уравнение Навье - Стокса и закон Ньютона совпадают).



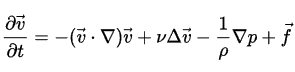
Любые газы, для которых выполняется условие сплошной среды, подчиняются и уравнению Навье - Стокса, т.е. являются ньютоновскими жидкостями.

Вязкость жидкости и газа обычно существенна при относительно малых скоростях, потому иногда говорят, что гидродинамика Эйлера — это частный (предельный) случай больших скоростей гидродинамики Навье - Стокса.

При малых скоростях в соответствии с законом вязкого трения Ньютона сила сопротивления тела пропорциональна скорости. При больших скоростях, когда вязкость перестаёт играть существенную роль, сопротивление тела пропорционально квадрату скорости (что впервые обнаружил и обосновал Ньютон).

Критерий Рейнольдса

Такую зависимость вывел английский физик и инженер Осборн Рейнольдс (1842 - 1912).

Критерий, который помогает ответить на вопрос, есть ли необходимость учитывать вязкость, является число Рейнольдса Re. Оно равно отношению энергии движения элемента текущей жидкости к работе сил внутреннего трения.

Рассмотрим кубический элемент жидкости с длиной ребра n. Кинетическая энергия элемента равна:

---

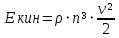
Согласно закону Ньютона, сила трения, действующая на элемент жидкости, определяется так:



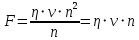
Работа этой силы при перемещении элемента жидкости на расстояние n составляет:

A = F⋅n = η⋅v⋅n²

а отношение кинетической энергии элемента жидкости к работе силы трения равно:

	Eкин	=	ρ⋅n³⋅v²
	A		2⋅η⋅v⋅n²

Сокращаем и получаем:

Re =	ρ⋅n⋅v
	2η

Re - называется числом Рейнольдса.

Таким образом, Re — это безразмерная величина, которая характеризует относительную роль сил вязкости.

Например, если размеры тела, с которым соприкасаются жидкость или газ, очень малы, то даже при небольшой вязкости Re будет незначительно и силы трения играют преобладающую роль. Наоборот, если размеры тела и скорость велики, то Re >> 1 и даже большая вязкость почти не будет влиять на характер движения.

Однако не всегда большие числа Рейнольдса означают, что вязкость не играет никакой роли. Так, при достижении очень большого (несколько десятков или сотен тысяч) значения числа Re плавное ламинарное (от латинского lamina - "пластинка") течение превращается в турбулентное (от латинского turbulentus - "бурный", "беспорядочный"), сопровождающееся хаотическими, нестационарными движениями жидкости. Этот эффект можно наблюдать, если постепенно открывать водопроводный кран: тонкая струйка течёт обычно плавно, но с увеличением скорости воды плавность течения нарушается. В струе, вытекающей под большим напором, частицы жидкости перемещаются беспорядочно, колеблясь, всё движение сопровождается сильным перемешиванием.

Появление турбулентности весьма существенно увеличивает лобовое сопротивление. В трубопроводе скорость турбулентного потока меньше скорости ламинарного потока при одинаковых перепадах давления. Но не всегда турбулентность плоха. В силу того что перемешивание при турбулентности очень значительно, теплообмен - охлаждение или нагревание агрегатов - происходит существенно интенсивнее; быстрее идёт распространение химических реакций.

---

2. 
   Термодинамика и ее основные законы
   

Предметом изучения термодинамики является изучение законов взаимных превращений различных видов энергии, связанных с переходами энергии между телами, чаще всего в форме теплоты и работы.

Термодинамическая система включает в себя рабочее тело и границу термодинамической системы.

Рабочее тело - макротело или совокупность тел, входящих в термодинамическую систему.

Граница термодинамической системы - может быть как реальной (резервуар), так и условной в виде контрольной поверхности.

Классификация термодинамических систем бывает следующих видов:

1) По виду рабочего тела;

2) По обмену энергией с окружающей средой;

3) По обмену с окружающей средой веществом.

Классификация термодинамических систем по виду рабочего тела:

1) Гомогенные – однородная система, химический состав и физические свойства которой во всех частях одинаковы или меняются непрерывно, без скачков (между частями системы нет поверхностей раздела).

2) Гетерогенные – системы, состоящие из нескольких разнородных веществ в различных агрегатных состояниях. Гомогенные части гетерогенной системы, отделенные от остальной её части видимыми границами, называют фазами.

Классификация термодинамических систем по обмену энергией с окружающей средой:

1) Термомеханическая - обменивается с окружающей средой энергией в форме теплоты и в форме работы;

2) Адиабатная - обменивается с окружающей средой энергией в форме работы (dQ = 0).

Классификация термодинамических систем по обмену веществом с окружающей средой:

1) Открытая система – система, которая обменивается веществом с окружающей средой;

2) Изолированная система – система, которая не взаимодействует с окружающей средой.

Существуют различные виды состояний термодинамической системы:

Равновесное состояние термодинамической системы - состояние, при котором параметры не меняются со временем, при этом постоянство параметров не обусловлено каким-либо процессом либо внешним воздействием.

Стационарное состояние термодинамической системы - постоянство параметров обусловлено каким-либо процессом.

Первый закон термодинамики — это закон сохранения энергии, распространенный на тепловые явления. Он формулируется следующим образом: 

---

Смотрите также файлы

• Специальность 49. 02. 02 Преподаватель Адаптивная физическая культура Фирсова А. В.pptx

• Закончившаяся для него тюрьмой и странной смертью, а для нее цыганским проклятием.pdf

• Диски со стрептомицином.docx

• Препараты для базисной.docx

• Презентация по психологии общения.pptx