Цилиндрические образцы исследуемого материала должны иметь достаточно большую длину по сравнению с диаметром. Однако при этом надо иметь в виду трудности, связанные со сверлением отверстий для заделки термопар по изотермическим поверхностям (в аксиальных направлениях). Поэтому удобнее изготовлять более короткие образцы в виде отдельных колец с неглубокими отверстиями для термопар. Но тогда образцы должны иметь надежную тепловую защиту с торцов, для того чтобы создать одномерность теплового потока, при которой аксиальные тепловые потоки становятся пренебрежимо малыми по сравнению с радиальными.

Защита торцевых поверхностей производится с помощью экранов, выполненных из фольги, тепловой изоляции или с помощью охранных электрических нагревателей.

Применение составных образцов из отдельных дисков позволяет также уменьшить аксиальные утечки тепла вследствие появления дополнительного контактного сопротивления между этими дисками.

Применение метода цилиндрического слоя связано с некоторыми трудностями:

1. Необходимость устранения потерь тепла с торцевых поверхностей и потребность в надежной центровке основного осевого нагревателя, создающего радиальный перепад температур в цилиндрическом слое исследуемого материала, которая требуется для создания равномерного обогрева внутренней поверхности образца.

2. Требуется компенсация удлинений, возникающих вследствие термического расширения нагревателя. Проволоку для нагревателя лучше наматывать на твердый стержень. Если для нагревателя используется тонкая нить, то она должна иметь пружинку или груз для компенсации удлинений. Если образец проводит электрический ток, то можно пропускать ток непосредственно через сам образец, но и в этом случае необходимо предусматривать устройства для компенсации теплового расширения образца и тоководов [3]. 1.2.

---

Конвективный теплообмен

Конвективный теплообмен занимает основное, центральное место в теории тепломассообмена.

Конвективный теплообмен – теплообмен, сочетающий конвекцию и теплопроводность, так как «чистая» конвекция без теплопроводности в реальной среде с йразными температурами невозможна.

Одним из основных моментов, подлежащих расчету является обмен теплотой между твердой поверхностностью и омывающей ее жидкостью (газом) – конвективная теплоотдача или просто теплоотдача. В практических расчетах используют формулу Ньютона-Рихмана:

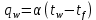1.3

где qw – плотность теплового потока через поверхность, Вт/м²; t_w, t_f – соответственно, температуры поверхности и среды, К;  – коэффициент теплоотдачи, Вт /(м² К) .

Величина коэффициента теплоотдачи  зависит от свойств жидкости и характера ее движения, но не зависит от теплофизических свойств твердого тела.

Формула (1.3) – основное соотношение теории конвективного теплообмена. В отличие от закона Фурье это не столько решение, сколько формулировка проблемы, так как основной целью исследований является определение величины коэффициента теплоотдачи .

Различают вынужденную и свободную конвекцию.

Вынужденная конвекция – движение среды происходит под действием приложенного перепада давления или инерции, т. е. причины движения прямо не связаны с процессом теплообмена. Например, движение под действием насоса, вентилятора, ветра и т. п.

Свободная конвекция – когда движение среды происходит за счет неоднородности массовых сил, возникающей вследствие неравномерного нагрева, без внешних поверхностных сил, т. е. без приложенного перепада давления. Обычный случай свободной конвекции – движение за счет различия удельных весов нагретой или холодной жидкости, так называемая естественная или свободная гравитационная конвекция. При этом нагретая жидкость или газ расширяются, становятся легче и поднимаются вверх, вызывая общее движение. Но может быть свободная конвекция в поле центробежных сил, а также сил иной природы – магнитных и др.

Возможно, сочетание вынужденного и свободно-конвективного движения. При больших скоростях вынужденного движения свободноконвективная составляющая незначительна, и ей можно пренебрегать [2].

---

В современном учении о конвективном теплообмене принято обрабатывать данные эксперимента в виде безразмерных комплексов, называемых числами подобия. Эта обработка позволяет распространять опытные данные исследуемого явления на группу ему подобных.

Тепловое излучение

Теплообмен излучением (радиационный теплообмен) является одним из трех простых видов теплообмена, наряду с теплопроводностью и конвекцией. Тепловое излучение свойственно всем телам, и каждое из них излучает энергию в окружающее пространство. При попадании на другие тела эта энергия частью поглощается, частью отражается и частично проходит сквозь тело. Та часть лучистой энергии, которая поглощается телом, снова превращается в тепловую. Часть энергии, которая отражается, попадает на другие окружающие тела и ими поглощается. То же самое происходит и с той частью энергии, которая проходит сквозь тело. Таким образом, после поглощения лучистая энергия полностью распределяется между окружающими телами. Следовательно каждое тело не только непрерывно излучает, но и непрерывно поглощает лучистую энергию. В результате этих явлений и осуществляется процесс лучистого теплообмена. Количество отдаваемой или воспринимаемой теплоты определяется разностью между количествами излучаемой и поглощаемой телом лучистой энергии. Такая разность отлична от нуля, если температура тел, участвующих во взаимном обмене лучистой энергией, различна.

При одинаковой температуре этих тел вся система находится в так называемом подвижном тепловом или термодинамическом равновесии. В этом случае все тела системы также излучают и поглощают, только для каждого из них приход лучистой энергии равен ее расходу.

Суммарное излучение, проходящее через произвольную поверхность F в единицу времени, называется потоком излучения Q. Лучистый поток, испускаемый с единицы поверхности по всем направлениям пространства, называется плотностью потока излучения E, Вт/м² :

E=dQ/dF 1.4

Пусть из всего количества энергии Q падающей на тело, часть QA поглощается, часть QR отражается и часть QD проходит сквозь тело (рис. 1.1), так что



Если все составляющие уравнения (1.10) поделить на Q, получим:

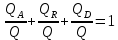1.6

A+R+D=0 1.7

где Q_A/ Q=A – поглощательная способность тела, равная доле падающего излучения поглощенного телом; Q

---

_R/Q=R– отражательная способность тела, равная доле падающего излучения отраженного телом; Q_D/Q=D – пропускательная способность тела, равная доле падающего излучения проходящего через тело.

Если A = 1, то A = 0 и D = 0. Это означает, что вся падающая энергия поглощается телом и такие тела называют абсолютно черными (АЧТ). Понятие абсолютно черного тела – идеализированное, так как в природе и технике нет абсолютно черных тел. Все реальные тела – «серые» (A < 1).

Если R = 1, то А = 0 и D = 0. Это означает, что вся падающая энергия полностью отражается телом. При этом если отражение правильное (по законам геометрической оптики), то такие тела называются зеркальными, а если диффузное – абсолютно белыми.

Если D = 1, то А = 0 и R = 0. Это означает, что вся падающая энергия полностью проходит через тело. Такие тела называются абсолютно прозрачными (диатермичными).

Значения A, R и D зависят от природы тела, состояния поверхности, температуры тела. Большинство твердых тел и некоторые жидкости являются непрозрачными, т. е. D = 0. В этом случае A+R 1.

Рассмотрим теперь основные законы теплового излучения. В данных законах рассматривается абсолютно черное тело. Характеристики теплового излучения абсолютно черного тела в вакууме помечаются индексом «0». В полную формулировку законов может входить показатель преломления среды п (n 1 – для вакуума). Значение показателя преломления газов отличается от значения для вакуума на тысячные и десятитысячные, и, следовательно, этим отличием в практических расчетах можно пренебрегать. Так как при исследовании явления теплообмена в прозрачной среде приходится иметь дело с газами, то п в формулы не включают, но в более плотной среде его значение следует учитывать

Закон Планка. Для детального изучения явления важно знать закон распределения лучистой энергии по длинам волн при различных температурах. Величина E равная отношению плотности потока излучения, испускаемого в интервале длин волн от  до   d к рассматриваемому интервалу длин волн называется спектральной плотностью потока излучения, Вт/м³:

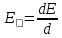1.8

Зависимость спектральной плотности потока излучения абсолютно черного тела от длины волны и температуры Планк установил теоретически на основе положений квантовой теории света:

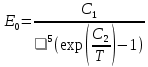1.9

При 0 плотность потока также стремится к нулю. С увеличением  растет E0 и при некотором значении max достигает своего максимума, затем убывает и при   снова стремится к нулю. С увеличением температуры потока максимум спектральной плотности потока излучения смещается в сторону более коротких волн.

---

Закон Вина (смещения) устанавливает связь между длиной волны максимального излучения max и температурой Т:

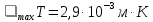1.10

площадь, ограниченная кривой T  const, осью абсцисс и ординатами  и   d (заштрихованная область), дает количество энергии, излучаемое участком длин волн d . Следовательно, dE₀=E₀d. Тогда полное количество энергии, излучаемое всеми длинами волн равно:

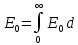1.11

Закон Стефана-Больцмана (закон четвертых степеней) был установлен опытным путем Стефаном (1879 г.), а теоретически обоснован Больцманом (1881 г.). Закон устанавливает, что поверхностная плотность потока излучения E0 пропорциональна четвертой степени Т:

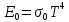1.12

где  5,67*10^-8 – постоянная Стефана-Больцмана, Вт/ (м² К⁴) .

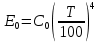1.13

где С₀ 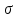 ₀  10⁸ =5,67 – коэффициент излучения абсолютно черного тела, Вт/(м² К) . Также этот закон может быть применен и к реальным телам. В этом случае уравнение (1.13) примет вид:

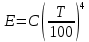1.14

У реальных тел энергия собственного излучения всегда меньше, чем у абсолютно черных. Сопоставляя плотность потока собственного излучения тела с плотностью потока абсолютно черного тела при той же температуре, получаем еще одну характеристику, которая называется степенью черноты  0<<1):

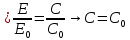1.15

Тогда уравнение (1.14) перепишется в виде:



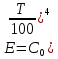
Степень черноты характеризует интегральное излучение тела, охватывающее все длины волн. Более детальной характеристикой тела является спектральная степень черноты:

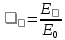1.16

Для серого излучения .

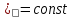На основании закона Стефана–Больцмана можно записать расчетную формулу лучистого теплообмена между двумя серыми телами заданной формы и размеров с температурами T1 и T2 , разделенными прозрачной средой (воздухом:

---

Смотрите также файлы

• Специальность 49. 02. 02 Преподаватель Адаптивная физическая культура Фирсова А. В.pptx

• Закончившаяся для него тюрьмой и странной смертью, а для нее цыганским проклятием.pdf

• Диски со стрептомицином.docx

• Препараты для базисной.docx

• Презентация по психологии общения.pptx