Файл: Задача 1 3 Задача 2 4 Задача 1 Дано По данным за период 20192021 гг динамика представлена в таблице.docx
Добавлен: 29.10.2023
Просмотров: 150
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическое задание 3Тема 3. Цикличность экономического развития, экономический рост, безработица и инфляция
Задача 1 3
Задача 2 4
, темп прироста капитала , темп прироста общефакторной производительности . Какой будет темп прироста объема выпуска ? Значения , , и производственная функция выбирают в соответствии с вариантом (таблица 5).Таблица 5 – Значения , , и производственная функция
Задача 2Дано:Экономический рост в модели Солоу задается производственной функцией , имеющая постоянную отдачу от увеличения масштаба производства. Темп прироста населения , темп прироста капитала , темп прироста общефакторной производительности . Какой будет темп прироста объема выпуска ?Решение:В неоклассической модели роста была использована производственная функция вида Y=AF(K,L). Объём производства Y зависит от вклада его факторов – труда L и капитала К, а также от технологии. Производственная функция имеет постоянную отдачу от масштаба, т.е. увеличение всех факторов в определенной степени приводит к росту выпуска в той же степени (если факторы увеличились вдвое, то выпуск возрастет также в 2 раза). Изменение выпуска можно представить как ∆Y=F(K,L)*∆A+MPK*∆K+MPL*∆L, где МРК и MPL – предельные производительности соответствующих факторов производства.Разделим это выражение на Y =A*F(K,L) и получим:Второе и третье слагаемое правой части уравнения умножим и разделим, соответственно, на К и L:В скобках представлены доли капитала и труда в общем объёме выпуска. При условии постоянной отдачи от масштаба сумма этих долей равна единице (по теореме Эйлера), тогдагде α – доля капитала;(1 – α) – доля труда в доходе;А – общая производительность факторов, мера уровня технологического прогресса, измеряемая обычно по остаточному принципу («остаток Солоу»)В представленной функции показатели степени представляют и долю факторов в доходе, то есть , что можно проверить математически, проведя с этой функцией все указанные выше операции.
Тогда То есть выпуск растет с темпом 4,15% % в год.
Оглавление
Задача 1 3
Задача 2 4
Задача 1
Дано: По данным за период 2019-2021 гг. динамика представлена в таблице.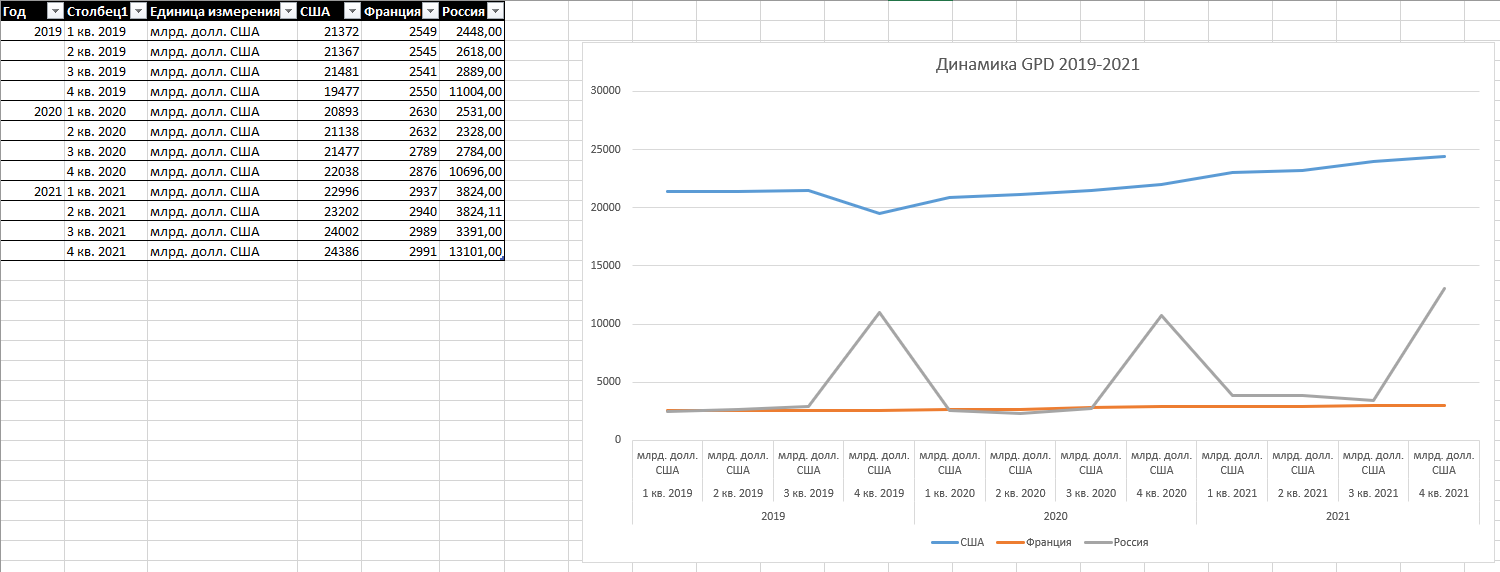Вывод: На ВВП США (22.9 трлн $) приходится примерно 25% мировой экономики, доли, которая на самом деле изменилось значительно за последние 60 лет. Финансы, страхование и недвижимость (4,7 триллиона долларов) вносят наибольший вклад в экономику страны, за ними следуют профессиональные и деловые услуги (2,7 триллиона долларов) и правительство (2,6 триллиона долларов).Экономика Китая занимает второе место в номинальном выражении с ВВП около 17 триллионов долларов. Она остается крупнейшим производителем в мире по объему производства, включая, в частности, производство стали, электроники и робототехники.Крупнейшей экономикой Европы является Германия, которая экспортирует примерно 20% автомобилей в мире. В 2019 году общий объем торговли составил почти 90% ВВП страны.Задача 2
Экономический рост в модели Солоу задается производственной функцией 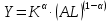,где 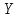– реальный ВВП, 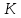– капитал, 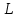– труд, 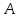– общефакторная (совокупная) производительность факторов, 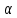– доля дохода капитала в национальном доходе, 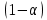- доля дохода труда в национальном доходе.Производственная функция имеет постоянную отдачу от увеличения масштаба производства. Темп прироста населения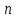, темп прироста капитала 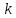, темп прироста общефакторной производительности 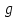. Какой будет темп прироста объема выпуска 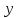? Значения 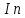, , 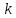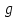и производственная функция выбирают в соответствии с вариантом (таблица 5).Таблица 5 – Значения 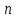, , 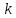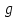и производственная функция
| Вариант | Показатель | |||
| производственная функция  | Темп прироста населения 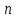 | Темп прироста капитала 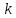 | Темп прироста общефактороной производительности  | |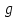
| 1 | 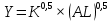 | 1,2 | 1 | 2 |
| 2 | 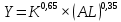 | 2 | 2 | 1 |
| 3 | 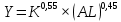 | 1,4 | 1,2 | 2,4 |
| 4 | 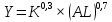 | 0,5 | 1,6 | 1,2 |
| 5 | 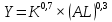 | 1 | 1,5 | 0,8 |
| 6 | 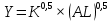| 1,4 | 2 | 1 |
| 7 | 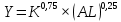 | 2 | 1 | 1,2 |
| 8 | 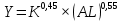 | 1 | 1,3 | 1,6 |
| 9 | 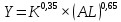 | 2 | 1,6 | 2,4 |
| 10 | 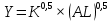| 1,4 | 1 | 0,8 |
Задача 2Дано:Экономический рост в модели Солоу задается производственной функцией , имеющая постоянную отдачу от увеличения масштаба производства. Темп прироста населения , темп прироста капитала , темп прироста общефакторной производительности . Какой будет темп прироста объема выпуска ?Решение:В неоклассической модели роста была использована производственная функция вида Y=AF(K,L). Объём производства Y зависит от вклада его факторов – труда L и капитала К, а также от технологии. Производственная функция имеет постоянную отдачу от масштаба, т.е. увеличение всех факторов в определенной степени приводит к росту выпуска в той же степени (если факторы увеличились вдвое, то выпуск возрастет также в 2 раза). Изменение выпуска можно представить как ∆Y=F(K,L)*∆A+MPK*∆K+MPL*∆L, где МРК и MPL – предельные производительности соответствующих факторов производства.Разделим это выражение на Y =A*F(K,L) и получим:Второе и третье слагаемое правой части уравнения умножим и разделим, соответственно, на К и L:В скобках представлены доли капитала и труда в общем объёме выпуска. При условии постоянной отдачи от масштаба сумма этих долей равна единице (по теореме Эйлера), тогдагде α – доля капитала;(1 – α) – доля труда в доходе;А – общая производительность факторов, мера уровня технологического прогресса, измеряемая обычно по остаточному принципу («остаток Солоу»)В представленной функции показатели степени представляют и долю факторов в доходе, то есть , что можно проверить математически, проведя с этой функцией все указанные выше операции.
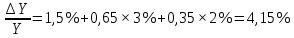
Тогда То есть выпуск растет с темпом 4,15% % в год.