Файл: Контрольная работа по дисциплине Основы статистики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 26
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
  К Г Э У | МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Федеральное государственное образовательное учреждение высшего образования «КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ЭНЕРГЕТИЧЕСКИЙ УНИВЕРСИТЕТ» |
Кафедра
Контрольная работа
по дисциплине «Основы статистики»
Выполнил студент:
Группа ЗРСО--21
Проверил преподаватель:
Казань – 2023
№1
| № | Левая | Правая | Частоты fi | 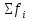 | 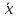 | 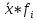 |
| 1 | 19953.00 | 28613.00 | 28 | 28 | 24283.00 | 679924.00 |
| 2 | 28613.00 | 37273.00 | 6 | 34 | 32943.00 | 197658.00 |
| 3 | 37273.00 | 45933.00 | 3 | 37 | 41603.00 | 124809.00 |
| 4 | 45933.00 | 54593.00 | 1 | 38 | 50263.00 | 50263.00 |
| 5 | 54593.00 | 63253.00 | 0 | 38 | 58923.00 | 0.00 |
| 6 | 63253.00 | 71913.00 | 1 | 39 | 67583.00 | 67583.00 |
| Итог | | | 39 | | | 1120237.00 |
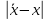 | 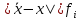 | 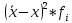 |
| 4441.03 | 124348.72 | 552235844.84 |
| 4218.97 | 25313.85 | 106798467.85 |
| 12878.97 | 38636.92 | 497603941.62 |
| 21538.97 | 21538.97 | 463927416.44 |
| 30198.97 | 0.00 | 0.00 |
| 38858.97 | 38858.97 | 1510019888.23 |
| | 248697.44 | 3130585558.97 |
Данные для расчетов интервалов групп:
Число единиц совокупности N = 39
Размах вариации R= Xmax - Xmin = 51955 руб
Число групп по формуле Стерджесса n = 1+3.322LgN = 6.285516625 = 6 групп
Ширина равного интервала h = R/n = 8660 руб
-
Среднее, модальное и медианное значение.
Модальное значение = 24802.6 руб
Медианное значение = 25984.1 руб
Среднее значение = 28724.0 руб
-
Показатели вариации: абсолютные
Размах = 51955.0 руб
Среднее линейное отклонение =6376.9 руб
Дисперсия = 80271424.6 (руб)2
Среднее квадратичное = 8959.4 руб
Оценка среднеквадратического отклонения = 9076.6 руб
Показатели вариации: относительные
Коэффициент вариации = 31.191%
Коэффициент осцилляции = 180.876%
Линейный коэффициент вариации = 22.20 %
-
Доверительный интервал
Ф(tkp) = 0.477
tkp(γ) = tkp (0.4985) = 2
Стандартная ошибка выборки для среднего: Sc = 1453.411 руб
Предельная ошибка выборки: ε = tkp * sc = 2906.82 руб
Доверительный интервал ( 25817.20 руб; 31630.84 руб)
-
Гистограмма и функция распределния для интервального ряда
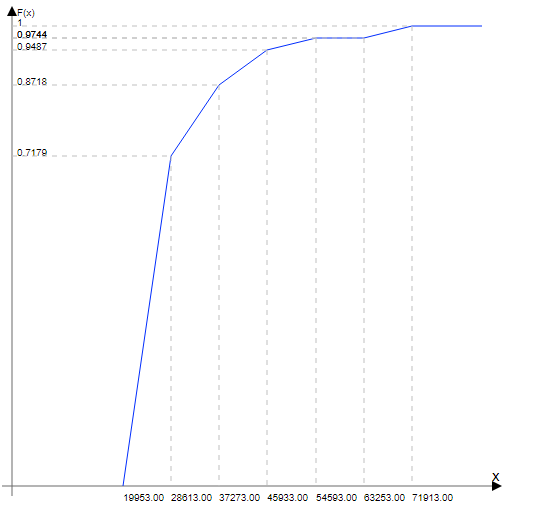
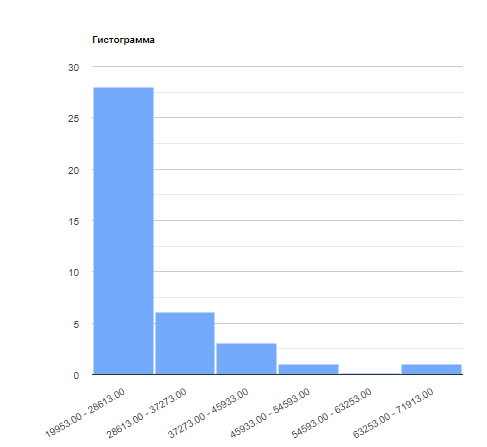
Выводы из полученных данных:
-
Каждое значение ряда отличается от среднего значения 28724.026 в среднем на 8959.432. -
Среднее значение отличается от медианного, поэтому ряд можно охарактеризовать как умеренно асимметричный. -
Поскольку коэффициент вариации находится в пределах [30%; 70%], то вариация умеренная.
№2
-
В качестве уравнения тренда выбираем линейную функцию.
| Год | t | y | t^2 | y^2 | ty | Теор знач | |
| 2010 | -5 | 21952 | 25 | 481890304 | -109760 | 21339.90476 | 374660.58 |
| 2011 | -3 | 23369 | 9 | 546110161 | -70107 | 24095.07619 | 527186.634 |
| 2012 | -1 | 26629 | 1 | 709103641 | -26629 | 26850.24762 | 48950.5089 |
| 2013 | 1 | 29792 | 1 | 887563264 | 29792 | 29605.41905 | 34812.4518 |
| 2014 | 3 | 32495 | 9 | 1055925025 | 97485 | 32360.59048 | 18065.9201 |
| 2015 | 5 | 35130 | 25 | 1234116900 | 175650 | 35115.7619 | 202.723356 |
| Итог | 0 | 169367 | 70 | 4914709295 | 96431 | 169367 | 1003878.82 |
Найденные коэффициенты линейной модели методом МНК
A = 1377.585714, B = 28227.83333
Полное уравнение тренда:
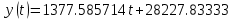
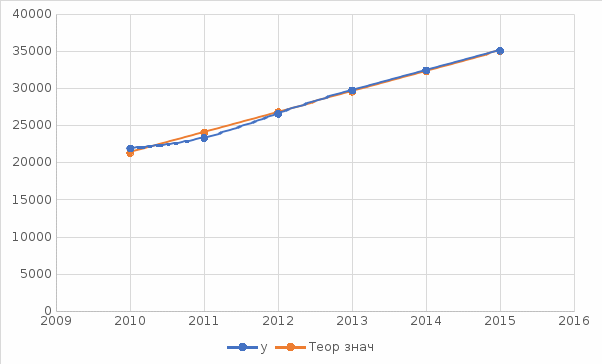
-
Доверительный интервал
Степень свободы: v = 4
Cреднее квадратическое отклонение от тренда: Sy = 500.97 тыс.человек
Точечный прогноз на 2023 год: y(21) = 54401.96 тыс.человек
Для доверительной вероятности 99%: а = 0.01
Коэффициент Стьюдента: t = 4.60
Доверительный интервал : ( 52095.45; 56708.47) тыс.человек
№3:
Таблица для вычисления коэффициента Фехнера
| Xi | Yi | Знаки отклонений от средней X | Знаки отклонений от средней Y | Совпадение (а) или несовпадение (b) знаков |
| 34 | 45 | - | - | A |
| 90 | 100 | + | + | A |
| 70 | 60 | + | - | B |
| 80 | 120 | + | + | A |
| 100 | 90 | + | + | A |
| 50 | 35 | - | - | A |
| 44 | 30 | - | - | A |
| 70 | 112 | + | + | A |
| 40 | 63 | - | - | A |
| 50 | 80 | - | + | B |
| 628 | 735 | | | |
Средние значения: x = 62.8 y = 73.5
Коээфициент Фехнера: 0.6
-
Упорядочим данные по X. В ряду Y справа от 3 расположено 7 рангов, превосходящих 3, следовательно, 3 породит в Р слагаемое 7.Справа от 5 стоят 5 ранга, превосходящих 5 (это 6, 9, 10, 8, 7), т.е. в Р войдет 5 и т.д. В итоге Р = 34 и с использованием формул имеем:
Таблица для вычисления коэффициента Кенделла
| X | Y | ранг X, dx | ранг Y, dy | P | Q |
| 34 | 45 | 1 | 3 | 7 | 2 |
| 40 | 63 | 2 | 5 | 5 | 3 |
| 44 | 30 | 3 | 1 | 7 | 0 |
| 50 | 35 | 4 | 2 | 6 | 0 |
| 50 | 80 | 5 | 6 | 4 | 1 |
| 70 | 60 | 6 | 4 | 4 | 0 |
| 70 | 112 | 7 | 9 | 1 | 2 |
| 80 | 120 | 8 | 10 | 0 | 2 |
| 90 | 100 | 9 | 8 | 0 | 1 |
| 100 | 90 | 10 | 7 | 0 | 0 |
| | | | | 34 | 11 |
Коээфициент Кенделла: 0.51
-
Присвоим ранги признаку Y и фактору X.
| X | Y | ранг X, dx | ранг Y, dy |
| 34 | 45 | 1 | 3 |
| 90 | 100 | 9 | 8 |
| 70 | 60 | 6 | 4 |
| 80 | 120 | 8 | 10 |
| 100 | 90 | 10 | 7 |
| 50 | 35 | 4 | 2 |
| 44 | 30 | 3 | 1 |
| 70 | 112 | 6 | 9 |
| 40 | 63 | 2 | 5 |
| 50 | 80 | 4 | 6 |