Файл: Контрольная работа. Вариант 6 Небольсина В. В. Институт онлайн образования.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 29.10.2023

Просмотров: 502

Скачиваний: 21

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Федеральное государственное образовательное бюджетное учреждение высшего образования
«Финансовый университет при Правительстве

Российской Федерации»

Департамент анализа данных, принятия решений и финансовых технологий

Контрольная работа. Вариант 6

Выполнила:

Небольсина В.В.

Институт онлайн образования

Аудит корпоративной безопасности

ДЭАКБ22-1м

e-mail: 228746@edu.fa.ru

Москва 2023

Контрольная работа

Вариант № 6


  1. Ссуда 350 000 руб. выдана на 4 года под 23% годовых (простые проценты). Во сколько раз больше наращенная сумма по сравнению со ссудой?

Решение:

  1. Используем формулу для определения наращенной суммы (простые проценты): Sn = S0 *(1+ i *n)

S0 – сумма ссуды; Sn – наращенная сумма; i – годовая ставка; n – число лет.

  1. Подставляем: Sn =350 000*(1+ 0,23*4) =672 000 руб.

  2. Увеличение составит: 672 000/350 000= 1,92 раза.

Ответ: 1,92 раз.



  1. Номинальная процентная ставка составляет 12% годовых при годовом темпе инфляции 4%. Чему равна годовая ставка с учётом инфляции? Чему равна эффективная реальная процентная ставка, если проценты начисляются ежемесячно? ежедневно? ежеквартально?

Решение:

  1. Реальную годовую ставку с учетом инфляции определим по формуле:

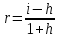, где i - номинальная процентная ставка; h - темп инфляции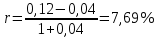



  1. Эффективная процентная ставка вычисляется по простой формуле: r = (1 + i/n)^n - 1.

Ежемесячно r = (1+0,0769/12)^12 - 1 = 7,967%

Ежедневно r = (1+0,0769/365)^365 – 1 = 7,993%

Eжеквартально r = (1+0,0769/4)^4 – 1 = 7,915%

Ответ:

Ежемесячно = 7,967%

Ежедневно = 7,993%

Eжеквартально = 7,915%



  1. Клиент поместил в банк вклад в сумме 1 800 000 руб. под 8% годовых с ежемесячной выплатой процентов. Какую сумму клиент будет получать каждый месяц, если начисление производится по формуле простых процентов?

Решение:

  1. Определим по формуле I = P * j* n 

  2. Подставляем:

I = 1 800 000 * 0,08 * 1/12 = 12 000 руб.

Ответ: 12 000 руб.



  1. Месячный темп инфляции составляет 2%. Найти индекс цен и темп инфляции за год, определить реальную наращенную сумму с учётом инфляции, если на сумму 1 500 000 руб. в течение года начислялась простая процентная ставка 15% годовых (К=360).

Решение:

  1. Темп инфляции за год равен: а = (1 + 0,02)^12 – 1 = 26,82%

  2. Индекс цен = 1,26

  3. Наращенная сумма равна 1 500 000 * 1,15 = 1 725 000 руб.

  4. В случае сложных процентов месячная ставка равна (1 + 0,15)^(1/12) - 1 = 1,17%

  5. Годовая ставка, при которой потери из-за инфляции равны наращению составит 26,82 %




  1. Фонд создается в течение 10 лет. Средства поступают в фонд в конце года равными суммами. На собранные средства в конце года начисляется 10% годовых. На сколько процентов возрастет наращенная сумма фонда при переходе к взносам в конце каждого квартала? Ответ привести с точностью до 0,01%.

Решение:

  1. Определим коэффициент наращения для каждого способа начисления процентов по формуле: r = [(1 + j / m)^(n * m) - 1] / [(1 + j / m)^(m) – 1] =

где j – номинальная процентная ставка ренты , m и p число периодов начисления процентов и платежей в году, n – число лет.

  1. Подставляем: r = ((1 + 0,1/4)^(10*4) - 1) / ((1 + 0,1/4)^(4) - 1) = 16,2317399

Ответ: 16,23%



  1. Найти срок ренты постнумерандо, если наращенная сумма равна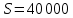 ; процентная ставка равна 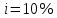; рентный платёж равен .

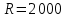Решение:

  1. Определим по формуле:



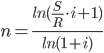
  1. n = ln ((40 000/2 000) * 0,1 + 1) / ln (1 + 0,1) = ln (3) / ln (1,1) = 11,5 лет

Ответ: 11,5 лет.



  1. Какую сумму нужно положить в банк под 10% годовых мужчине 52 лет, чтобы по достижении им пенсионного возраста 60 лет в течение 15 лет в начале каждого месяца снимать по 10 000 рублей, если проценты капитализируются в конце каждого месяца?

Решение:

R – сумму, нужную положить в банк; S – наращенная сумма по достижении им пенсионного возраста 60 лет. А = S

  1. Капитализация в конце месяца:

А = 10 000 * (1 - (1 + 0,10/12)^(–15*12) ) * (1 + 0,10/12)^ (12/12)/((1 + 0,10/12)^(12/12) –1) = 938 329,17

  1. S = R * (1 + 0,1/12)^(60– 52)*12 = R * (1 + 0,01)^96 = 2,60

  2. R = S / (1 + 0,01)^96 = S / 2,60 = 938329,17 / 2,60 = 360 996,79

Ответ: 360 996,79


  1. Рыночная цена 10-ти процентной облигации номиналом 2000 руб. за три года до погашения равна 2500 руб. найти текущую стоимость облигации при процентной ставке 9% и её курс.

Решение:

  1. С = 10% = 0,1, N = 2 000 руб., n = 3 года, V = 2 500 руб., г = 9% Найти: К, Р

  2. Найдем курс по формуле: К = V/N = 2 500 / 2 000 = 125 %

  3. Текущая стоимость Р вычисляется по формуле:



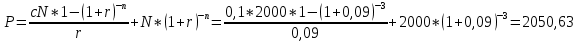
Ответ:

К= 125%

Р= 360 996,79



  1. Заемщик должен уплатить 80 000 руб. через 75 дней. Кредит выдан под 29% годовых (простые проценты). Какова первоначальная сумма долга и дисконт (К=360)?

Решение:

  1. Определим первоначальную сумму по формуле: P = S / (1 + in)

  2. Подставляем: S = 80 000 / (1 + 75/360 *0,29) = 75 442,04 руб.

  3. Дисконт равен D = 80 000 – 75 442,04 = 4 557,96 руб.

Ответ:

S = 75 442,04 руб.

D = 4 557,96 руб.



  1. В банк положен депозит в размере 2 400 руб. под 7% годовых по схеме сложных процентов. Найти величину депозита через три года при начислении процентов 4 раз в году.

Решение:

  1. S = 2 400 * ( 1 + 0,07/4)^(4*3) = 2 955,45 руб.

Ответ: 2 995,45 руб.



  1. Портфель состоит из двух ценных бумаг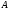 и 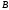, ожидаемая доходность и риск которых, выраженные в процентах, равны 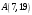, 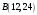. Коэффициент корреляции бумаг равен 1. Найти множество допустимых портфелей, построить график. Определить доходность портфеля минимального риска.

Решение:

  1. Риск портфеля, состоящий из двух активов, рассчитывается по формуле:



Таким образом, целевая функция σp → min

При следующих ограничениях:

— по составу портфеля θa + θb = 1,

— удельные веса не должны быть отрицательны.

  1. Определяем доходность портфеля минимального риска. В случае положительной корреляции, для того, чтобы получить портфель с минимальным риском, необходимо коротко продать один из активов, и инвестировать все имевшиеся и вырученные за счет короткой продажи средства во второй актив.

Поскольку коэффициент корреляции бумаг равен 1, то: где σ – уровень риска той или иной ценной бумаги.

Отсюда:

Доля А = 0,24 / (0,24 - 0,19) = 4,8

Доля В = 0,19 / (0,19 - 0,24) = - 3,8

То есть, доля рисковых бумаг В изначально должна составлять 380 %, но эти бумаги необходимо очень быстро продать, инвестировав средства в ценные бумаги А.

Доходность такого портфеля будет равна: μр = 4,8 * 0,07 + 3,8 * 0,12 = 0,792 или 79,2 %

Эта доходность будет обеспечена только в случае короткой продажи ценной бумаги Б и дальнейшего нахождения в портфеле только ценной бумаги А.

  1. Определяем риск портфеля максимальной доходности.

Поскольку ценная бумага В обладает максимальной из двух бумаг доходностью, то в случае, если портфель состоит только из бумаг В, он и будет характеризоваться максимальной доходностью.

Риск такого портфеля будет равен: σр2 = ξB, где ξB – риск ценной бумаги В

Отсюда: σр = 0,24 = 4,8 или 480 %



  1. Найти доходность к погашению облигации со сроком обращения 8 лет, номинальной стоимостью 3 000 и купонной ставкой 8%, если: 1) она продаётся за 3 000, 2) её розничная цена увеличится на 10%, 3) уменьшится на 5%.

Решение:

  1. Она продаётся за 3000

3 000 = 240 / R * [1 – 1 / (1 + R)^8] + 3 000 / (1 + R)^8

R = 0,8 или 80%

  1. Её розничная цена увеличится на 10%,

3 000 * 1,1 = 3 300

3 300 = 240 / R * [1 – 1 / (1 + R)^8] + 3 000 / (1 + R)^8

R = 0.0636622 или 6.36%

  1. Уменьшится на 5%

3 000 * 0,95 = 2 850

2 850 = 240 / R * [1 – 1 / (1 + R)^8] + 3 000 / (1 + R)^8

R = 0,089000 или 89%



  1. Портфель состоит из двух ценных бумаг A и B, ожидаемые доходность и риск которых, выраженные в процентах, равны A(14; 27), B(37; 46). Коэффициент корреляции бумаг равен -1, а его доходность равна 20%. Найти портфель и его риск.

Решение:



  1. Текущая цена актива равна 800 USD. Предполагается, что месяц спустяи цена актива может быть равна 770 USD или 840 USD. В рамках однопериодной модели ценообразования опционов вычислить текущую стоимость месячного колл опциона на этот актив, цена исполнения которого равна 820 USD. Процентная ставка постоянна, выполняется непрерывно и равна 7% годовых.

Решение:

  1. S0 = 800 руб.

  2. S0u – цена актива в момент времени t = 1 в случае повышения = 840 руб.

  3. S1(d) = S0d – цена актива в момент времени t = 1 в случае понижения = 760 руб.

  4. Х0 – цена исполнения = 820 руб.

  5. Цена опциона в случае повышения = 840 - 820 = 20 руб.

  6. Стоимость опциона (1 + 0,07/12) * (820 – 800 * (1 + 0,07/12) = 15,42 руб.

Ответ: 15,42 руб.



  1. Текущая цена актива равна 3 000 руб. За год его стоимость может повысится на 18% или понизиться на 15%. Безрисковая годовая ставка равна 10%. Цена исполнения опциона «колл» со сроком исполнения в конце года равна 3 150 руб. Определить величину премии за опцион.

Решение:

  1. Определим величину премии за опцион.

Если цена актива вырастет и составит 1,18 * 3 000 = 3 540 руб., то владелец опциона воспользуется своим правом на покупку актива за 3 000 рублей. Следовательно, цена опциона C1(u) составит 3 540 – 3 150 = 390 руб.

  1. Если цена актива понизится и составит 0,85 * 3 000 = 2 550 руб., то владелец опциона свое право на покупку актива за 3 150 рублей использовать не станет, и цена опциона C1(d) будет равна нулю.



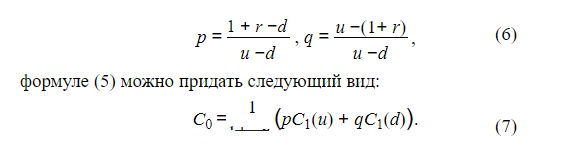
  1. В соответствии с (6) и (7) находим коэффициенты:
    p =



    1,1
    −0,85



    ≈ 0,7575 , q =




    1,2 −1,1



    ≈ 0,2424




    1,18
    −0,85
    1,2 −0,85













  2. Премия за опцион:

Смотрите также файлы