Файл: Задача 122 Исходный опорный план составить методом северозападного угла.docx
Добавлен: 29.10.2023
Просмотров: 96
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача № 122
Исходный опорный план составить методом северо-западного угла.
Найти оптимальный план перевозок, при котором транспортные издержки были бы минимальными.
Из трех пунктов отправления необходимо доставить однородный груз в четыре пункта назначения. Стоимость перевозки единицы груза, его запасы и потребности к ним указаны в табл. 2.
Таблица 2
| Поставщики | Потребители | Запасы | |||
| В1 | В2 | В3 | В4 | ||
| А1 | 6 | 11 | 4 | 10 | 30 |
| А2 | 9 | 8 | 2 | 5 | 60 |
| А3 | 12 | 7 | 1 | 3 | 10 |
| Потребности | 40 | 10 | 20 | 30 | |
Данная задача является задачей транспортного вида (так как суммарный объем производства а аi равен суммарному объему потребления а bi):
а1+а2+а3 =b1+b2+b3+b4
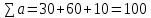
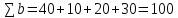
Целевая функция (суммарный пробег порожних вагонов) определяется по формуле:
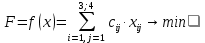
где сij- расстояние перевозки от i-ой станции отправления до j-ой станции назначения; xij - величина перевозки из пункта отправления i-ой станции отправления до j-ой станции назначения.
Система ограничений
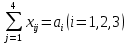
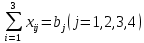
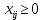
где ai - ресурсы i-ой станции отправления; bj - потребность j-ой станции назначения.
Условие формирования закрытой транспортной задачи:
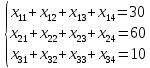
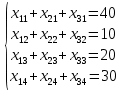
Для решения задачи необходимо построить исходный опорный план перевозок, который в дальнейшем будет подвергаться корректировке.
Построим исходный план методом северо-западного угла.
План начинается заполняться с верхнего левого угла. Значение в клетке (1;1) равно c11=6. Для этого элемента запасы равны 30, потребности 40. Поскольку минимальным является 30, то вычитаем его.
x11 = min(30,40) = 30.
Следующую клетку берем (2;1), значение c21=9. Для этого элемента запасы равны 60, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x21 = min(60,10) = 10.
И так далее получаем опорный план (таблица 3).
Таблица 3 Опорный план методом Северо-Западного угла
| Поставщики | Наличие груза | Потребители | |||
| B1 | B2 | B3 | B4 | ||
| Потребление ресурсов | |||||
| 40 | 10 | 20 | 30 | ||
| A1 | 30 | 6 | 11 | 4 | 10 |
| 30 | | | | ||
| A2 | 60 | 9 | 8 | 2 | 5 |
| 10 | 10 | 20 | 20 | ||
| A3 | 10 | 12 | 7 | 1 | 3 |
| | | | 10 | ||
В результате получен первый опорный план
, который является допустимым, так как все грузы из баз вывезены, потребность потребителей удовлетворена, а план соответствует системе ограничений транспортной задачи.
Число занятых клеток таблицы:
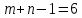
Следовательно, опорный план является невырожденным.
Значение целевой функции для этого опорного плана равно:
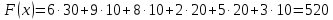
Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых vj - ui = cij, полагая, что u1 = 0.
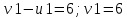
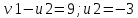
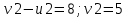
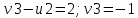
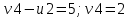
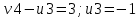
| | v1=6 | v2=5 | v3=-1 | v4=2 |
| u1=0 | 6[30] | 11 | 4 | 10 |
| u2=-3 | 9[10] | 8[10] | 2[20] | 5[20] |
| u3=-1 | 12 | 7 | 1 | 3[10] |
Проверим оценки свободных клеток на соответствие условию vj – ui < cij:
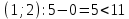
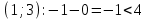
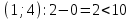
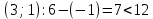
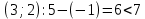
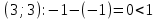
Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию v
j – ui < cij.
Ответ:
От 1-го поставщика необходимо весь груз направить к 1-у потребителю.
От 2-го поставщика необходимо груз направить к 1-у потребителю (10 ед.), к 2-у потребителю (10 ед.), к 3-у потребителю (20 ед.), к 4-у потребителю (20 ед.)
От 3-го поставщика необходимо весь груз направить к 4-у потребителю.
Минимальные затраты составят: