ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 32
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
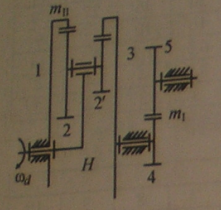
Синтез планетарной передачи:
Дано:
Z4=13
Z5= 26
m1=5
aw=99
i1H3=7
m2=4
Определим число зубьев колёс по формуле:
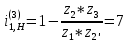
Заменим неизвестные числа зубьев сомножителями:
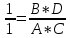
Из условия соосности:
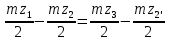
Подставляем и получаем:
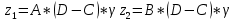
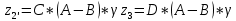,где
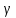– любое целое число.Путём подбора определяем сомножители А, В, С, D:
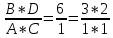
Отсюда: D=2, B=3, C=1, A=1.
Числа зубьев равны
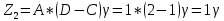
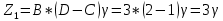
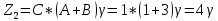
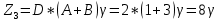
Выбираем значение
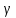, учитывая следующие условия:число зубьев при внешнем зацеплении
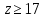;число зубьев при внутреннем зацеплении колеса с внешними зубьями
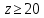.Получаем следующие числа зубьев при
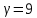для планетарной передачи:z1=18, z2=54, z
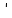2=72, z3=144.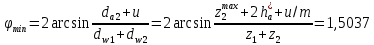
Число сателлитов
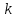будет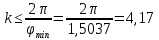 
Для того, чтобы второй сателлит мог быть поставлен на место, которое занимал первый до поворота водила, необходимо чтобы первое колесо повернулось на целое число угловых шагов, что и обеспечивает одинаковое взаимное расположение зубьев центральных колёс z1 и z2, т.е.
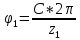
Для того, чтобы установить второй сателлит под углом
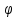к первому, повернём водило на угол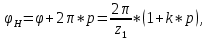 
где
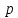- любое целое число.При повороте водила на угол
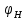первое колесо повернётся на угол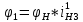
Подставляя (7) и (8) выражения в (9), получаем:
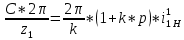
откуда:
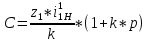. При повороте водила на угол
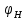первое колесо повернётся на угол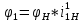
Подставляя (7) и (8) выражения в (9), получаем:
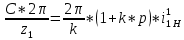
откуда:
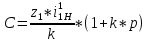. Из полученного следует, что если при каком-либо значении
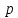возможно получение целого значения C, то сборка механизма возможна.
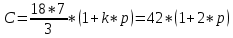.Таким образом, при k=3условие сборки выполняется.
Условие соседства:
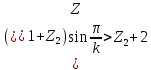
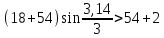
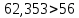
Условие соседства выполняется.
-
Выбираем масштабный коэффициент
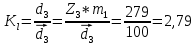
m - модуль зацепления;
z1-число зубьев первого колеса;
d1- длина отрезка, изображающего на плане механизма диаметр первого зубчатого колеса.
-
-
-
-
-
-
-
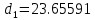
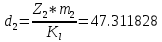
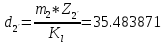
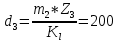
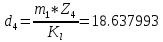
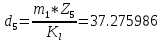
Кинематический анализ механизма графическим методом
Графики линейной скорости
Линия распределения скоростей каждого колеса строится по двум точкам, скорости которых известны. Так для первого звена известны скорость точки B , величина которой задается равным отрезку в 60 мм, и скорость оси вращения колеса равная нулю точка A’. По этим двум точкам строится график распределения окружных скоростей точек водила. Скорость точки C, лежащей на линии касания начальных цилиндров колёс Z1 и Z2 , равна нулю, так как колесо Z1 неподвижно. Проводя прямую через точки B¢¢ и C¢, получим линию 2,2’ , изображающую графики распределения окружных скоростей точек сателлитов Z2 и Z2’ . На этой линии располагается конец отрезка D¢D¢¢ скорости точки D , принадлежащей геометрической оси вращения звеньев Z2 и Z2’, относительно водила. Соединяя точку D¢¢ с точкой A¢ , получаем линию 1,4 графика окружных скоростей планетарного редуктор. На линии 1,4 располагается точка E¢¢ конца отрезка, изображающего окружную скорость точки E , лежащей на линии касания начальных цилиндров зубчатых колес Z4 и Z5. Проводя прямую через точки E¢¢ и F¢ (окружная скорость точки F, лежащей на оси зубчатого колеса Z5 равна нулю) получаем линию 5 графика распределения окружных скоростей точек колеса Z5.
Графики угловой скорости
Построение плана чисел оборотов можно начать с отложения на горизонтальной линии отрезка O1 равного 100 мм. Далее из конца этого отрезка (точка 1) проводим линию параллельную 3 до пересечения ее с вертикальной линией, проведенной из начала отрезка (из точки O). Получим точку пересечения Р, из этой точки проводим линии, параллельные линиям распределения окружных скоростей точек звеньев на графике линейных скоростей.