Файл: Многогранником называется тело, граница которого есть конечное число многоугольников.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 10
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Многогранником называется тело, граница которого есть конечное число многоугольников. Правильным называется многогранник, у которого все грани – правильные равные многоугольники и все двугранные углы равны. Многогранник - правильным, если все его грани – равные правильные многоугольники, а все его вершины одинаково удалены от некоторой точки – центра правильного многоугольника. Многогранник называется n-угольной призмой, если он имеет двумя своими гранями (основаниями) равные n-угольники (не лежащие в одной плоскости), получающиеся друг из друга параллельным переносом, а остальные грани – параллелограммы, противоположными сторонами которых являются соответственные стороны оснований. У прямой призмы боковые грани - прямоугольники. Призма, основание которой параллелограмм, называется параллелепипедом. Пирамидой называется многогранник, который состоит из плоского многоугольника — основания пирамиды, точки, не лежащей в плоскости основания,— вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания Треугольная пирамида называется также тетраэдром. Правильный тетраэдр - все грани правильные треугольники. Усеченной пирамидой называется часть полной пирамиды, заключенная между основанием и параллельным ему сечением. |  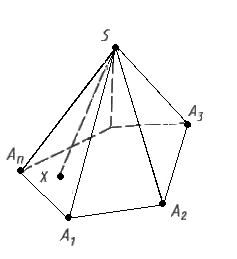 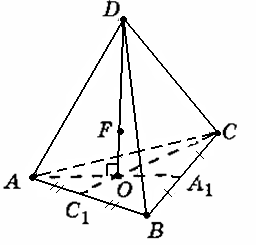 |
| Призма 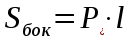 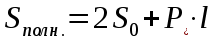 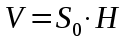 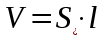 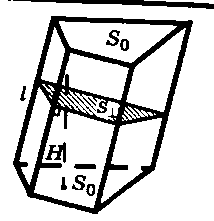 Где Где 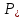 – периметр перпендикулярного сечения, – периметр перпендикулярного сечения, l– длина бокового ребра, 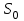 – площадь основания, H– высота призмы, – площадь основания, H– высота призмы, 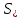 – площадь перпендикулярного сечения. – площадь перпендикулярного сечения. | Пирамида 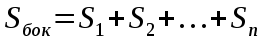 ; ; 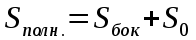 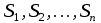 – боковых граней, – боковых граней, 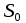 – площадь основ. – площадь основ. Объем пирамиды 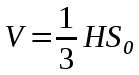 О 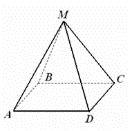 бъем правильной треугольной пирамиды бъем правильной треугольной пирамиды 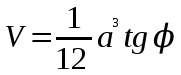 , ребро а, боковые ребра наклонены к пл-ти основ. под углом , ребро а, боковые ребра наклонены к пл-ти основ. под углом |
| п 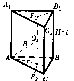 рямой призмы рямой призмы 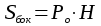 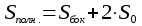 | Объем усеченной пирамиды 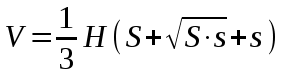 Sиs – площади оснований, Н – высота 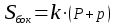 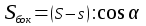  где Р и р - полупериметры оснований, k – апофема, где Р и р - полупериметры оснований, k – апофема, |
| Куб 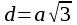 - диагональ куба - диагональ куба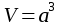 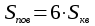 Параллелепипед. Призма, основание которой параллелограмм, называется параллелепипедом. У  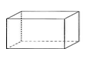 параллелепипеда параллелепипеда 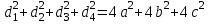 | Тетраэдр Правильный тетраэдр - все грани правильные треугольники. 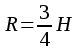 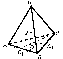 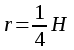 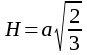 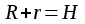 R – радиус описанного шара, r – радиус вписанного шара. R – радиус описанного шара, r – радиус вписанного шара.Площадь поверхности тетраэдра 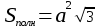 Объем тетраэдра 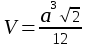 |