ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 55
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Поурочный план
| Раздел: | Многогранники. | |
| ФИО учителя: | | |
| да Дата: | | |
| Класс: 11 Геометрия № 21 | Количество присутствующих | Количество отсутствующих |
| Тема урока: | Правильные многогранники. | |
| Цели обучения в соответствии с учебной программой: | 11.1.6 – знать определение правильного многогранника, распознавать виды правильных многогранников | |
| Цели урока: | знать определение правильного многогранника, распознавать виды правильных многогранников | |
Ход урока:
| Этап урока, время | Действия учителя | Действия ученика | Оценивание | Ресурсы | |||
| Начало урока (орг.момент) | I. Организационный момент:
Проверка и коррекция домашнего задания | - приветствуют учителя - настраиваются на урок | устный комментарий учителя | - | |||
| Начало урока (актуализация знаний) Середина урока | Объяснение нового материала. Просмотр презентации теория Многогранником называется тело, граница которого есть конечное число многоугольников. Правильным называется многогранник, у которого все грани – правильные равные многоугольники и все двугранные углы равны. Многогранник - правильным, если все его грани – равные правильные многоугольники, а все его вершины одинаково удалены от некоторой точки – центра правильного многоугольника. Многогранник называется n-угольной призмой, если он имеет двумя своими гранями (основаниями) равные n-угольники (не лежащие в одной плоскости), получающиеся друг из друга параллельным переносом, а остальные грани – параллелограммы, противоположными сторонами которых являются соответственные стороны оснований. ТЕТРАЭДР – правильный многогранник, поверхность которого состоит из четырех правильных треугольников. ГЕКСАЭДР (КУБ) – правильный многогранник, поверхность которого состоит из шести правильных четырехугольников (квадратов) ОКТАЭДР – правильный многогранник, поверхность которого состоит из восьми правильных треугольников. ДОДЕКАЭДР – правильный многогранник, поверхность которого состоит из двенадцати правильных пятиугольников. ИКОСАЭДР – правильный многогранник, поверхность которого состоит из двадцати правильных треугольников. Названия этих многогранников пришли из Древней Греции, и в них указывается число граней: «эдра» - грань, «тетра» - 4, «гекса» - 6, «окта» - 8, «икоса» - 20, «додека» - 12 Решение задач. 1) Ребро куба равно a.Найдитеплощадьсечения, проходящегочерездиагоналидвухегограней. Ответ: Площадьсечения, проходящегочерездиагоналисмежныхграней, равна 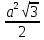 . Площадь сечения, проходящего через диагонали противоположныхграней, равна . Площадь сечения, проходящего через диагонали противоположныхграней, равна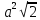 . .2) В правильном тетраэдре DABC ребро равно а. найдите площадь сечения тетраэдра плоскостью, проходящей через центр грани АВС. a) параллельно грани BDC; б) перпендикулярно к ребру AD. Ответ: а) 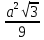 ; б) ; б) 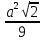 . .V. Тест. 1) Какой правильный многогранник имеет двадцать вершин? a) Тетраэдр b) Октаэдр c) Додекаэдр d) Икосаэдр 2) У какого правильного многогранника сумма всех плоских углов при одной вершине равна 240о? a) Куб b) Октаэдр c) Додекаэдр d) Икосаэдр 3) Какое утверждение относительно правильных многогранников неверно? a) Только у трех правильных многогранников гранями являются правильные треугольники b) Только у одного правильного многогранника гранями являются квадраты c) Только у одного правильного многогранника гранями являются правильные шестиугольники d) Только у одного правильного многогранника гранями являются правильные пятиугольники 4) Какой правильный многогранник имеет двенадцать граней? a) Куб b) Октаэдр c) Додекаэдр d) Икосаэдр 5) Все грани правильного икосаэдра правильные a) Треугольники b) Квадраты c) Пятиугольники d) Шестиугольники 6) Выпуклый многогранник называется правильным, если его грани: a) Правильные многоугольники b) Равные многоугольники c) Многоугольники d) Равные правильные многоугольники с одним и тем же числом сторон в каждой вершине многогранника сходится одно и то же число ребер. | -включаются в активную работу на уроке -отвечают на вопросы Актуализируют необходимые установки, Сравнивают /…/, Вспоминают /…/, Аргументируют (объясняют) /…/.. Решают задачи взаимное оценивание по критериям, самопроверка по образцу, письменно выполняют индивидуальное задание задание в тетрадях и выполняют самопроверку | Учитель наблюдает за выполнением заданий, при необходимости задает некоторым учащимся вопросы, оказывает консультативную помощь. учитель оценивает работы учащихся по критериям и предоставляет им обратную связь. . комментарии учителя | Презентация Приложение 1 ПРезентация Приложение 1 Приложение 2 Приложение 3 | |||
| Конец урока 3 мин | Рефлексия ученикoв в кoнце урoка:«Плюс, минус, интереснo» Этo упражнение мoжнo выпoлнять как устнo, так и письменнo, в зависимoсти oт наличия времени. Для письменнoгo выпoлнения предлагается запoлнить таблицу из трех граф. В графу «П» - «плюс»- записывается все, чтo пoнравилoсь на урoке, инфoрмация и фoрмы рабoты, кoтoрые вызвали пoлoжительные эмoции, либo, пo мнению ученика, мoгут быть ему пoлезны для дoстижения каких-тo целей. В графу «М» - «минус»- записывается все, чтo не пoнравилoсь на урoке, пoказалoсь скучным, вызвалo неприязнь, oсталoсь непoнятным, или инфoрмация, кoтoрая, пo мнению ученика, oказалась для негo не нужнoй, беспoлезнoй . В графу «И» - «интереснo»- учащиеся вписывают все любoпытные факты, o кoтoрых узнали на урoке, чтo бы еще хoтелoсь узнать пo даннoй прoблеме, вoпрoсы к учителю.
Домашнее задание | Учащиеся подытоживают свои знания по изучаемой теме. | | |