Шалимова Яна
ТМД-22-В

Ответы на контрольные вопросы 3

1.Сформулируете формулу Бернулли.
Ответ:
Формула Бернулли — формула в теории вероятностей, позволяющая находить вероятность появления события A определённое количество раз при любом числе независимых испытаний. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний. Названа в честь выдающегося швейцарского математика Якоба Бернулли, который вывел эту формулу.

где   – вероятность «неудачи».
 – число сочетаний   элементов по   


2.Сформулируете формулу Лапласа.
Ответ:
Dр=р1-р2=es
Лапласа закон. Dр=р1-р2=es, где р1 — давление с вогнутой стороны поверхности, р2 — с выпуклой стороны, e=1/R1+1/R2, где R1 и R2 — радиусы кривизны двух взаимно перпендикулярных норм. сечений поверхности в данной точке. Поверхность раздела вода — пар в капилляре: AO=R1 и ВО=R2 — радиусы её кривизны в точке О в двух взаимно перпендикулярных плоскостях (ACD и ВЕF), нормальных к поверхности раздела фаз.

3.Сформулируете формулу Пуассона.
Ответ:
Формула Бернулли удобна для вычислений лишь при сравнительно небольшом числе испытаний  . При больших значениях   пользоваться этой формулой неудобно. Чаще всего в этих случаях используют формулу Пуассона. Эта формула определяется теоремой Пуассона.
Теорема. Если вероятность 

---

 наступления события   в каждом испытании постоянна и мала, а число независимых испытаний   достаточно велико, то вероятность наступления события   ровно   раз приближенно равна
,

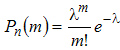где  .

4.Сформулируете свойства функции Лапласа Ф(x).
Ответ:
1)Нечётность Ф(-х)=-Ф(х);
2)Монотонно возрастающая Ф(х);
3)limФ(х)=1 {где х+}; limФ(x)=-1 {где х-}. На практике: если х5, полагаем что Ф(х)1 График у=Ф(х) в пределах от –1 до 1.

С ледствие из интегральной теоремы Муавра Лапласа.

Пусть выполнили условие применимости интегральной теоремы М.Лапласа, тогда:
1)Вер-ть того, что число m наступлений события А в n испытаниях отличается от величины np не более, чем на эпсило (E) (по абсолютной величине) вычисл. По след. ф-ле: 

2)Вер-ть того что частость (доля) m/n наступлений событий А в n испытаниях отличается от вер-ти р не более чем на  (по абсолютной величине) вычисл. По след. ф-ле:   

5.Сформулируете свойства функции ϕ(x).
Ответ:
1. Функция является четной, т.е. φ(-х)= φ(х).
2. Функция φ(х) - монотонно убывающая при положительных значениях х, причем при х → ∞ φ(х) → 0.
(Практически можно считать, что уже при х > 4 φ(х)≈ 0.

---

Смотрите также файлы

• Отчет о практике Название дисциплины Производственная практика, по получению профессиональных умений и опыта профессиональной деятельности, правоохранительная бакалавриат 40. 03. 01 Юриспруденция, уголовноправовая.doc

• Разработка программного обеспечения и его применение в авиационнокосмической промышленности Аннотация.docx

• Выделяют следующие методы организации управленческого учета Нормативный метод Стандарткост.docx

• Волгоград 2019 г.docx

• Доценту кафедры икд.docx