Файл: Данилочев Д. В., Глинский И. В., Карымсакова Л. И. Способ повышения достоверности входных сообщений в асу на основе многоальтернативного сличения.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 15
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Данилочев Д.В., Глинский И.В., Карымсакова Л.И.
СПОСОБ ПОВЫШЕНИЯ ДОСТОВЕРНОСТИ ВХОДНЫХ СООБЩЕНИЙ В АСУ НА ОСНОВЕ МНОГОАЛЬТЕРНАТИВНОГО СЛИЧЕНИЯ
Аннотация. В данной статье рассмотрен способ распознавания сложных сигналов в условиях мешающих воздействий. Используемый математический аппарат основан на методе оптимального поиска Эгервари («венгерский метод»). В статье подробно расписана реализация отождествления нескольких сигналов по имеющимся параметрам, получаемым на входе приемного тракта.Данный метод позволяет производить определение соответствия принимаемых сигналов расчетным.
Annotation. This article discusses how the recognition of complex signals in conditions of interference effects. The mathematical apparatus used is based on the Egervari optimal search method ("Hungarian method"). The article describes in detail the implementation of identification of several signals based on the available parameters received at the input of the receiving path. This method allows you to determine whether the received signals correspond to the calculated ones.
Ключевые слова. Сложные сигналы, сличение, метод Эгервари, экстраполяционный сигнал.
Key words. Complex signals, comparison, Egervari method, extrapolation signal.
Современные системы обработки информации специального назначения в процессе функционирования сталкиваются с задачей обнаружения и распознавания поступающих на приемные устройства зашумленных сигналов. В зависимости от помеховой обстановки вероятность правильного распознавания получаемых сигналов и команд может меняться от приемлемой до неудовлетворительной. В связи с этим, для решения данной задачи была рассмотрена возможность использования алгоритмов сличения.
В практически реализуемых алгоритмах сличения радиосигналов в процессе отождествления и идентификации рассчитываются стробы возможных отклонений параметров сигнала, таких как частота, ожидаемая мощность, форма спектра и т.д., которые в последствии могут перекрывать друг друга. Для определения принадлежности данных наборов параметров к тому или иному сигналу необходимо рассчитать объединенную область (объединенный строб), включающую исходные стробы.
Считается, что координатные точки, находящиеся в выделенной области, могут принадлежать к любому из попавших в полосу пропускания принятых сигналов. При наличии двух сигналов и двух наборов параметров возможны две комбинации сличения; при трех наборах число комбинаций увеличивается до шести; в общем случае при
N сигналов и N наборов возможно N-факториал (Ni) комбинаций сличения [1].
В реальной обстановке объединенный строб может включать порядка 10 и даже более пар принятых сигналов (ПС) и экстраполяционных сигналов (ЭС). В таком случае, необходимо проанализировать более трех миллионов (10!=3628800) комбинаций сличения ПСi и ЭСi. При этом для каждой комбинации следует рассчитать сумму квадратов расстояния между сличаемыми ПС и ЭС, а далее выбрать комбинацию сличения, для которой указанная сумма является минимальной.
Очевидно, что операция сличения в предложенном варианте ее выполнения связана с существенными затратами вычислительных средств. В этой связи представляют интерес методы математического программирования, которые позволяют находить минимум линейных функций конечного числа переменных [2]. Использование методов линейного программирования применительно к многоальтернативному сличению предусматривает следующие предварительные операции:
1. Определение исходных данных, в качестве которых используются параметры ПС и ЭС, находящихся в области объединенного строба.
2. Составление матрицы L, элементами которой являются квадраты расстояний между анализируемыми ПС и ЭС:
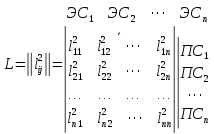
Выделим систему nнезависимых элементов
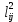, сумма которых является минимальной. Таким образом индексы ij найденных элементов 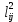представляют наилучший, согласно критерию наименьших квадратов, вариант сличения совокупности ПС и ЭС.Наиболее эффективным, позволяющим выделить минимизирующий выбор из матрицы является «венгерский» метод, предложенный математиком Эгервари [3]. Путем эквивалентных логических преобразований матрицы L данный метод позволяет быстро определить элементы матрицы, которым соответствует оптимальный вариант сличения.
Имеется выборка сигнала точек портрета и точек, полученных при сканировании объекта (рис. 1).
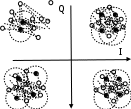
Рис.1 – Сличение точек сигнала
Составим матрицу, элементами которой являются квадраты расстояний между
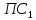
и
:
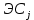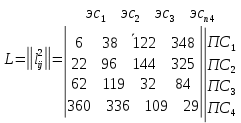
Вычтем из элементов каждого столбца его наименьший элемент (наименьшие элементы столбцов - 6; 38; 32; 29) и заменим все элементы матрицы полученными разностями:
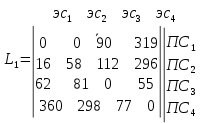
Вычтем наименьший элемент каждой строки из всех элементов данной строки. В примере наименьшими элементами строк являются 0, 16, 0, 0, а значит матрица
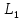заменяется на 
.
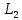Определим систему независимых нулей, т.е. выделим звездочкой какой-либо нуль первого столбца, затем независимый от первого нуль второго столбца (т.е. нуль не в строке с выделенным ранее):
Если число независимых нулей равно четырем (для общего случая - равно n), то места (ij) независимых нулей определяют оптимальный выбор :i-я ЭС сличается с j-й
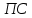. В рассматриваемом примере число независимых нулей равно трем, и поэтому задачу выбора следует продолжить. Выделим знаком «+» столбцы, содержащие нули со звездочкой :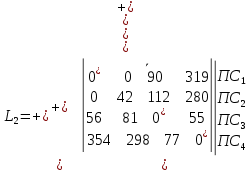
Найдем невыделенный нуль. Таковыми являются элемент, индексы которого ij=12. Пометим данный нуль штрихом, т.е.
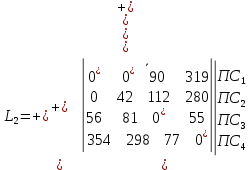
В первой строке имеется
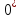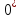и . Выделим данную строку знаком «+» и одновременно уничтожим знак «+» над столбцом с 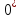. Найдем следующий невыделенный нуль (ij=21) и повторим операцию:
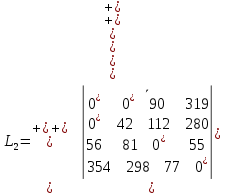
Выделим цепочку от найденного
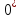
(в одной строке, с которым нет
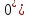по столбцу к 
, от к , т.е.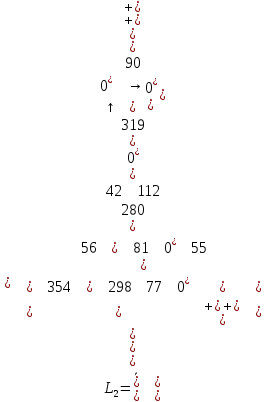
Уничтожим в цепочке звездочку и поставим звездочки вместо штрихов:
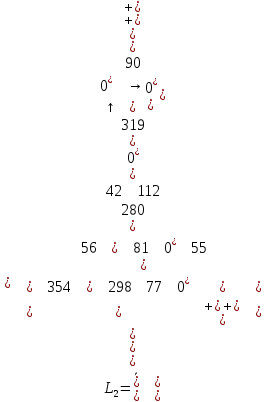
Поскольку число независимых нулей равно четырем (имеется четыре символа «+»), то задача оптимизации выбора считается завершенной. Результатом ее решения является выбор элементов первоначальной матрицы L на местах независимых нулей (
) преобразованной матрицы 
. В рассматриваемой постановке задачи главное не выбор элементов, а выявление индексов системы независимых нулей, которые определяют пары сличенных ПС и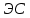 
:
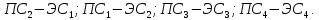
При проверке аналогии видно, что любой иной вариант сличения приводит к увеличению суммы квадратов расстояний между соответствующими парами
и 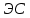.Литература
-
Злобин В.И. Метод абдукции и проблемы логики научных исследований. - М.: МО РФ, 1996. - 278 с.
2. Злобин В.И., Данилюк С.Г. Математическое и техническое обеспечение. Основы обработки радиолокационной информации. – СпБ.: Издание СПВВУРЭ, 2002. – 192 с.
3. Виноградов А.П. Основы обработки радиолокационной информации. ФВУ ПВО, СпБ., 2002 г., стр.190
4. Томаси У. Электронные системы связи. – М.:Техносфера, 2007.-1360 с.
5. Шумоподобные сигналы в системах передачи информации/ В.Пестряков, В.Афанасьев, В. Гурвиц – М.: «Сов.Радио», 1973. – 424 с.
Филатов Владимир Иванович - к.т.н., доцент ВА РВСН им. Петра Великого; Московская область, г. Балашиха 8(977)678-01-69;
Бударин Денис Владимирович – младший научный сотрудник ВА РВСН им. Петра Великого, Московская область, г.Балашиха, d.budarin@mail.ru;
Попов Александр Михайлович – действительный член Академии военных наук, д-р тех. наук, профессор, советник директора по науке, Институт машиноведения им. А
.А. БлагонравоваРАН, г. Москва, 8 (916)333-66-12, aproximandra@mail.ru.
Filatov Vladimir Ivanovich is a PhD in Technological Sciences, the associate professor of VA RVSN of Peter the Great; Moscow region, Balashikha 8(977)678-01-69;
Budarin Denis Vladimirovich is the junior researcher of VA RVSN of Peter the Great, the Moscow region, Balashikha, d.budarin@mail.ru;
Popov Alexander Mikhaylovich is a full member of Academy of military sciences, the Dr. of technical sciences, professor, the adviser to the director of science, Institute of engineering science of A.A. Blagonravov of RAS, Moscow, 8 (916)333-66-12, aproximandra@mail.ru.