Добавлен: 30.10.2023
Просмотров: 168
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное государственное бюджетное учреждения высшего профессионального образования <<Санкт-Петербургский государственный морской технический университет >>
Кафедра Судовой автоматики и измерений
Курсовая работа
по дисциплине <<Теория автоматического регулирования>>
На тему «Система автоматического регулирования»
Выполнил:
студент гр. 2295
Бундюк Ю.В.
Руководитель:
к. э. н., доц.
Согонов С. А
г. Санкт-Петербург, 2023 г.
Тип автоматической системы САР:
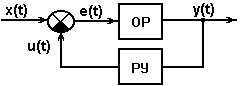 | ||||||||||
| | | | В структурных схемах обозначены: | | | |||||
| ОР | - | объект регулирования; | РУ | - | регулирующее устройство; | |||||
| e(t) | - | величина рассогласования; | x(t) | - | задающее воздействие (входная величина); | |||||
| u(t) | - | управляющее воздействие; | y(t) | - | управляемая величина (выходная переменная); | |||||
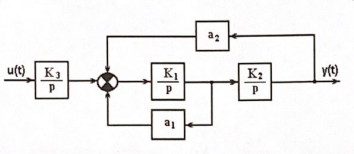
Типы структурных схем ОР:
 |
Типы структурных схем РУ:
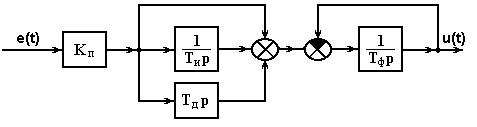 Коэффициенты ОР(ИУ) К1 = 1,8 К2 = 2,1 К3 = 1,15 а1 = 2 а2 = 2,5 Коэффициенты РУ(УУ) Кп = 10 Ти = 325 Тд = 65 Тф = 8 |
Рассмотрим ОР:
Из условия:
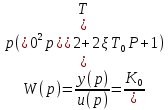
Из структурной схемы:
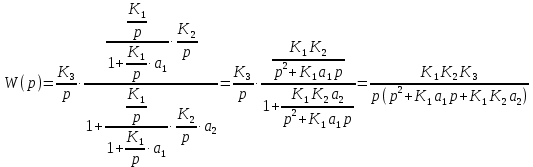
Чтобы получить искомые коэффициенты, приравняем эти 2 функции и подставим коэффициенты из условия:
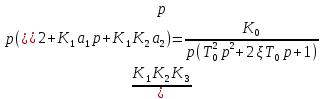
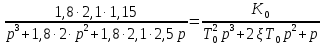
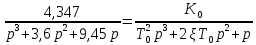
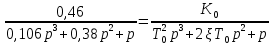
Получаем:
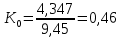
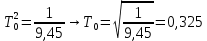
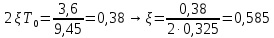
Рассмотрим РУ:
Передаточная функция по структурной схеме:
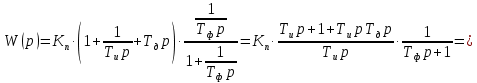
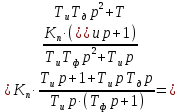
Вид передаточной функции по условию задачи:
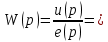
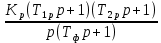
Поступаем аналогично
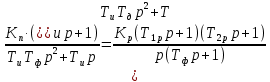
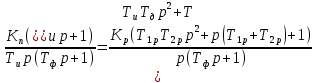
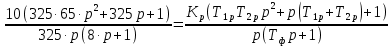
Получаем:
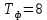
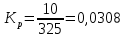
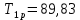
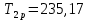
Исследование объекта регулирования
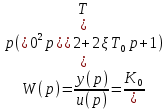
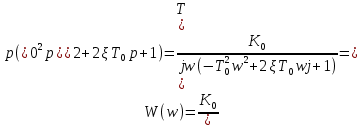
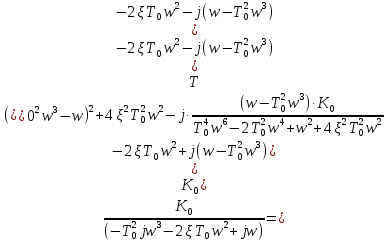
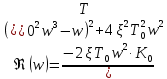
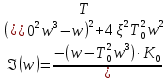
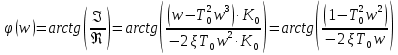
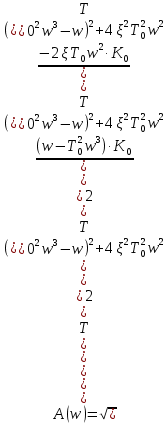
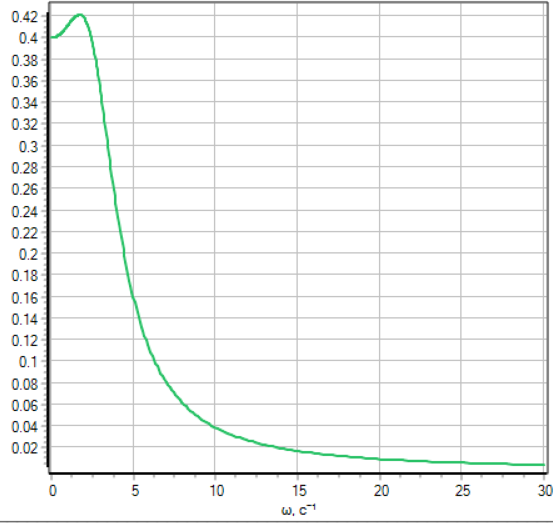
АЧХ
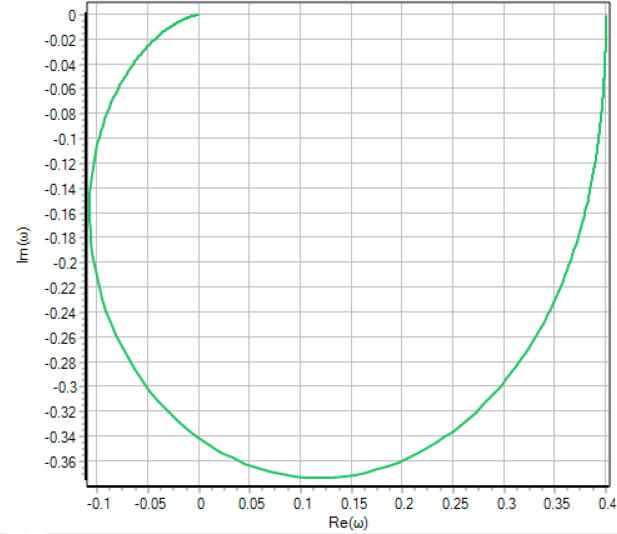
АФЧХ
ФЧХ
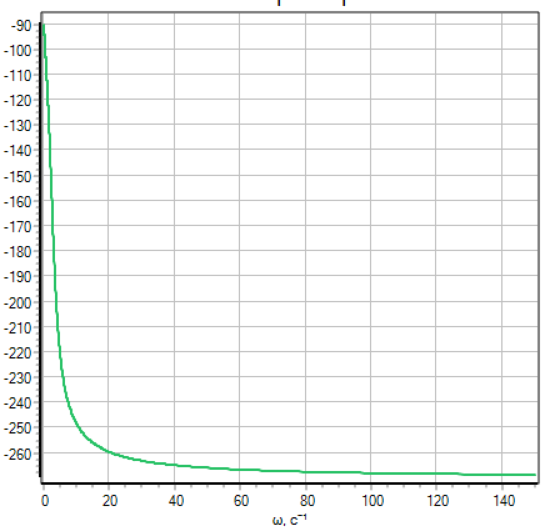
ЛАЧХ
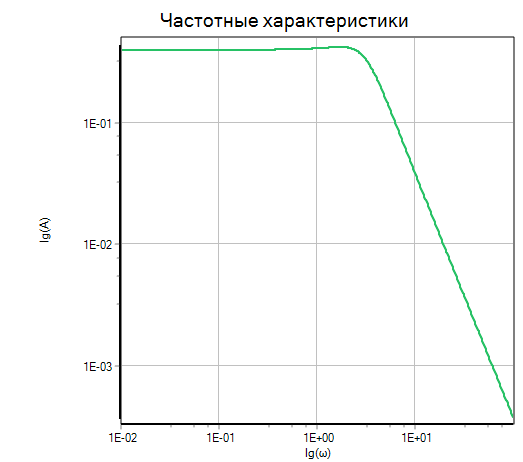
ЛФЧХ
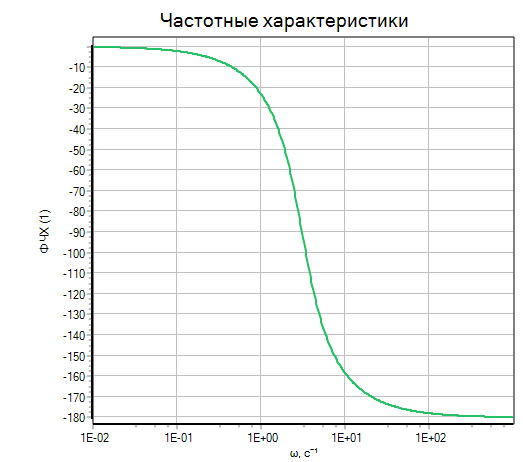
ЛАФЧХ
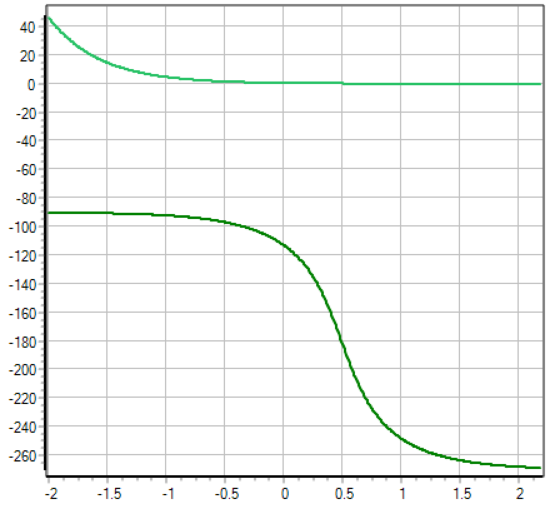
Исследование регулирующего устройства
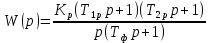
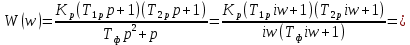
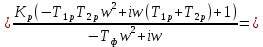
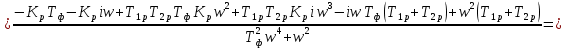
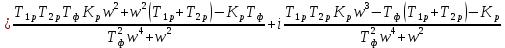
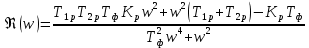
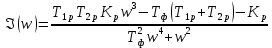
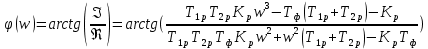
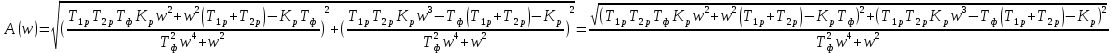
АЧХ
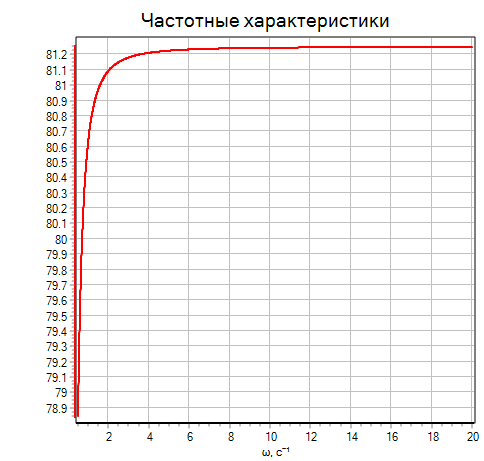
АФЧХ
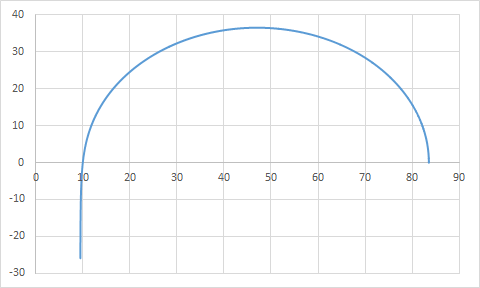
ФЧХ
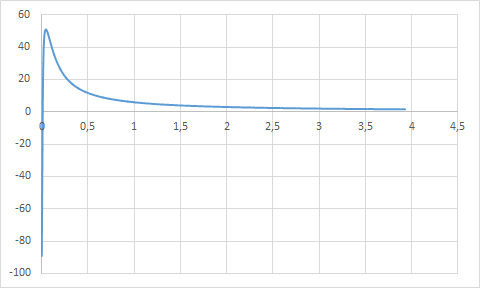
ЛФЧХ
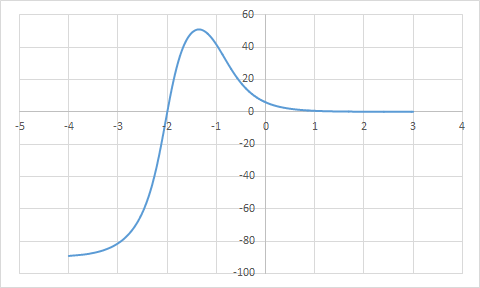
ЛАЧХ
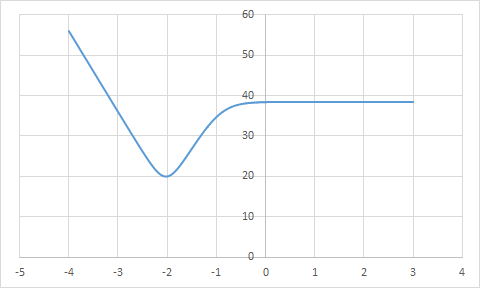
Исследование разомкнутой системы
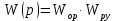
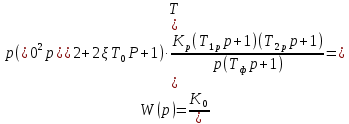
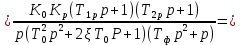
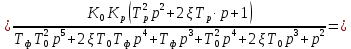
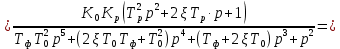
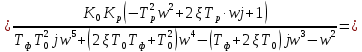
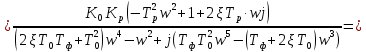
Пусть
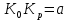
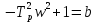
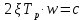
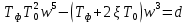
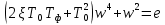
Тогда
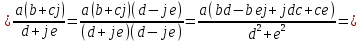
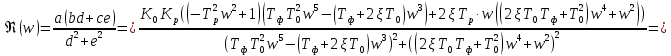
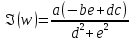
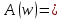
АЧХ
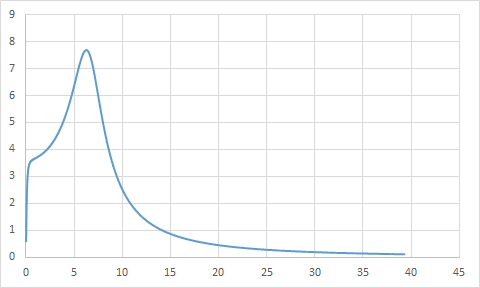
АФЧХ
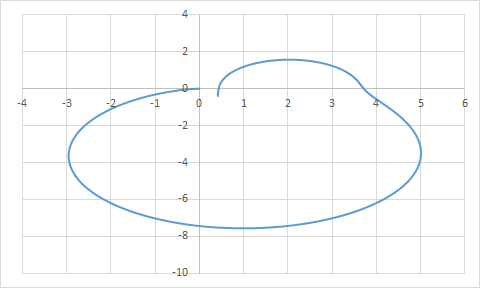
ФЧХ
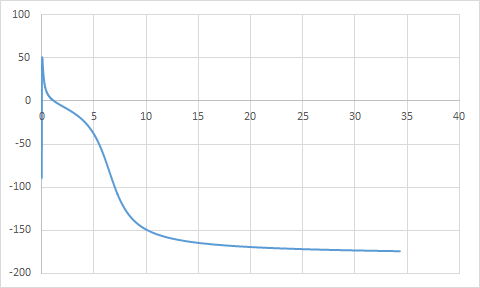
ЛФЧХ
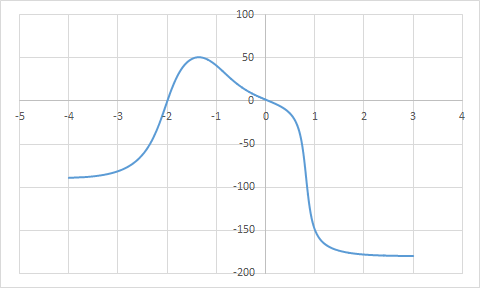
ЛАЧХ
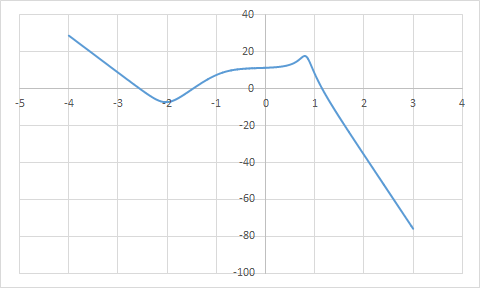
Определение устойчивости заданной системы
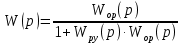
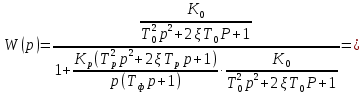
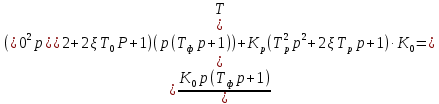
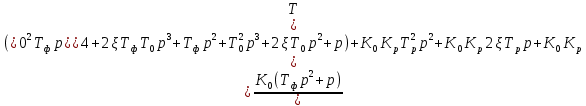
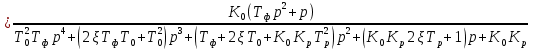
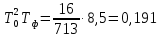
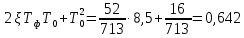
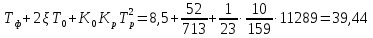
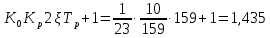
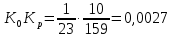
Таким образом, характеристический полином имеет вид:
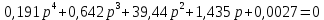
Рассмотрим корневой критерий устойчивости:
Найдём корни из характеристического полинома:
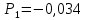
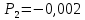
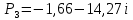
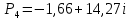
Система устойчива, т.к. все корни лежат в левой полуплоскости.
Рассмотрим критерий устойчивости Рауса-Гурвица.
Для определения устойчивости системы составим матрицу Гурвица, учитывая коэффициенты характеристического полином.
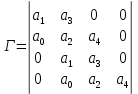
Из данной матрицы имеем диагональные миноры:
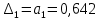
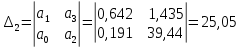
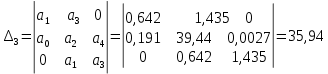
Можно сделать вывод, что система устойчива, т.к. диагональные миноры больше нуля.
Рассмотрим критерий устойчивости Липатова-Соколова
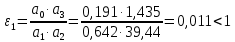
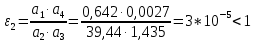
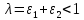
Делаем вывод, что система устойчива, т.к. удовлетворяет неравенству.
Рассмотрим критерий устойчивости Михайлова
Выполним замену в характеристическом полиноме p=i∙w

Получим:
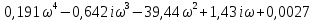 = 0
= 0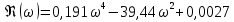
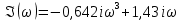
Построим по данным уравнения годограф
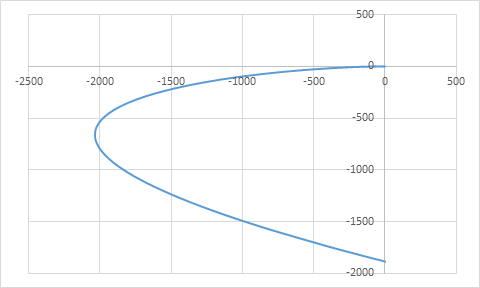
В приближении
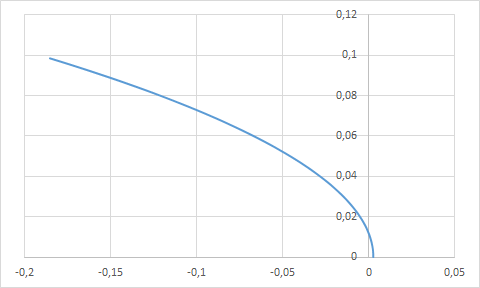
График охватывает начало координат, имеет спиралевидную форму и последовательно обходит квадранты, следовательно - система устойчива
Рассмотрим критерий устойчивости Найквиста
Обратимся к АФЧХ разомкнутой системы

График не огибает точку (-1,i0), а это значит, что система является устойчивой
Рассмотрим логарифмический критерий устойчивости Найквиста
Замкнутая система будет устойчива, если ЛАЧХ разомкнутой системы пересекает ось абсцисс раньше, чем ЛФЧХ достигает значение -180°
ЛФЧХ

ЛАЧХ

Из графиков очевидно, что ЛАЧХ пересекает ось абсцисс раньше, чем ЛФЧХ достигает -180°, следовательно, система устойчива
График переходного процесса
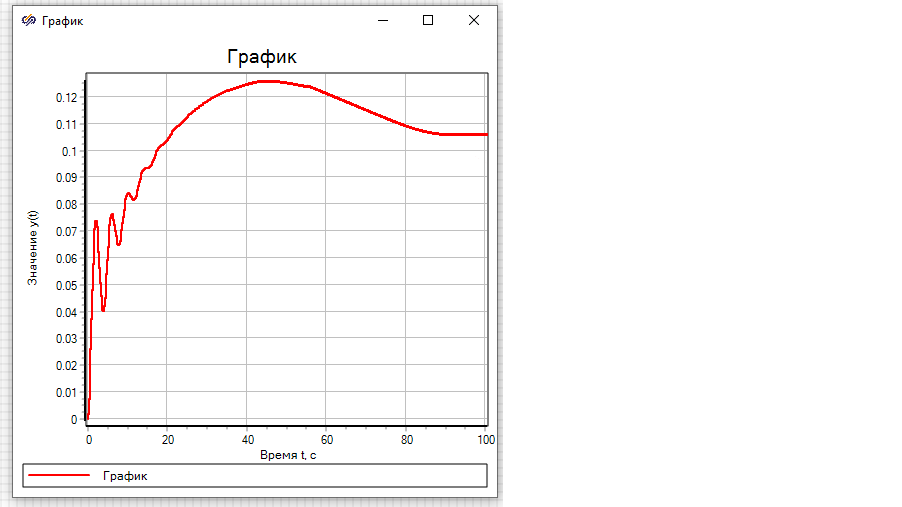
Изменим коэффициенты регулятора