Добавлен: 30.10.2023
Просмотров: 171
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, чтобы сделать систему более качественной
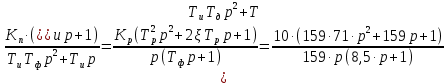
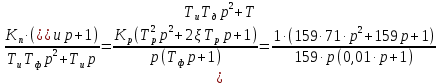
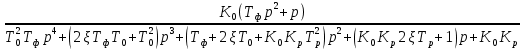
Таким образом, характеристический полином имеет вид:
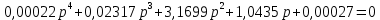
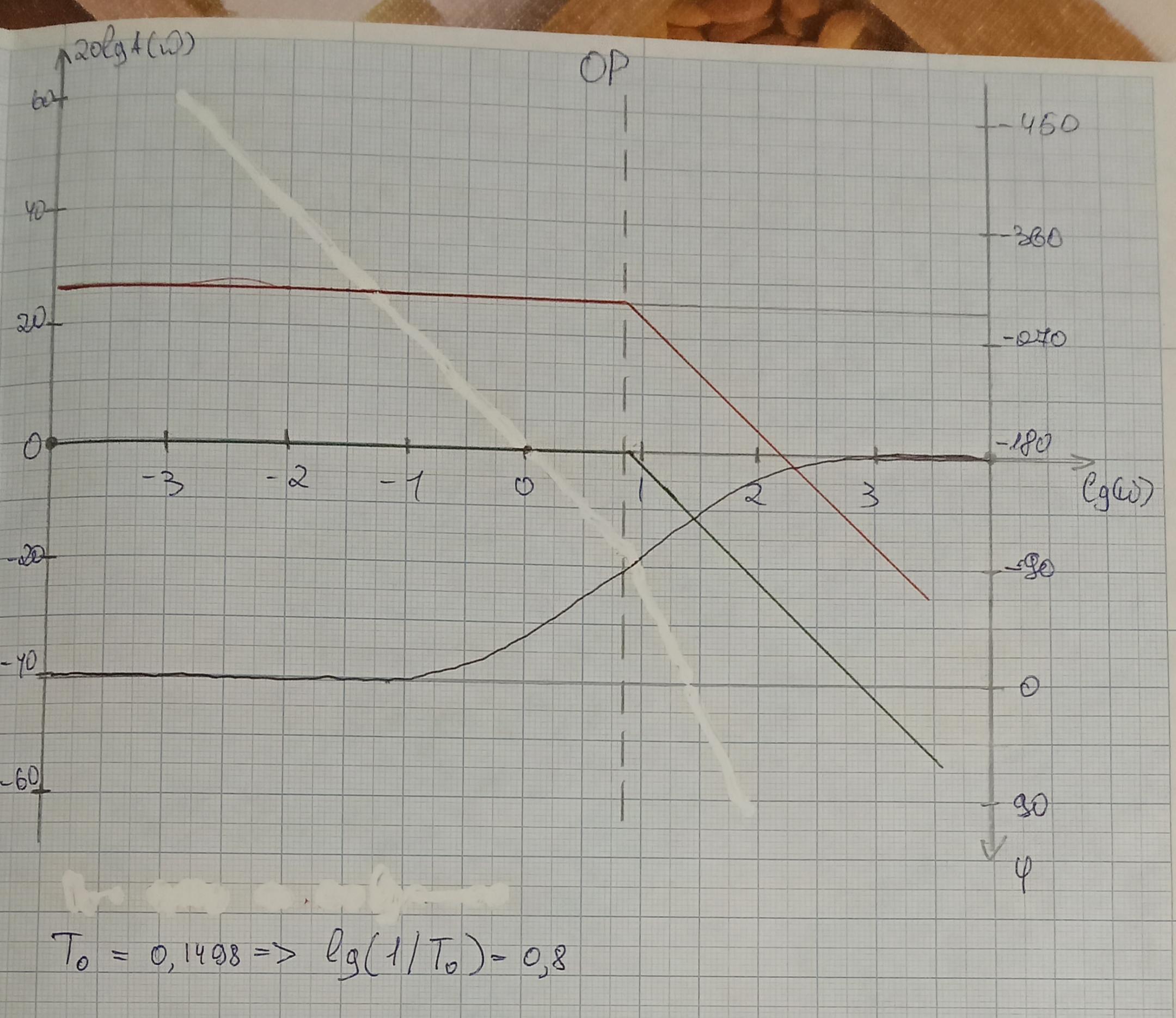
График переходного процесса
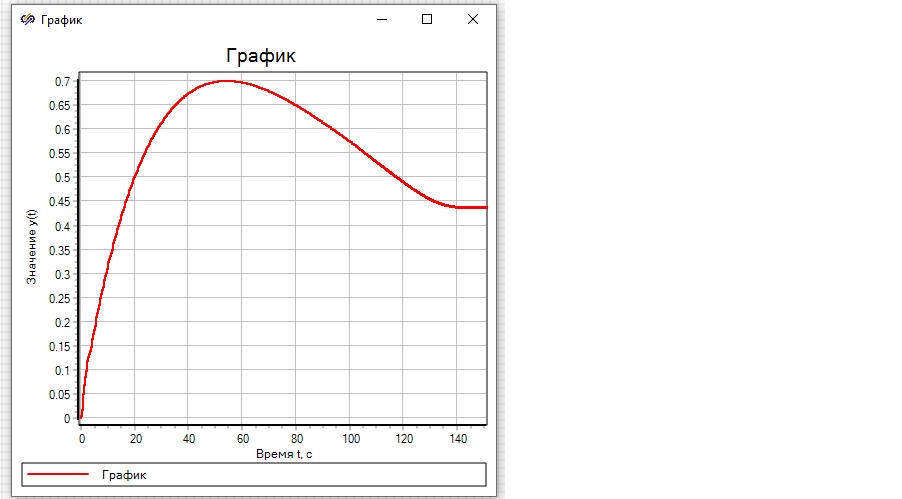
Система стала более качественной, так как перерегулирование практически отсутствует
Т.к. количество колебаний не превышает трёх – система качественна.
Рассмотрим критерий устойчивости Рауса-Гурвица.
Для определения устойчивости системы составим матрицу Гурвица, учитывая коэффициенты характеристического полином.
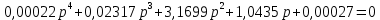
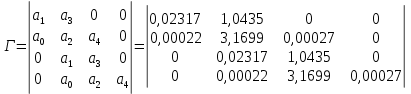
Из данной матрицы имеем диагональные миноры:
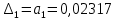
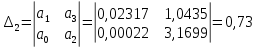
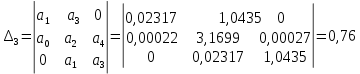
Можно сделать вывод, что система устойчива, т.к. диагональные миноры больше нуля.
Рассмотрим критерий устойчивости Липатова-Соколова
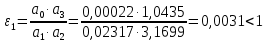
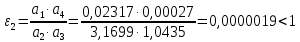
Делаем вывод, что
система устойчива, т.к. удовлетворяет неравенству.
Рассмотрим критерий устойчивости Михайлова
Выполним замену в характеристическом полиноме p=i∙w
Получим:
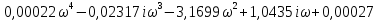= 0
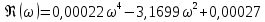
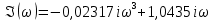
Так как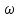
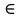[0;+∞), отрицательные значения рассматривать не будем.
Составим таблицу значений:
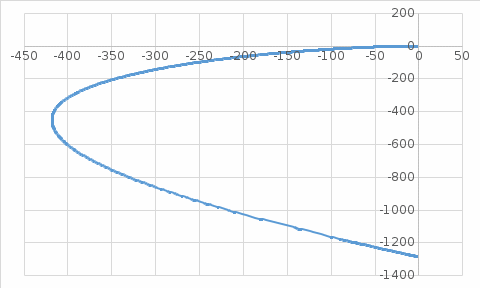
В приближении
-0,004 -0,003 -0,002 -0,001 0 0,001
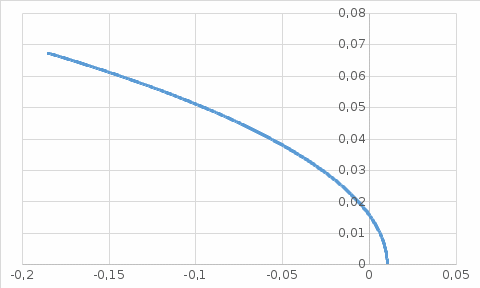
Годограф обходит квадранты последовательно, имеет спиралевидной форму, следовательно - система устойчива
Быстродействие системы определяется степенью устойчивости η – так называется расстояние мнимой оси до ближайшего корня (или пары комплексно-сопряженных корней).
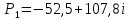
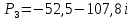
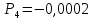
Система устойчива, т.к. действительные части комплексных корней лежат в левой полуплоскости
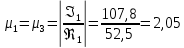
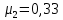
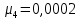
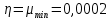
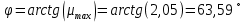
Запас устойчивости
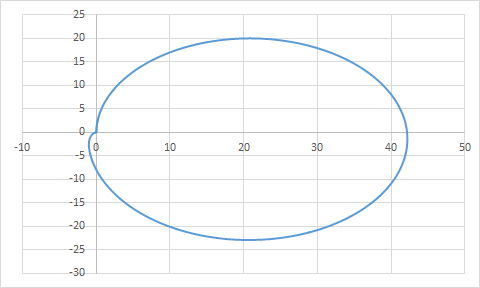
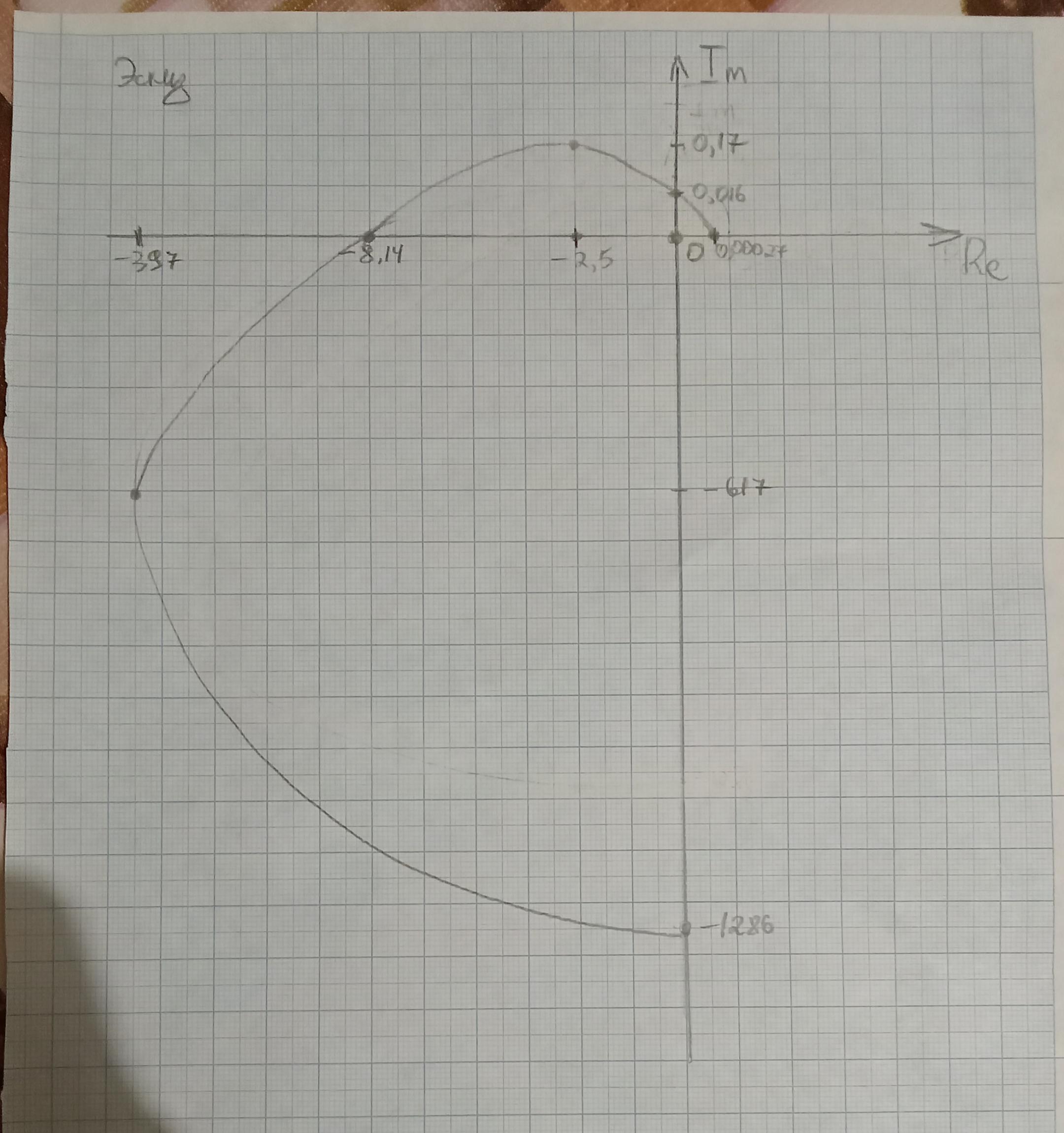
Обратимся к годографу Найквиста (АФЧХ замкнутой системы)
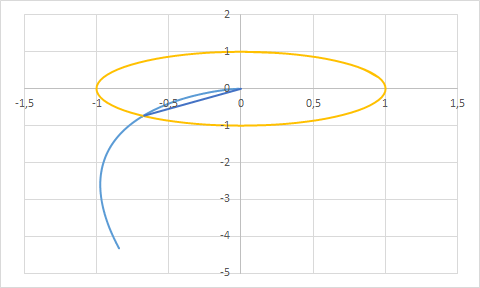
Запас по фазе: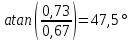
Для определения запаса по амплитуде необходимо найти расстояние от (-1;0) до точки пересечения с этой же полуосью
В практических задачах нужно обеспечивать запас по амплитуде не менее 6 дБ
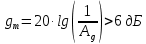
Чтобы выполнялось данное условие, необходимо, чтобы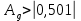
Для нашего случая – это условие выполняется
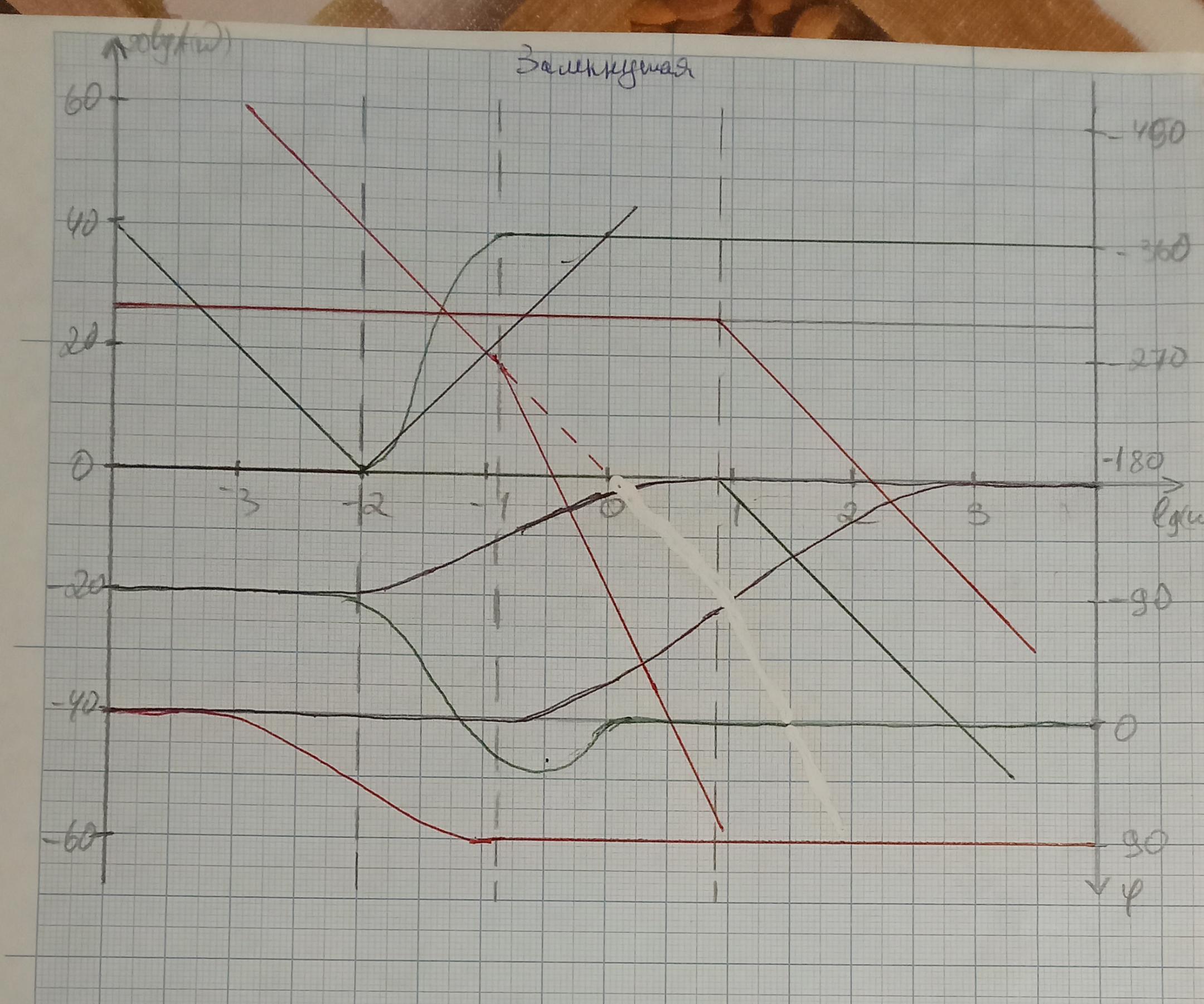
Запасы устойчивости по ЛАФЧХ
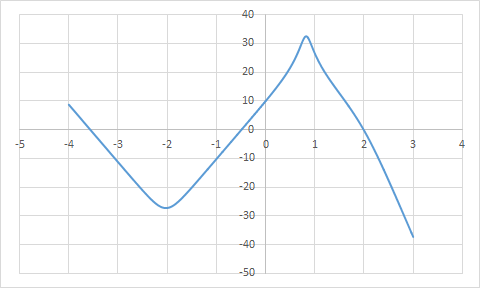
ЛФЧХ
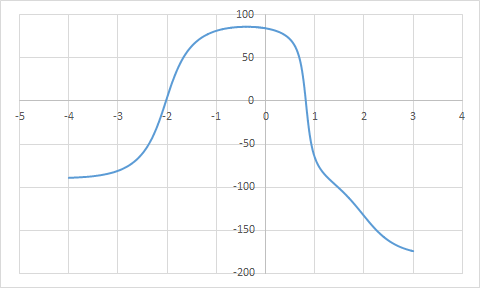
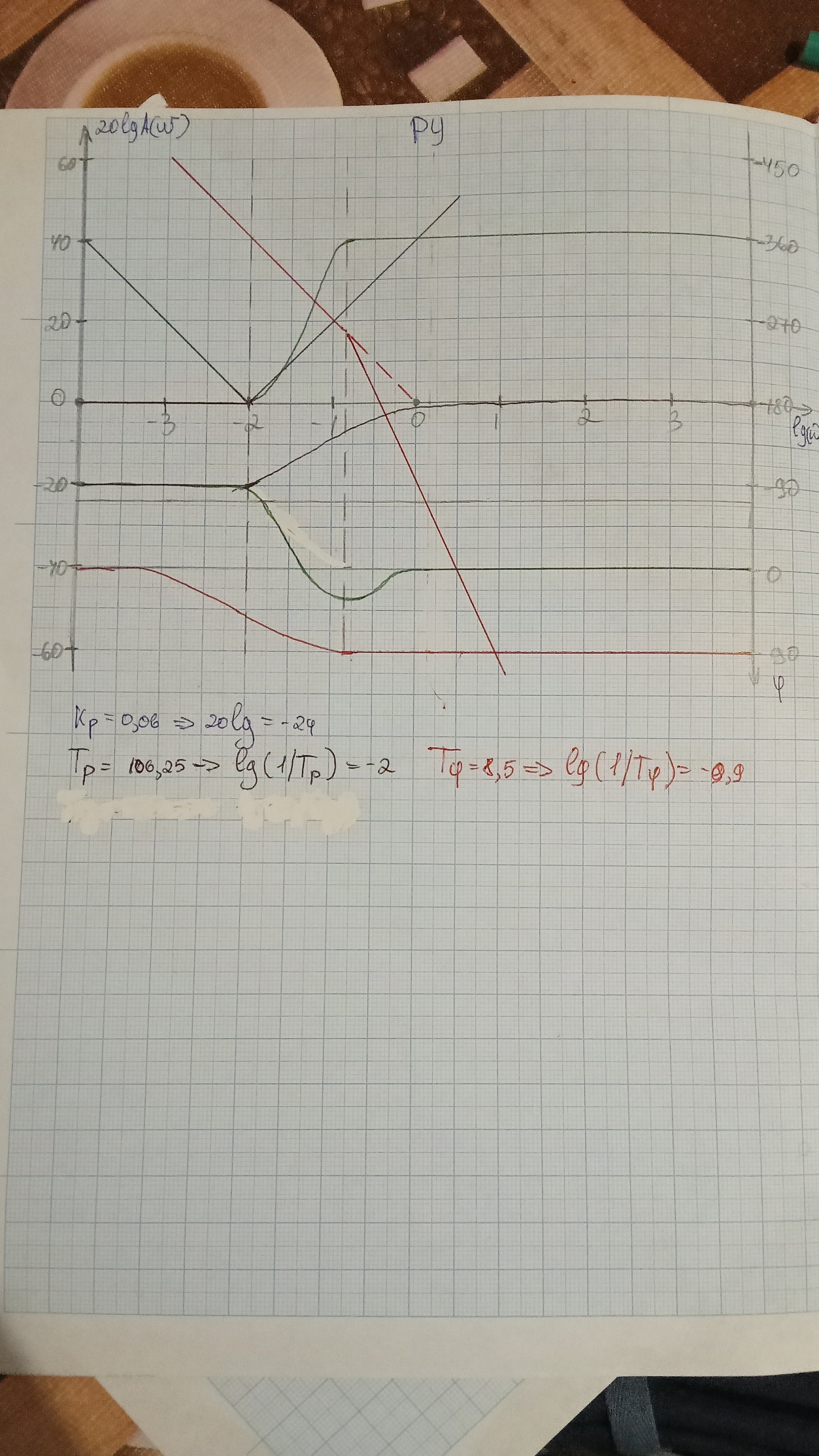
ЛАЧХ
Частота среза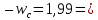
Запас по фазе = 
°
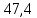Запас по амплитуде =37,5
Заключение
В процессе написания курсовой работы была исследована теоретическая система автоматического регулирования в соответствии с предложенной схемой, проведено исследование отдельных частей системы – объекта регулирования и регулирующего устройства. Построены частотные графики составных частей системы, а также графики разомкнутой системы, некоторые из которых понадобились для изучения устойчивости системы. В конечном итоге, было выяснено, что система является устойчивой. В последствии были подобраны такие коэффициенты, что система, после изучения оказалась устойчивой и соответствовала требованиям качества.
| |  |  |  |  |
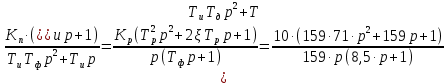
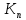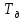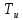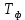| Было | 10 | 71 | 159 | 8,5 |
| Стало | 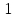 | 71 | 159 | 0,01 |
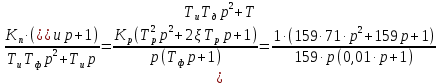
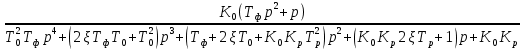
Таким образом, характеристический полином имеет вид:
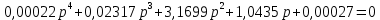
График переходного процесса
Система стала более качественной, так как перерегулирование практически отсутствует
Т.к. количество колебаний не превышает трёх – система качественна.
Рассмотрим критерий устойчивости Рауса-Гурвица.
Для определения устойчивости системы составим матрицу Гурвица, учитывая коэффициенты характеристического полином.
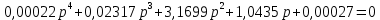
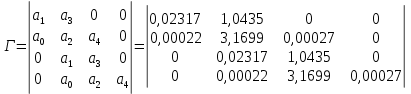
Из данной матрицы имеем диагональные миноры:
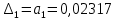
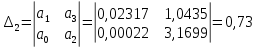
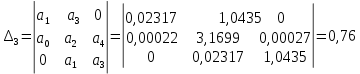
Можно сделать вывод, что система устойчива, т.к. диагональные миноры больше нуля.
Рассмотрим критерий устойчивости Липатова-Соколова
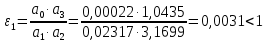
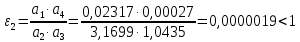
Делаем вывод, что
система устойчива, т.к. удовлетворяет неравенству.
Рассмотрим критерий устойчивости Михайлова
Выполним замену в характеристическом полиноме p=i∙w
Получим:
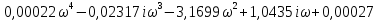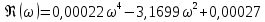
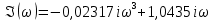
= 0 Так как
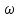
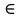[0;+∞), отрицательные значения рассматривать не будем. Составим таблицу значений:
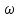| | 0 | 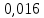 | 0,1 | 0,25 | 0,447 | 1,2 | 1,8 | 5 | 6,387 |
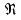 | 0,00027 | 0 | -0,4 | -2,55 | -8,14 | -57 | -122,3 | -397 | 0 |
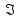 | 0 | 0,016 | 0,094 | 0,17 | 0 | -7,46 | -27,3 | -617 | -1286 |
В приближении
-0,004 -0,003 -0,002 -0,001 0 0,001
Годограф обходит квадранты последовательно, имеет спиралевидной форму, следовательно - система устойчива
Корневой критерий качества
Быстродействие системы определяется степенью устойчивости η – так называется расстояние мнимой оси до ближайшего корня (или пары комплексно-сопряженных корней).
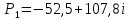
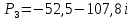
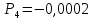
Система устойчива, т.к. действительные части комплексных корней лежат в левой полуплоскости
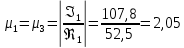
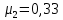
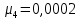
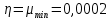
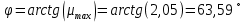
Запас устойчивости
Обратимся к годографу Найквиста (АФЧХ замкнутой системы)
Запас по фазе:
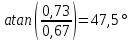
Для определения запаса по амплитуде необходимо найти расстояние от (-1;0) до точки пересечения с этой же полуосью
В практических задачах нужно обеспечивать запас по амплитуде не менее 6 дБ
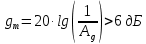
Чтобы выполнялось данное условие, необходимо, чтобы
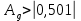
Для нашего случая – это условие выполняется
Запасы устойчивости по ЛАФЧХ
ЛФЧХ
ЛАЧХ
Частота среза
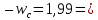Запас по фазе = 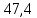°Запас по амплитуде =37,5
Заключение
В процессе написания курсовой работы была исследована теоретическая система автоматического регулирования в соответствии с предложенной схемой, проведено исследование отдельных частей системы – объекта регулирования и регулирующего устройства. Построены частотные графики составных частей системы, а также графики разомкнутой системы, некоторые из которых понадобились для изучения устойчивости системы. В конечном итоге, было выяснено, что система является устойчивой. В последствии были подобраны такие коэффициенты, что система, после изучения оказалась устойчивой и соответствовала требованиям качества.