МИНИСТЕРСТВО ЗДРАВООХРАНЕНИЯ ДОНЕЦКОЙНАРОДНОЙ РЕСПУБЛИКИ

ГОСУДАРСТВЕННАЯ ОБРАЗОВАТЕЛЬНАЯ ОРГАНИЗАЦИЯВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ ИМЕНИ М.ГОРЬКОГО»

МЕДИКО-ФАРМАЦЕВТИЧЕСКИЙ ФАКУЛЬТЕТА

Кафедра Фармацевтической и медицинской химии

Контрольная работа №2

по Физической и коллоидной химии

Вариант № 13

Беловой (Неживенко) Виолетты Александровны

курс 3 группа 3

Форма обучения заочная

Донецк 2023

Вариант 13

 

Задача 1

Реакция омыления уксусно-этилового эфира гидроксидом калия является реакцией второго порядка. Через 30 мин после начала реакции концентрация щелочи составила 0,07 моль/л. Сколько времени нужно, чтобы исходные вещества прореагировали на 70%, если начальные концентрации их одинаковы и составляют 0,12 моль/л?
Дано:

n = 2;

t = 30 мин;

С = 0,07 моль/л;

С_о = 0,12 моль/л;

α = 0,7 (70 %).

Найти:

t₁ - ?

Решение:

1. 
   Для реакций второго порядка кинетическое уравнение имеет вид:
   

kt = 1/C – 1/C_о,

откуда можно найти константу скорости реакции

k = (1/C – 1/C_о) / t = (1/0,07 – 1/0,12) / 30 = 0,1984 л/(моль·мин).

2. 
   Если исходные вещества прореагировали на 70%, то концентрация станет равной
   

С₁ = С_о(1 – α) = 0,12·(1-0,7) = 0,036 моль/л.

Тогда

t₁ = (1/ С₁ – 1/C_о) / k = (1/0,036 – 1/0,12) / 0,1984 = 98 мин.
Ответ: понадобится 98 минут.

Задача 2

Для приготовления лекарственной мази на основе бентонита, необходимо определить дисперсность частиц бентонита согласно данным: время оседания частиц в водной среде на расстояние 10 см составляет 2,35∙10⁵ с, плотность бентонита – 2,1 г/см³, плотность среды – 1,1 г/см³, вязкость среды – 2∙10^-3 Па∙с (форма частиц сферическая).

Дано:

t₁ = 2,35∙10⁵ с;

h = 10 см = 0,1 м;

ρ = 2,1 г/см³;

ρ_о = 1,1 г/см³;

η = 2∙10^-3 Па∙с.

Найти:

D - ?

Решение:

 Из уравнения Стокса

---

,

откуда

D² = 2t₁·(ρ – ρ_о)·g / 36ηh =

= 2·2,35∙10⁵·(2,1– 1,1)·10³·9,81 / 36·2∙10^-3·0,1 = 6,4·10¹¹ м^-2.

Окончательно


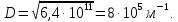
Ответ: D =

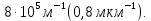
Задача 3

При медленном капельном введении MgCl₂ в разбавленный раствор NaOH возможно образование гидрозоля. Напишите формулу мицеллы. К какому электроду будет двигаться гранула этого золя? Какой электролит будет наилучшим коагулянтом  этого золя: KCl; (CH₃COO)₂Zn; AlI₃?

 

Ответ:

Уравнение реакции образования гидрозоля:

MgCl₂ + 2NaOH = Mg(OH)₂↓ + 2NaCl.

При такой технике получения золя гидроксида магния в избытке будет щелочь

NaOH  Na⁺ + OH^-.

Тогда формула мицеллы будет следующая:

{m[Mg(OH)₂]·nOH^-·(n–x)Na⁺}^x-·xNa⁺.

Знак заряда коллоидных частиц этого золя – отрицательный, значит, частицы будут двигаться к аноду (положительному электроду) при электрофорезе.

Коагулирующим действием будут обладать ионы, знак заряда которых противоположен заряду коллоидной частицы, значит, это будут катиону. Из предложенного рядка электролитов KCl, (CH₃COO)₂Zn, AlI₃ имеем три вида катионов: K⁺, Zn²⁺ и Al³⁺. Коагулирующее действие иона тем выше, чем выше его заряд, значит, самым эффективным коагулянтом будет AlI₃.

Задача 4

При адсорбции нитроглицерина из водных растворов на глине определите константы в уравнении Фрейндлиха по следующим экспериментальным данным

w, %	0,14	0,23	0,47	0,66	0,99	1,3
Г∙103, кг/кг	4,00	11,00	21,00	23,00	36,00	39,00

---

 

Решение:

Эмпирическое уравнение Фрейндлиха для адсорбции имеет вид:

,

где А – удельная адсорбция; р – равновесное давление; b и n – константы, определяемые опытным путем.

Константы уравнения Фрейндлиха из опытных данных определяют графически. Для этого уравнение Фрейндлиха логарифмируют:



Затем строят линейную зависимость в координатах lgA–lg p (вместо давления будем использовать величину концентрации). Экстраполяция зависимости до оси ординат дает отрезок, равный lgb, тангенс угла наклона прямой равен:

.

Если построить график с помощью программы Excel, то можно вывести линию тренда и уравнение прямой, из которого найти константы уравнения Фрейндлиха. Выполним дополнительные расчеты и построим график

С, %	Г, кг/кг	lgC	lgГ
0,14	0,004	-0,85	-2,40
0,23	0,011	-0,64	-1,96
0,47	0,021	-0,33	-1,68
0,66	0,023	-0,18	-1,64
0,99	0,036	0,00	-1,44
1,3	0,039	0,11	-1,41

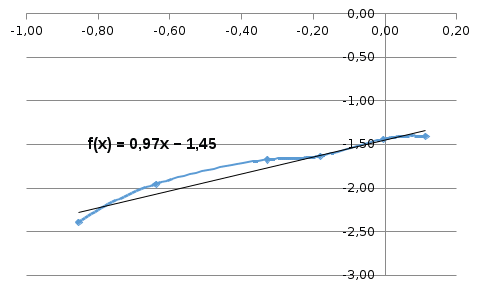
Как видно, из уравнения прямой

1/n = tgα = 0,969,

lgb = -1,4488, откуда b = 10^-1,4488 = 0,0356.
Ответ: 1/n = 0,969, b = 0,0356.
Теоретический вопрос

---

Адсорбция на пористых адсорбентах растворов средней концентрации. Эмпирическое уравнение Фрейндлиха.
Ответ:

Пористые тела относятся к связаннодисперсным системам типа «твердое тело – газ». Наличие развитой внутренней межфазной поверхности обуславливает высокую адсорбционную способность натуральных и синтетических пористых тел. К пористым телам относят такие распространенные адсорбенты, как активированные угли, силикагели, алюмогели, цеолиты.

В зависимости от дисперсности пористые тела делят на три класса:

1) макропористые тела с радиусом пор более 100 нм;

2) переходнопористые тела с радиусом пор 1,5–100 нм;

3) микропористые тела с радиусом пор 0,5–1,5 нм.

Пористость и дисперсность определяют удельную поверхность адсорбентов, с увеличением которой возрастает количество извлекаемого вещества адсорбата на единицу массы адсорбента. Большинство промышленных пористых адсорбентов представляют собой полидисперсные системы, характеризуемых следующими количественными показателями:

1) пористость (порозность)

2) истинная плотность

r_и = m / (V_общ - V_пор);

3) кажущаяся плотность

r_к = m / V_общ.

При адсорбции газов и растворенных веществ на макропористых адсорбентах диаметр пор значительно больше радиуса молекул адсорбата. Поэтому стенки пор в данном случае могут быть рассмотрены как гладкие поверхности. Таким образом, для описания закономерностей адсорбции на макропористых адсорбентах применима теория мономолекулярной адсорбции Ленгмюра.

Для переходнопористых тел при малых давлениях паров адсорбата характерна полимолекулярная адсорбция, а при увеличении равновесного давления наблюдается капиллярная конденсация.

Для термодинамического описания полимолекулярной адсорбции в переходнопористых телах применяется потенциальная теория Поляни. Модель адсорбции в теории Поляни предполагает, что адсорбат ведет себя термодинамически как однокомпонентная система, находящаяся в поле поверхностных сил адсорбента, который химически инертен. В адсорбционном пространстве действуют только дисперсионные силы, которые имеют аддитивный характер, т.е. при адсорбции характер взаимодействия между молекулами адсорбата не изменяется, а происходит лишь увеличение его плотности на поверхности адсорбента. Интенсивность действия дисперсионных сил не зависит от температуры. Также в данной теории сделано допущение о том, что вещество адсорбата находится в поверхностных слоях адсорбента в жидком (конденсированном) состоянии.

---

Допущения, сделанные в теории полимолекулярной адсорбции Поляни в значительной степени характеризуют состояние вещества адсорбата в порах адсорбента. В связи с этим данная теория наиболее пригодна для описания адсорбционных процессов на пористых адсорбентах, в порах которых происходит конденсация паров.

Основной количественной характеристикой полимолекулярной адсорбции в пористых адсорбентах является объем жидкого адсорбата:

V = AV_M,

где V_M – молярный объем адсорбата в жидком состоянии, м³/моль.

Мерой интенсивности адсорбционного взаимодействия принят адсорбционнй потенциал – работа переноса 1 моль пара, находящегося в равновесии с жидким адсорбатом в отсутствии адсорбента (при давлении насыщения р_s), в равновесную с адсорбентом паровую фазу, характеризующуюся равновесным давлением адсорбции р:

e = RTln(p / р_s).

Каждой точке изотермы адсорбции соответствуют определенные значения А и ln (p / р_s), по которым можно рассчитать значения V и e. Функциональная зависимость адсорбционного потенциала от объема адсорбированного вещества получила название потенциальной кривой адсорбции. Для одного пористого адсорбента и группы адсорбатов-гомологов справедливо выражение:

e / e₀ = b.

где e₀ – адсобционный потенциал адсорбата, принятого за стандарт;

b – коэффициент аффинности.

Эмпирическое уравнение Фрейндлиха для адсорбции имеет вид:

,

где А – удельная адсорбция; р – равновесное давление; b и n – константы, определяемые опытным путем.

Константа b по своему физическому смыслу – значение адсорбции при равновесной концентрации адсорбата, равной единице (при С = 1, А = b). Эта константа для различных адсорбционных систем изменяется в пределах 2÷2,5. Показатель 1/n характеризует степень отклонения изотермы адсорбции от прямой линии (1/n ≈ 0,2–0,7).

Константы уравнения Фрейндлиха из опытных данных определяют графически. Для этого уравнение Фрейндлиха логарифмируют:



Затем строят линейную зависимость в координатах lgA–lg p (рисунок 1). Экстраполяция зависимости до оси ординат дает отрезок, равный lgb, тангенс угла наклона прямой равен tgα = 1/n.

---

Смотрите также файлы

• Японский Император Ханадзоно (1308 1318) был 96м Императором Японии. Он родился 14 марта 1297 года, сыном Императора Фусано.docx

• Леонардо да Винчи первый в мире инженер, которому приписывают проекты пилотируемого полета.docx

• Пояснительная записка к дипломному проекту на тему Снижение степени загрязнения окружающей среды отходами переработки хлопка Студент.docx

• Цессия в гражданском праве.doc

• Лекция производные хиноксалина хиноксидин (таблетки).pptx