ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 28
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
т, можно для газа и пара найти уточненные значения 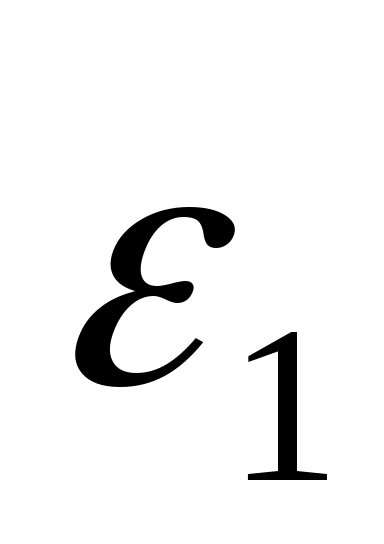 ,
, 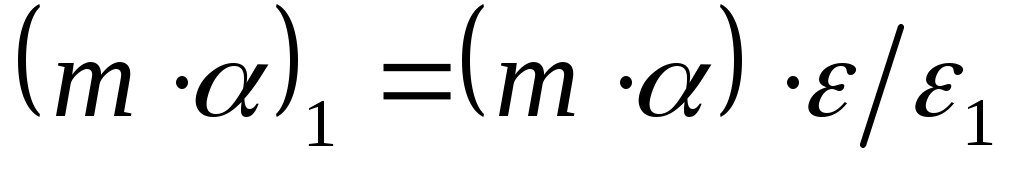 и по
и по 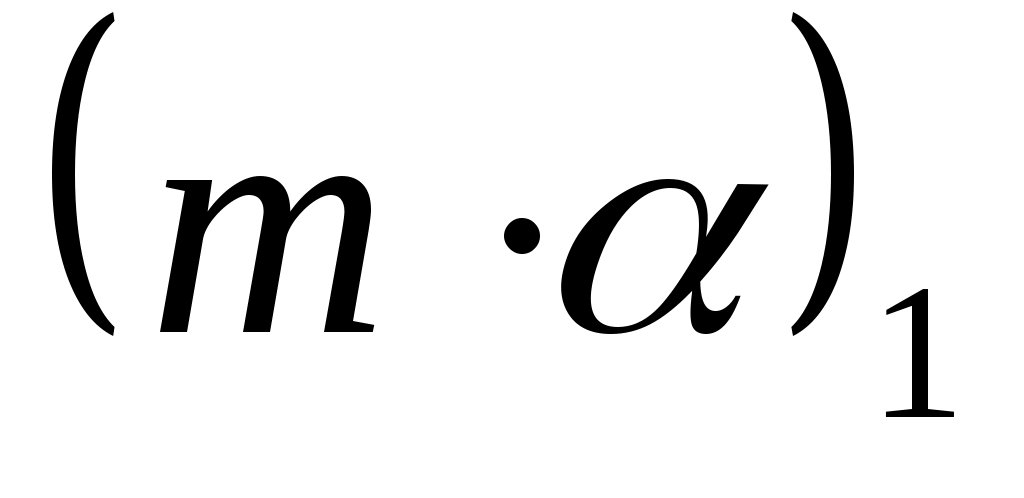 , уточненные значения
, уточненные значения  и затем т и d.
и затем т и d.
Подставляя все полученные значения в правую часть формул (43) или (44), определяют расход QM или QО. Если эти значения отличаются от принятых предельных значений шкал дифманометров не более чем на 0,2 %, то расчет считается правильным. В противном случае необходимо скорректировать значение d.
Второй тип задачи. Он отличается от предыдущего только тем, что не задан предельный перепад давления дифманометра и надо выбирать его из ряда: 1; 1,6; 2,5; ...; 1600; 2500 кгс/м2 и далее из ряда 0,4; 0,63; ...; 6,3; 10,0 кгс/см2. При этом возможны два варианта.
и надо выбирать его из ряда: 1; 1,6; 2,5; ...; 1600; 2500 кгс/м2 и далее из ряда 0,4; 0,63; ...; 6,3; 10,0 кгс/см2. При этом возможны два варианта.
Несмотря на все перечисленные преимущества малых т бывают случаи, когда необходимо их увеличивать (вплоть до самых больших допустимых значений).
Во-первых, это необходимо, когда надо максимально снизить потерю давления. Во-вторых, при очень большой скорости движения пара в трубах (что характерно для паропроводов высокого давления), когда даже при самых больших получаются
значительные т. В-третьих, при измерении расхода газа или пара, когда надо стремиться к минимуму суммы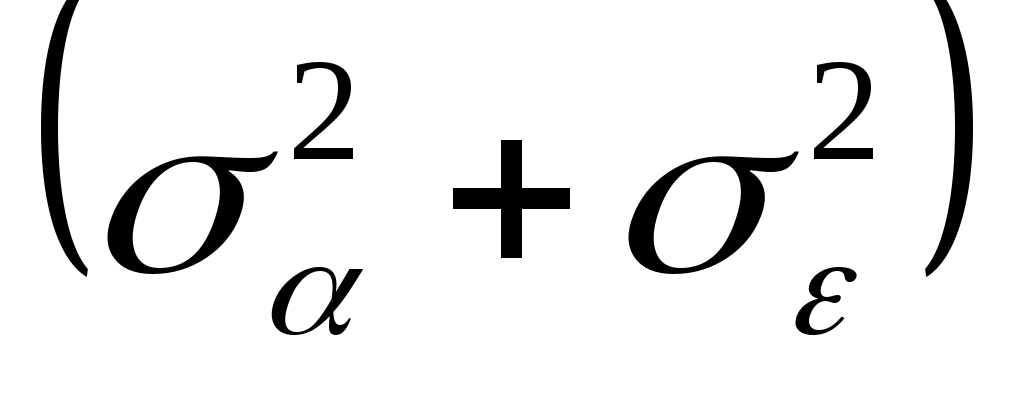 [10,16, 8], а при этом с возрастанием
[10,16, 8], а при этом с возрастанием 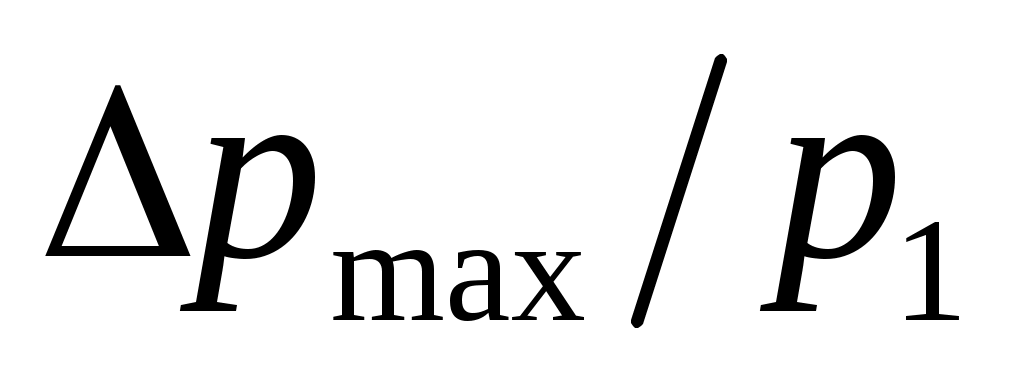 увеличивается
увеличивается 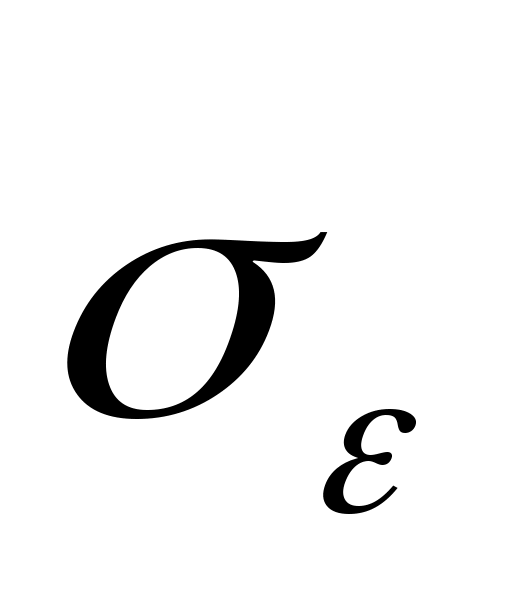 , иногда при больших
, иногда при больших  выгодно уменьшить это отношение путем незначительного увеличения т. В случае применения вычислительной техники и при учете изменения ε вместе с перепадом
выгодно уменьшить это отношение путем незначительного увеличения т. В случае применения вычислительной техники и при учете изменения ε вместе с перепадом  необходимость в этом увеличении т отпадает.
необходимость в этом увеличении т отпадает.
Дополнительные указания по выбору оптимального значения т содержатся в работах [8, 21, 30, 31].
Для удобства определения , обеспечивающего или непревышение допустимой потери давления
, обеспечивающего или непревышение допустимой потери давления  , или получение желаемого т, в правилах 28-64 была разработана номограмма, которая принята также и в правилах РД 50-213-80. Ее схема представлена на рис. 21. На оси ординат отложены значения
, или получение желаемого т, в правилах 28-64 была разработана номограмма, которая принята также и в правилах РД 50-213-80. Ее схема представлена на рис. 21. На оси ординат отложены значения , а на оси абсцисс значение С, полученное из уравнений (43) и (44). Эти уравнения могут быть представлены в виде
, а на оси абсцисс значение С, полученное из уравнений (43) и (44). Эти уравнения могут быть представлены в виде
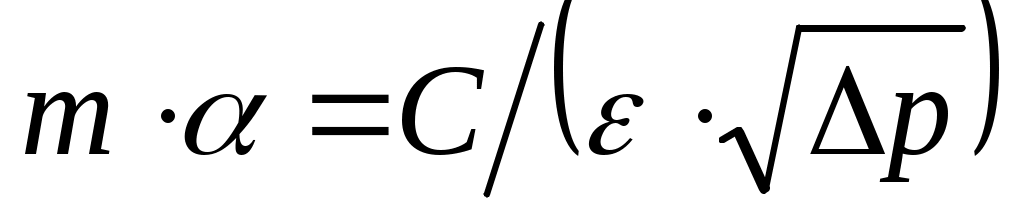 (50)
(50)
где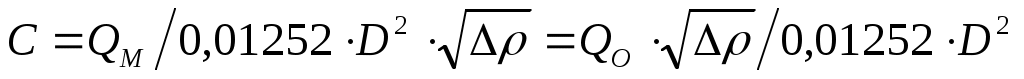
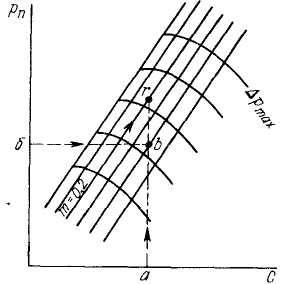 Рис. 21. Номограмма для определения
Рис. 21. Номограмма для определения 
На номограмме приведены наклонные параллельные линии, каждая из которых соответствует определенному значению т,
и дуги, соответствующие определенным
Если задана предельно допустимая потеря давления , то от этого значения
, то от этого значения  (точка б на рис. 21) надо по горизонтали провести линию до пересечения с вертикалью, которая начинается от определенного по уравнению (50) значения С (точка а на рис. 21). На пересечении горизонтали и вертикали получим точку
(точка б на рис. 21) надо по горизонтали провести линию до пересечения с вертикалью, которая начинается от определенного по уравнению (50) значения С (точка а на рис. 21). На пересечении горизонтали и вертикали получим точку 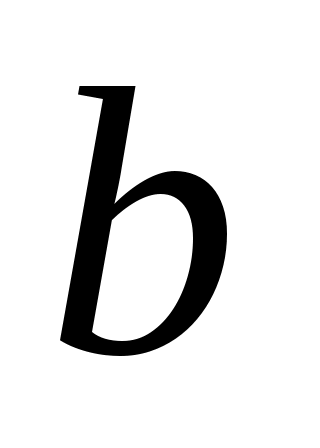 . Если эта точка расположена между двумя дугами, то принимают значение
. Если эта точка расположена между двумя дугами, то принимают значение  , соответствующее нижней дуге, и на ее пересечении с вертикалью, идущей от точки а, получают соответствующее значение т.
, соответствующее нижней дуге, и на ее пересечении с вертикалью, идущей от точки а, получают соответствующее значение т.
Если потеря давления не задана, то вертикаль, идущую от точки а, продолжают до пересечения с наклонной линией выбранного т, например с линией т = 0,2 (точка
не задана, то вертикаль, идущую от точки а, продолжают до пересечения с наклонной линией выбранного т, например с линией т = 0,2 (точка 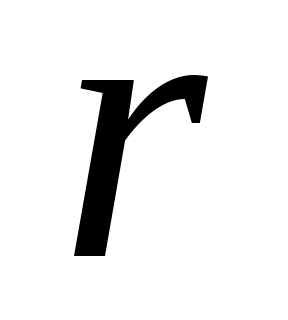 на рис. 21), и принимают значение
на рис. 21), и принимают значение  , соответствующее ближайшей дуге (верхней или нижней). На пересечении дуги с вертикалью от точки а находится уточненное значение т.
, соответствующее ближайшей дуге (верхней или нижней). На пересечении дуги с вертикалью от точки а находится уточненное значение т.
Определить можно и аналитически [22 ] без помощи рассмотренной номограммы.
можно и аналитически [22 ] без помощи рассмотренной номограммы.
После выбора расчет проводят по первому типу задачи (см. стр. 50), т. е. последовательно определяют
расчет проводят по первому типу задачи (см. стр. 50), т. е. последовательно определяют  ,
,  , m и d.
, m и d.
Изложенный метод расчета соответствует рекомендуемому как правилами РД 50-213-80, так и правилами 28-64. Отличие этих правил друг от друга состоит не в методике расчета, а лишь в способе определения значения коэффициента расхода .
.
Если нет таблиц или кривых, связывающих значения
 со значениями
со значениями  или т, то после нахождения по номограмме (рис. 21) значения т по формулам, приведенным в правилах РД 50-213-80, определяют соответствующее значение, а затем произведение
или т, то после нахождения по номограмме (рис. 21) значения т по формулам, приведенным в правилах РД 50-213-80, определяют соответствующее значение, а затем произведение  . После этого находят в процентах отклонение
. После этого находят в процентах отклонение 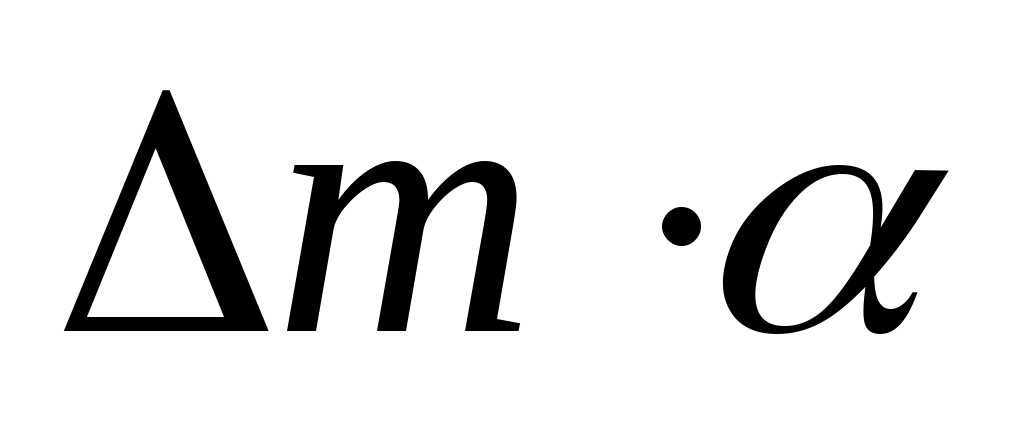 этого произведения от значения, определенного по формуле (50). Затем изменяют значение т на величину этого отклонения, взятого с обратным знаком, с ориентировочным учетом происходящего при этом изменения значения
этого произведения от значения, определенного по формуле (50). Затем изменяют значение т на величину этого отклонения, взятого с обратным знаком, с ориентировочным учетом происходящего при этом изменения значения  . Для малых
. Для малых 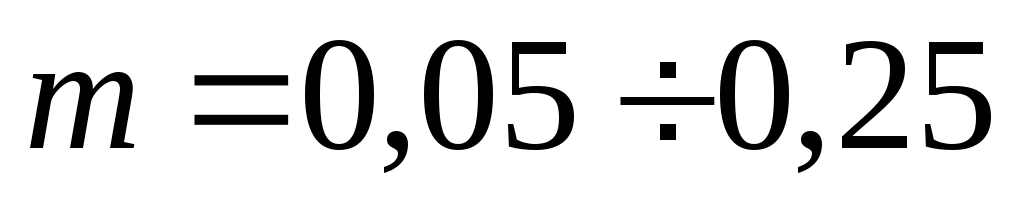 изменением
изменением  можно пренебречь, а при больших
можно пренебречь, а при больших 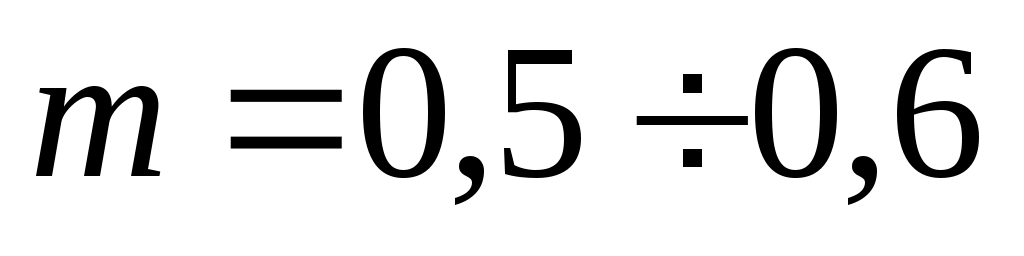 это изменение можно оценить в 25—30 % от
это изменение можно оценить в 25—30 % от 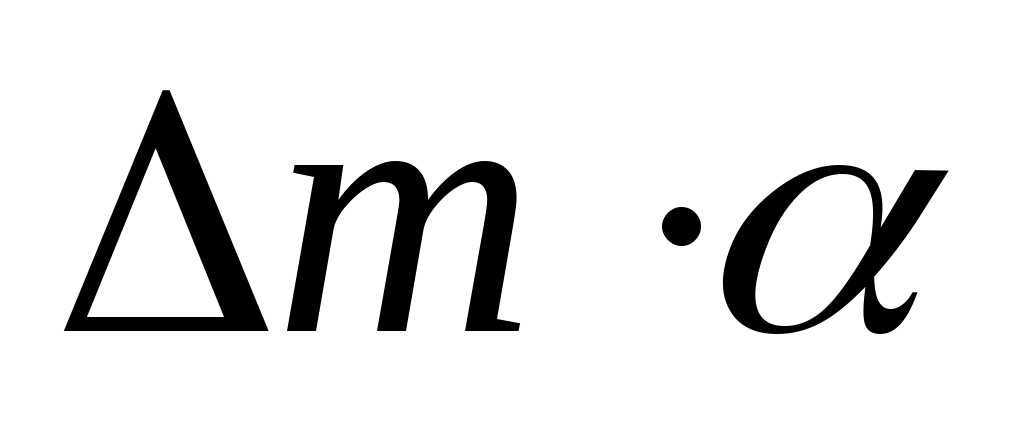 . Таким способом [16] можно довольно быстро (в одно-два приближения) получить окончательное значение произведения
. Таким способом [16] можно довольно быстро (в одно-два приближения) получить окончательное значение произведения  , соответствующее формуле (50).
, соответствующее формуле (50).
Подставляя все полученные значения в правую часть формул (43) или (44), определяют расход QM или QО. Если эти значения отличаются от принятых предельных значений шкал дифманометров не более чем на 0,2 %, то расчет считается правильным. В противном случае необходимо скорректировать значение d.
Второй тип задачи. Он отличается от предыдущего только тем, что не задан предельный перепад давления дифманометра
-
Задана предельно допустимая потеря давления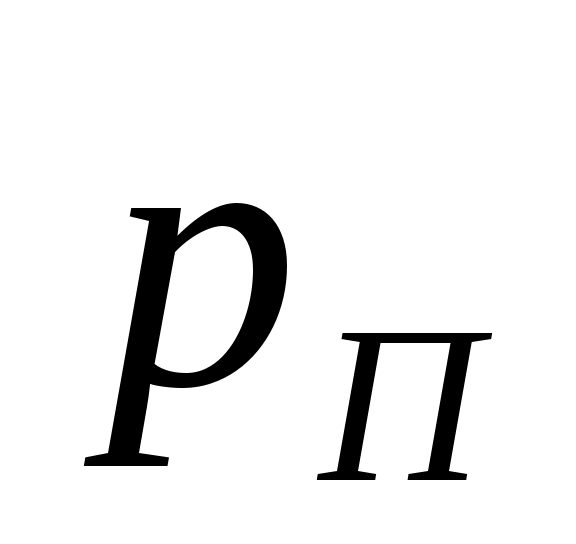 . Чем она меньше, тем меньше надо брать
. Чем она меньше, тем меньше надо брать  и тем больше будет относительная площадь сужающего устройства т.
и тем больше будет относительная площадь сужающего устройства т. -
Предельно допустимая потеря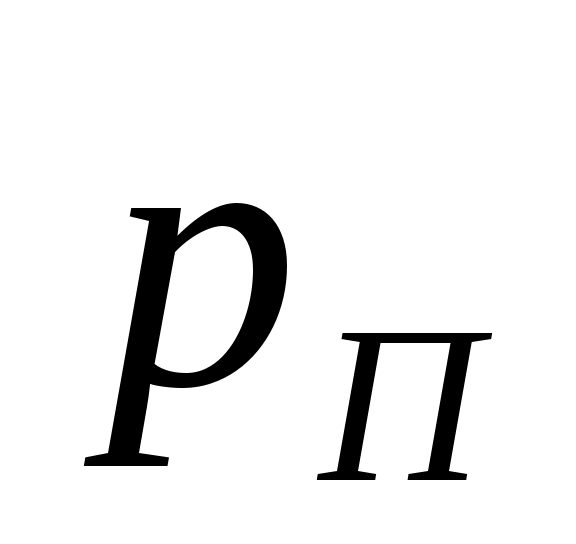 не задана. Тогда
не задана. Тогда  следует выбирать так, чтобы получить наиболее целесообразное значение т. В большинстве случаев (для стандартных диафрагм и сопел) выгодно иметь небольшое значение т, находящееся в пре делах от 0,1 до 0,3. Обычно эти значения т соответствуют
следует выбирать так, чтобы получить наиболее целесообразное значение т. В большинстве случаев (для стандартных диафрагм и сопел) выгодно иметь небольшое значение т, находящееся в пре делах от 0,1 до 0,3. Обычно эти значения т соответствуют  , изменяющихся в пределах от 0,16 до 0,63 кгс/см2. При этом полу чаем преимущества, перечисленные ниже. Увеличивается точность измерения расхода, так как уменьшается средняя квадратическая погрешность
, изменяющихся в пределах от 0,16 до 0,63 кгс/см2. При этом полу чаем преимущества, перечисленные ниже. Увеличивается точность измерения расхода, так как уменьшается средняя квадратическая погрешность  исходного коэффициента расхода; снижается влияние на
исходного коэффициента расхода; снижается влияние на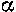 шероховатости трубопровода и возрастает постоянство
шероховатости трубопровода и возрастает постоянство  в пределах шкалы прибора, увеличивается область измерения, потому что с уменьшением т существенно уменьшается значение нижней границы числа Re, начиная от которого допускается применение стандартных диафрагм и сопел; сокращается необходимая длина прямого участка трубопровода, так как уменьшается влияние на коэффициент расхода α деформации потока местными сопротивлениями. Кроме того, уменьшение величины т связано с возрастанием
в пределах шкалы прибора, увеличивается область измерения, потому что с уменьшением т существенно уменьшается значение нижней границы числа Re, начиная от которого допускается применение стандартных диафрагм и сопел; сокращается необходимая длина прямого участка трубопровода, так как уменьшается влияние на коэффициент расхода α деформации потока местными сопротивлениями. Кроме того, уменьшение величины т связано с возрастанием  . В результате уменьшается постоянная времени дифманометра и возрастает его быстродействие, снижается влияние воздушных пузырей или водяных пробок в импульсных линиях, а также нарушения равенства высот столбов жидкости в них.
. В результате уменьшается постоянная времени дифманометра и возрастает его быстродействие, снижается влияние воздушных пузырей или водяных пробок в импульсных линиях, а также нарушения равенства высот столбов жидкости в них.
Несмотря на все перечисленные преимущества малых т бывают случаи, когда необходимо их увеличивать (вплоть до самых больших допустимых значений).
Во-первых, это необходимо, когда надо максимально снизить потерю давления. Во-вторых, при очень большой скорости движения пара в трубах (что характерно для паропроводов высокого давления), когда даже при самых больших получаются
значительные т. В-третьих, при измерении расхода газа или пара, когда надо стремиться к минимуму суммы
Дополнительные указания по выбору оптимального значения т содержатся в работах [8, 21, 30, 31].
Для удобства определения
где
 Рис. 21. Номограмма для определения
Рис. 21. Номограмма для определения На номограмме приведены наклонные параллельные линии, каждая из которых соответствует определенному значению т,
и дуги, соответствующие определенным
Если задана предельно допустимая потеря давления
Если потеря давления
Определить
После выбора
Изложенный метод расчета соответствует рекомендуемому как правилами РД 50-213-80, так и правилами 28-64. Отличие этих правил друг от друга состоит не в методике расчета, а лишь в способе определения значения коэффициента расхода
Если нет таблиц или кривых, связывающих значения
| № п/п | m2 | m | Re=104 | Re=2 104 | Re=3 104 | Re=5 104 | Re=105 | Re=106 | Re=2 107 | Re=108 | ||||||||
| α | m α | α | m α | α | m α | α | m α | α | m α | α | m α | α | m α | α | m α | |||
| 1 | 0,0025 | 0,0500 | 0,6031 | 0,03015 | 0,6022 | 0,03011 | 0,6018 | 0,03009 | 0,6015 | 0,03007 | 0,6013 | 0,03006 | 0,6010 | 0,03005 | 0,6009 | 0,03004 | 0,6009 | 0,03004 |
| 2 | 0,0030 | 0,05477 | 0,6035 | 0,03305 | 0,6025 | 0,03300 | 0,6020 | 0,03298 | 0,6017 | 0,03296 | 0,6015 | 0,03295 | 0,6011 | 0,03292 | 0,6010 | 0,03291 | 0,6010 | 0,03291 |
| 3 | 0,0040 | 0,06325 | 0,6041 | 0,03821 | 0,6029 | 0,03812 | 0,6025 | 0,03811 | 0,6021 | 0,03808 | 0,6017 | 0,03806 | 0,6013 | 0,03803 | 0,6012 | 0,03802 | 0,6011 | 0,03802 |
| 4 | 0,0050 | 0,07071 | 0,6049 | 0,04277 | 0,6035 | 0,04267 | 0,6030 | 0,04263 | 0,6025 | 0,04260 | 0,6021 | 0,04257 | 0,6016 | 0,04254 | 0,6015 | 0,04253 | 0,6014 | 0,04253 |
| 5 | 0,0100 | 0,10000 | 0,6084 | 0,06084 | 0,6062 | 0,06062 | 0,6054 | 0,06054 | 0,6046 | 0,06046 | 0,6040 | 0,06040 | 0,6032 | 0,06032 | 0,6031 | 0,06031 | 0,6031 | 0,06031 |
| 6 | 0,0200 | 0,14142 | 0,6145 | 0,08690 | 0,6112 | 0,08644 | 0,6099 | 0,08625 | 0,6080 | 0,08610 | 0,6078 | 0,08596 | 0,6067 | 0,08580 | 0,6065 | 0,08577 | 0,6063 | 0,08575 |
| 7 | 0,0300 | 0,17321 | 0,6206 | 0,1075 | 0,6164 | 0,1068 | 0,6148 | 0,1064 | 0,6133 | 0,1062 | 0,6127 | 0,1061 | 0,6105 | 0,1057 | 0,6102 | 0,1057 | 0,6102 | 0,1057 |
| 8 | 0,0400 | 0,20000 | 0,6265 | 0,1253 | 0,6214 | 0,1243 | 0,6195 | 0,1239 | 0,6177 | 0,1235 | 0,6162 | 0,1232 | 0,6144 | 0,1229 | 0,6140 | 0,1228 | 0,6140 | 0,1228 |
| 9 | 0,0500 | 0,22361 | 0,6321 | 0,1413 | 0,6263 | 0,1400 | 0,6240 | 0,1395 | 0,6220 | 0,1391 | 0,6202 | 0,1387 | 0,6181 | 0,1382 | 0,6177 | 0,1381 | 0,6177 | 0,1381 |
| 10 | 0,0600 | 0,24495 | 0,6377 | 0,1562 | 0,6311 | 0,1546 | 0,6285 | 0,1539 | 0,6263 | 0,1534 | 0,6243 | 0,1529 | 0,6219 | 0,1523 | 0,6215 | 0,1522 | 0,6214 | 0,1522 |
| 11 | 0,0700 | 0,26458 | 0,6431 | 0,1701 | 0,6358 | 0,1682 | 0,6330 | 0,1675 | 0,6305 | 0,1668 | 0,6283 | 0,1663 | 0,6257 | 0,1655 | 0,6251 | 0,1653 | 0,6250 | 0,1653 |
| 12 | 0,0800 | 0,28284 | 0,6485 | 0,1834 | 0,6405 | 0,1812 | 0,6374 | 0,1803 | 0,6347 | 0,1796 | 0,6323 | 0,1789 | 0,6291 | 0,1781 | 0,6288 | 0,1778 | 0,6287 | 0,1778 |
| 13 | 0,0900 | 0,30000 | 0,6538 | 0,1961 | 0,6451 | 0,1935 | 0,6418 | 0,1925 | 0,6388 | 0,1916 | 0,6362 | 0,1909 | 0,6331 | 0,1899 | 0,6325 | 0,1897 | 0,6324 | 0,1897 |
| 14 | 0,1000 | 0,31623 | 0,6589 | 0,2084 | 0,6496 | 0,2055 | 0,6461 | 0,2043 | 0,6429 | 0,2033 | 0,6401 | 0,2024 | 0,6367 | 0,2014 | 0,6361 | 0,2012 | 0,6360 | 0,2011 |
| 15 | 0,1100 | 0,33166 | 0,6641 | 0,2203 | 0,6542 | 0,2170 | 0,6504 | 0,2158 | 0,6470 | 0,2146 | 0,6440 | 0,2136 | 0,6405 | 0,2124 | 0,6398 | 0,2122 | 0,6397 | 0,2122 |
| 16 | 0,1200 | 0,34641 | 0,6693 | 0,2319 | 0,6588 | 0,2282 | 0,6547 | 0,2268 | 0,6511 | 0,2256 | 0,6480 | 0,2245 | 0,6442 | 0,2231 | 0,6435 | 0,2229 | 0,6434 | 0,2229 |
| 17 | 0,1300 | 0,36056 | 0,6745 | 0,2432 | 0,6633 | 0,2392 | 0,6591 | 0,2376 | 0,6552 | 0,2362 | 0,6519 | 0,2350 | 0,6479 | 0,2336 | 0,6472 | 0,2333 | 0,6470 | 0,2333 |
| 18 | 0,1400 | 0,37417 | 0,6796 | 0,2543 | 0,6679 | 0,2500 | 0,6634 | 0,2482 | 0,6593 | 0,2467 | 0,6559 | 0,2454 | 0,6516 | 0,2438 | 0,6508 | 0,2435 | 0,6507 | 0,2435 |
| 19 | 0,1500 | 0,38730 | 0,6847 | 0,2652 | 0,6724 | 0,2604 | 0,6677 | 0,2586 | 0,6634 | 0,2570 | 0,6598 | 0,2555 | 0,6553 | 0,2538 | 0,6545 | 0,2535 | 0,6544 | 0,2534 |
| 20 | 0,1600 | 0,40000 | 0,6899 | 0,2760 | 0,6770 | 0,2708 | 0,6720 | 0,2688 | 0,6676 | 0,2670 | 0,6637 | 0,2655 | 0,6591 | 0,2636 | 0,6582 | 0,2633 | 0,6581 | 0,2632 |
| 21 | 0,1700 | 0,41231 | 0,6950 | 0,2866 | 0,6815 | 0,2810 | 0,6764 | 0,2789 | 0,6717 | 0,2766 | 0,6677 | 0,2753 | 0,6628 | 0,2733 | 0,6619 | 0,2729 | 0,6618 | 0,2729 |
| 22 | 0,1800 | 0,42426 | 0,7002 | 0,2971 | 0,6861 | 0,2911 | 0,6807 | 0,2888 | 0,6756 | 0,2867 | 0,6717 | 0,2850 | 0,6666 | 0,2828 | 0,6657 | 0,2824 | 0,6655 | 0,2824 |
| 23 | 0,1900 | 0,43589 | 0,7053 | 0,3074 | 0,6907 | 0,3011 | 0,6851 | 0,2986 | 0,6800 | 0,2964 | 0,6756 | 0,2945 | 0,6704 | 0,2922 | 0,6694 | 0,2918 | 0,6693 | 0,2917 |
| 24 | 0,2000 | 0,44721 | 0,7105 | 0,3177 | 0,6953 | 0,3109 | 0,6894 | 0,3083 | 0,6842 | 0,3060 | 0,6797 | 0,3040 | 0,6742 | 0,3015 | 0,6732 | 0,3011 | 0,6730 | 0,3010 |
| 25 | 0,2100 | 0,45826 | 0,7157 | 0,3280 | 0,6999 | 0,3207 | 0,6939 | 0,3180 | 0,6884 | 0,3155 | 0,6837 | 0,3133 | 0,6780 | 0,3107 | 0,6770 | 0,3102 | 0,6768 | 0,3102 |
| 26 | 0,2200 | 0,46904 | 0,7209 | 0,3381 | 0,7046 | 0,3305 | 0,6983 | 0,3275 | 0,6927 | 0,3249 | 0,6878 | 0,3226 | 0,6819 | 0,3198 | 0,6808 | 0,3193 | 0,6806 | 0,3193 |
| 27 | 0,2300 | 0,47958 | 0,7261 | 0,3483 | 0,7092 | 0,3401 | 0,7027 | 0,3370 | 0,6969 | 0,3342 | 0,6919 | 0,3318 | 0,6858 | 0,3289 | 0,6847 | 0,3284 | 0,6845 | 0,3283 |
| 28 | 0,2400 | 0,48990 | 0,7314 | 0,3583 | 0,7139 | 0,3498 | 0,7072 | 0,3465 | 0,7012 | 0,3435 | 0,6960 | 0,3410 | 0,6897 | 0,3379 | 0,6886 | 0,3373 | 0,6883 | 0,3372 |
| 29 | 0,2500 | 0,50000 | 0,7368 | 0,3684 | 0,7187 | 0,3593 | 0,7117 | 0,3559 | 0,7055 | 0,3528 | 0,7001 | 0,3501 | 0,6936 | 0,3468 | 0,6925 | 0,3462 | 0,6923 | 0,3461 |
| 30 | 0,2600 | 0,50990 | 0,7421 | 0,3784 | 0,7235 | 0,3689 | 0,7163 | 0,3652 | 0,7099 | 0,3620 | 0,7043 | 0,3591 | 0,6976 | 0,3557 | 0,6964 | 0,3551 | 0,6962 | 0,3550 |
| 31 | 0,2700 | 0,51962 | 0,7475 | 0,3884 | 0,7283 | 0,3784 | 0,7209 | 0,3746 | 0,7143 | 0,3712 | 0,7085 | 0,3682 | 0,7016 | 0,3646 | 0,7003 | 0,3639 | 0,7002 | 0,3638 |
| 32 | 0,2800 | 0,52915 | 0,7529 | 0,3984 | 0,7331 | 0,3879 | 0,7255 | 0,3839 | 0,7187 | 0,3803 | 0,7128 | 0,3772 | 0,7057 | 0,3734 | 0,7044 | 0,3727 | 0,7042 | 0,3726 |
| 33 | 0,2900 | 0,53852 | 0,7584 | 0,4084 | 0,7380 | 0,,3974 | 0,7302 | 0,3932 | 0,7232 | 0,3895 | 0,7171 | 0,3862 | 0,7098 | 0,3822 | 0,7085 | 0,3815 | 0,7082 | 0,3814 |
| 34 | 0,3000 | 0,54772 | 0,7639 | 0,4184 | 0,7430 | 0,4069 | 0,7349 | 0,4025 | 0,7277 | 0,3986 | 0,7215 | 0,3952 | 0,7139 | 0,3910 | 0,7126 | 0,3903 | 0,7123 | 0,3902 |
| 35 | 0,3100 | 0,55678 | 0,7695 | 0,4284 | 0,7480 | 0,4165 | 0,7397 | 0,4118 | 0,7323 | 0,4077 | 0,7258 | 0,4041 | 0,7181 | 0,3999 | 0,7167 | 0,3990 | 0,7165 | 0,3989 |
| 36 | 0,3200 | 0,56569 | 0,7752 | 0,4385 | 0,7530 | 0,4260 | 0,7445 | 0,4212 | 0,7369 | 0,4169 | 0,7303 | 0,4131 | 0,7223 | 0,4086 | 0,7209 | 0,4078 | 0,7206 | 0,4077 |
| 37 | 0,3300 | 0,57446 | 0,7809 | 0,4486 | 0,7581 | 0,4355 | 0,7494 | 0,4305 | 0,7415 | 0,4260 | 0,7348 | 0,4221 | 0,7266 | 0,4174 | 0,7251 | 0,4166 | 0,7249 | 0,4164 |
| 38 | 0,3400 | 0,58310 | 0,7866 | 0,4587 | 0,7633 | 0,4451 | 0,7544 | 0,4397 | 0,7463 | 0,4352 | 0,7394 | 0,4311 | 0,7309 | 0,4262 | 0,7294 | 0,4253 | 0,7292 | 0,4252 |
| 39 | 0,3500 | 0,59161 | 0,7925 | 0,4688 | 0,7686 | 0,4547 | 0,7594 | 0,4492 | 0,7511 | 0,4444 | 0,7440 | 0,4401 | 0,7353 | 0,4350 | 0,7338 | 0,4341 | 0,7335 | 0,4340 |
| 40 | 0,3600 | 0,60000 | 0,7984 | 0,4791 | 0,7739 | 0,4643 | 0,7644 | 0,4587 | 0,7560 | 0,4536 | 0,7486 | 0,4492 | 0,7398 | 0,4439 | 0,7382 | 0,4429 | 0,7379 | 0,4428 |
| 41 | 0,3700 | 0,60828 | - | - | 0,7793 | 0,4740 | 0,7696 | 0,4681 | 0,7609 | 0,4629 | 0,7534 | 0,4583 | 0,7443 | 0,4528 | 0,7427 | 0,4518 | 0,7424 | 0,4516 |
| 42 | 0,3800 | 0,61644 | - | - | 0,7847 | 0,4837 | 0,7748 | 0,4776 | 0,7659 | 0,4721 | 0,7582 | 0,4674 | 0,7489 | 0,4617 | 0,7472 | 0,4606 | 0,7470 | 0,4605 |
| 43 | 0,3900 | 0,62450 | - | - | 0,7903 | 0,4935 | 0,7801 | 0,4872 | 0,7710 | 0,4815 | 0,7631 | 0,4766 | 0,7536 | 0,4706 | 0,7519 | 0,4695 | 0,7516 | 0,4694 |
| 44 | 0,4000 | 0,63246 | - | - | 0,7959 | 0,5034 | 0,7855 | 0,4968 | 0,7762 | 0,4909 | 0,7681 | 0,4858 | 0,7583 | 0,4796 | 0,7566 | 0,4785 | 0,7563 | 0,4783 |
| 45 | 0,4100 | 0,64031 | - | - | 0,8016 | 0,5133 | 0,7910 | 0,5065 | 0,7814 | 0,5004 | 0,7731 | 0,4950 | 0,7631 | 0,4886 | 0,7614 | 0,4875 | 0,7610 | 0,4873 |