Файл: 17. Какие задачи решаются с помощью дискретного преобразования Фурье.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 18
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
17. Какие задачи решаются с помощью дискретного преобразования Фурье?
Для чего предназначено прямое дискретное преобразование Фурье? Какими
свойствами должна обладать функция, используемая в качестве исходных данных
для прямого дискретного преобразования Фурье?
Преобразование Фурье позволяет представить любую функцию в виде набора гармонических сигналов. Преобразование Фурье лежит в основе методов свертки и проектировании цифровых корреляторов, активно применяется при спектральном анализе, используется при работе с длинными числами.
В классическом исполнении Преобразование Фурье основано на разложении исходной непрерывной функции времени на совокупность базисных гармонических функций. Дискретное преобразование, в свою очередь в качестве исходных данных использует дискретную функцию (дискретный или цифровой сигнал). Преобразование Фурье является функцией, описывающей амплитуду и начальную фазу гармонических функций, соответствующих определенной частоте. Результатом разложения сигнала в ряд Фурье является массив комплексных чисел. Как правило, комплексные числа результата преобразования Фурье представляются в виде массива значений модуля и массива значений аргумента. Значения модуля и аргумента обычно изображаются на двух отдельных графиках как функции частоты. Таким образом, из результата преобразования Фурье можно получить амплитудный и фазовый спектры сигналов.
Исходными данными для прямого преобразования Фурье является функция времени, т. е. представление сигнала во временной форме. Результатом прямого преобразования Фурье является изображение сигнала в частотной области. Для обратного, наоборот.
18. В какой форме представляется результат прямого дискретного
преобразования Фурье? Какую информацию содержит в себе результат прямого
дискретного преобразования Фурье? Как связан результат прямого дискретного
преобразования Фурье со спектром дискретного сигнала?
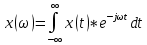
– форма записи ППФ, где x(t) – аналоговый сигнал; t – время;
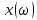– спектральная область сигнала (Фурье-образ); 
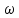- 2πf; f – частота; j – мнимая единица.Исходными данными для прямого преобразования Фурье является функция времени, т. е. представление сигнала во временной форме. Результатом прямого преобразования Фурье является изображение сигнала в частотной области. Количество комплексных чисел, полученных в результате прямого преобразования Фурье, всегда равно количеству отсчетов сигнала во временной форме. Например, если исходными данными для прямого преобразования Фурье служили 100 отсчетов сигнала, то результат будет содержать 100 комплексных чисел. Таким образом, мы будем располагать 100 отсчетами амплитудного спектра и 100 отсчетами фазового спектра сигнала.
19. Перечислите основные свойства дискретного преобразования Фурье.
Линейность. Преобразование Фурье линейной комбинации функций будет такой же линейной комбинацией результатов преобразований Фурье этих функций по отдельности. Это свойство позволяет сводить сложные функции и их спектры к более простым. Если взять функцию, состоящую из суммы множества гармонических сигналов с разными частотами, то согласно свойству линейности, амплитудный спектр этой функции будет состоять из соответствующего набора дельта-функций.
Задержка. Это независимость амплитудного спектра от сдвига сигнала по времени. Если мы сдвинем функцию влево или вправо по оси t, то поменяется лишь её фазовый спектр.
Растяжение (сжатие). Это возможность растяжения (сжатия) исходной функции по оси времени. Растяжение исходной функции по оси t пропорционально сжимает её амплитудный спектр по оси частот (f). И наоборот сжатие исходной функции по оси t пропорционально растягивает её амплитудный спектр по оси частот (f).
Свертка функций. Это возможность свести свертку функций к поточечному перемножению их Фурье-образов. Данное свойство служит основой для алгоритмов линейной цифровой фильтрации.
Поточечное перемножение. Это возможность свести поточечное перемножение функций к свертке их Фурье-образов. Данное свойство используется для проектирования цифровых фильтров.
Симметрия. Это симметрия амплитудного спектра вещественного сигнала. На практике большинство сигналов описываются действительными функциями. Амплитудный спектр действительнозначной
функции является четной функцией, а фазовый спектр (если его привести к диапазону от –π до π) – нечетной. По этой причине на графиках спектров часто не изображают отрицательную часть спектра, т. е. рисуют физический спектр. Для действительнозначных сигналов часть спектра, соответствующая отрицательным частотам, не дает никакой новой информации.
Применение для сигналов, имеющих конечную энергию. Это применение преобразования Фурье к сигналам, имеющим конечную энергию. Преобразование Фурье осмысленно только для сигналов конечной продолжительности. Спектр таких сигналов должен быть отличным от нуля только на некотором конечном временном отрезке.
20. Что такое быстрое преобразование Фурье? При каких условиях
достигается наибольшее ускорение вычислений при выполнении алгоритма
быстрого преобразования Фурье?
БПФ – способ вычисления ДПФ, служащий для ускорения процесса вычисления ДПФ, который позволяет разделить общий процесс вычисления на части и далее объединить результаты вычислений отдельных частей. Однако у большинства алгоритмов БПФ есть особенность: они способны работать с максимальным быстродействием в тех случаях, когда количество отсчетов анализируемого сигнала является степенью двойки. Обычно это не представляет большой проблемы, так как анализируемый сигнал всегда можно дополнить нулями до необходимого размера. При выполнении БПФ может возникнуть «растекание» или «расширение» спектра анализируемого сигнала. Иными словами, при выполнении определенных условий амплитудный спектр, полученный в результате БПФ, может отличаться от теоретического. Если соотношение между частотой дискретизации и частотой гармонического сигнала таково, что в выборке содержится в точности целое число периодов, то «растекания» амплитудного спектра сигнала происходить не будет.
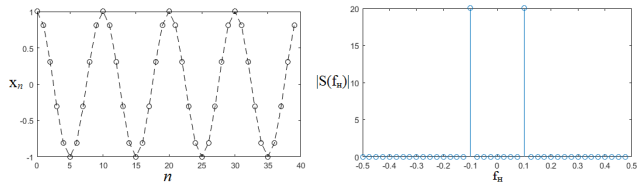
Примеры сигнала и соответствующего ему результата ДПФ представлены на рисунке;
Если же в выборке нет целого числа периодов, то спектр будет расширен вследствие появления дополнительных гармоник.
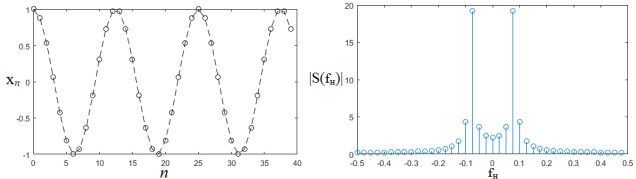
Примеры сигнала и соответствующего ему «расширенного» спектра показаны на рисунке.