Определение коэффициента гидравлического трения и потери энергии на трение по длине трубы.

Цель работы: На основании теоретических закономерностей и экспериментальных данных научиться определять коэффициент сопротивления трубы различных параметров и потери энергии на трения.

Теоретическая часть.

Потеря напора (удельная энергия жидкости) называется гидравлическими потерями жидкости. Гидравлические потери зависят от формы, размеров и шероховатости русла, а также от скорости жидкости и ее вязкости.

Гидравлические потери делятся на два вида: местные потери и потери на трение по длине Местные потери возникают в местных гидравлических сопротивлениях. Это различного рода изменения направлений или конфигурации потока (расширения, сужения, повороты различные препятствия (кроме задвижки)). Потери на трение возникают в прямых трубах постоянного сечения и возрастают пропорционально длине. Причина этих потерь – внутреннее трение жидкости, поэтому они могут наблюдаться не только в шероховатых, но и в гладких трубах. Определяется по формуле:



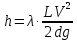
где 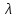– коэффициент сопротивления трубы;

L - длина;

d - диаметр;

V - скорость;

g – ускорение свободного падения.



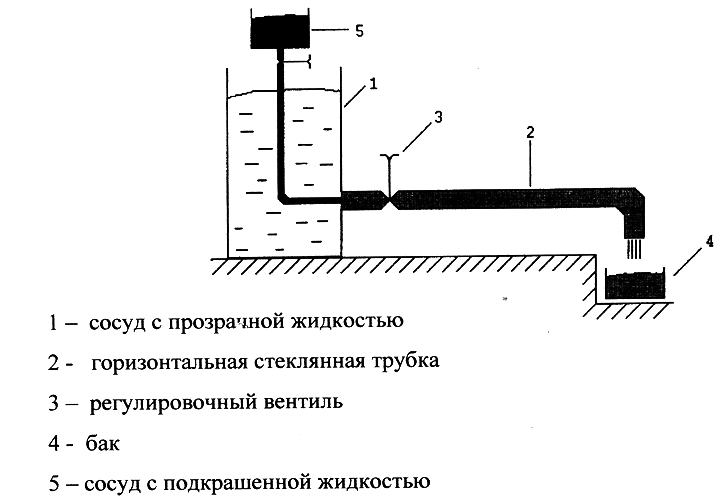
При малых скоростях течение жидкости окрашенная жидкости, подаваемая в трубу 2, двигается в виде тонкой струйки, не смешиваясь с потоком прозрачной жидкости. При увеличении скорости, струйка начинает колебаться, а ее очертания принимают волнообразный характер. При дальнейшем увеличении скорости очертания струйки размываются, а в отдельных местах появляются разрывы. Наконец при определении скорости подкрашенная струйка полностью размывается, при чем частицы красящих веществ равномерно окрашивают всю жидкости в трубе 2.

Режим движения при малых скоростях, при котором отдельные частицы движутся параллельно друг другу, не перемешиваются, называется ламинарным.

Режим движения при больших скоростях, при котором нет определенной закономерности, а траектории частиц пересекаются и движутся по сложным траекториям, называется турбулентным. Основным фактором для определения режима движения жидкости,

---

является критерий Рейнольдса, определяется по формуле



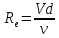
Число Рейнольдса, при котором происходит переход от ламинарного движения к турбулентному, называется критическим,

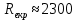
Таблица 1 – Исходные данные

Наименование	1	2	3	4	5	6
Длина L, см	50	70	90	120	140	160
Диаметр d, см	10	12	15	25	40	60
Объем вытекающей жидкости W, см3	2000	4000	6000	8000	10000	12000
Время наполнения бака Т, с	35	45	50	60	70	80
Коэффициент киниматической вязкости v, см2/с	0,00182

Порядок выполнения работы

1. 
   Вычисляем расход жидкости по формуле: ,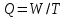
   

где: W – объем жидкости,

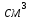
Т – время наполнения бака, с

2. 
   Вычисляем среднюю скорость истечения жидкости: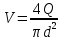
   

где: Q – расход жидкости,

---

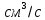
d – диаметр трубы, см

3. 
   Определяем число Рейнольдса
   

где: V – скорость истечения жидкости, см/с

d – диаметр трубы, см

4. 
   Вычисляем коэффициент сопротивления трубы в зависимости от числа Рейнольдса:
   

для ламинарного движения



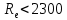
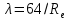
для турбулентного движения: если



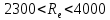
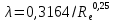
для турбулентного движения: если



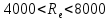
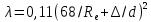
где: 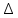- шероховатость поверхности = 1,5 мм

d – диаметр трубы, см

5. 
   Вычисляем потери энергии по длине трубы: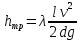
   

где: – коэффициент сопротивления трубы, см

l – длина трубы, см

V – скорость истечения жидкости, см/с

d – диаметр трубы, см

g – ускорение свободного падения,

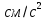
Полученные данные

Наименование	1,00	2,00	3,00	4,00	5,00	6,00
Расход жидкости Q,	57,14	88,89	120,00	133,33	142,86	150,00
Средняя скорость истечения жидкости V, см/с	0,73	0,79	0,68	0,27	0,11	0,05
Число РейнольдсаRe	3999,6	5184,7	5599,5	3733,0	2499,7	1749,8
Коэффициент сопротивления	0,04	0,07	0,06	0,04	0,04	0,04
Потери энергии,	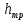5,37E-03	1,23E-02	8,99E-03	7,31E-04	1,03E-04	1,40E-05

---

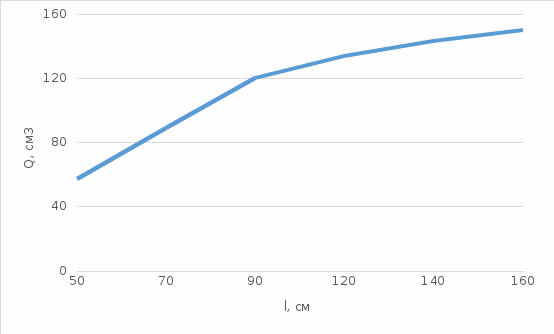
Расход жидкости от длины трубы Q = f (L)

Контрольные вопросы-ответы:

1. 
   Зависимость режима движения жидкости от числа Рейнольдса?
   

Число Рейнольдса определяет границы, между которыми режим движения жидкости может принимать ламинарный или турбулентный характер.

2. 
   Критическое значение числа Рейнольдса?
   

Для каждого вида течения существует критическое число Рейнольдса, R_ecr, которое, как принято считать, определяет переход от ламинарного течения к турбулентному. При R_eecr течение происходит в ламинарном режиме, при R_e>R_ecr возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.). Например, для течения воды в круглой R_ecr

3. 
   Режимы движения жидкости?
   

В зависимости от рода жидкости, скорости ее движения и характера стенок, ограничивающих поток, различают два основных режима движения: ламинарный и турбулентный. Ламинарным называют упорядоченное движение, когда отдельные слои скользят друг по другу, не перемешиваясь. Ламинарный режим движения можно наблюдать чаще у вязких жидкостей, таких как нефть, масла и т. п.

Турбулентным называют режим, при котором наблюдается беспорядочное движение, когда частицы жидкости движутся по сложным траекториям и слои жидкости постоянно перемешиваются друг с другом. Турбулентный режим движения можно наблюдать чаще у жидкостей, таких как вода, керосин и т. п.

4. 
   Характер движения жидкости при различных режимах движения?
   

Ламинарный режим – это Слоевое или послойное движение жидкости. Ламинарный режим наблюдается при малых скоростях жидкости, при этом струйки движутся параллельно не перемешиваясь.



Турбулентный режим – это вихревой беспорядочный режим движения. Наблюдается при больших скоростях движения маловязких жидкостей. При турбулентном режиме струйки пересекаются друг с другом и жидкость полностью перемешивается. Однако при турбулентном движении у стенок трубопровода наблюдается ламинарный режим. Слой толщиной   называется ламинарным пограничным слоем. Распределение скоростей по сечению плавное и напоминает гиперболу.

5. 
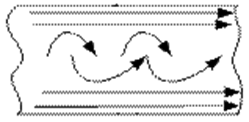
   Виды потерь? Причина возникновения потерь?
   

При течении реальной жидкости возникают силы сопротивления, обусловленные вязкими напряжениями. Эти силы производят работу, которая целиком превращается в тепловую энергию. Следовательно, при течении жидкости происходит процесс необратимого превращения части механической энергии во внутреннюю энергию. Работа сил вязкости, произведенная между двумя сечениями потока и отнесенная к единице веса движущейся жидкости, называется потерями напора hf .

• 
  Потери напора на трение, или потери по длине, возникают в чистом виде в прямых трубах постоянного сечения, т. е. при равномерном течении жидкости. 
  
• 
  Для грубой количественной оценки шероховатости используется понятие средней высоты выступов. Эта высота, измеряемая в линейных единицах, называется абсолютной шероховатостью и обозначается обычно буквой .
  

При одной и той же величине абсолютной шероховатости влияние ее на величину гидравлических сопротивлений различно в зависимости от диаметра трубы. Поэтому вводится понятие относительной шероховатости, измеряемой отношением абсолютной шероховатости к диаметру трубы.

Кроме того, даже при одной и той же абсолютной шероховатости и одинаковом диаметре трубы из разного материала могут иметь совершенно различное сопротивление в зависимости от формы выступов, густоты и характера их расположения и т. д. Учесть это влияние непосредственными измерениями практически невозможно.

В связи с этим в практику гидравлических расчетов было введено представление об эквивалентной разнозернистой шероховатости э. Под эквивалентной шероховатостью понимают такую высоту выступов шероховатости, сложенной из песчинок одинакового размера, которая дает одинаковую с заданной шероховатостью величину коэффициента гидравлического трения λ.

• 
  Коэффициент гидравлического трения
  

При ламинарном движении расчетная зависимость для λ может быть получена чисто теоретическим путем. Ввиду сложности турбулентного течения и трудности его теоретического исследования до сих пор не создано достаточно строгой и точной теории этого течения. Поэтому при турбулентном течении λ находится по различным эмпирическим формулам, предлагаемым разными авторами. Расчетные формулы для λ предусматривают зависимость этого коэффициента в общем случае только от шероховатости стенок русла и от числа Рейнольдса.

---

Смотрите также файлы

• Почему душа истинного философа бежит от радостей, желаний, печалей и страхов.docx

• По учебному курсу Организация, проведение оценки и аттестации персонала 1.docx

• Кирюшин 2эбф2 Tiktok Круглосуточные развлечения.docx

• Сж таырыбы Бала дамуындаы ауытуларды диагнозына сай оыту дісін дрыс тадау Орындаан Нарынбекова Д. Б. Тексерген Карменова К. А. Семей 2020 Бала дамуындаы ауытуларды диагнозына сай оыту дісін дрыс тадау.docx

• Российский государственный социальный университет Факультет дистанционного обучения практическое задание 1 по дисциплине Основы противодействия коррупции.docx