Файл: Тригонометрические функции.doc

Пользуясь значениями тригонометрической функции y=sinx из таблицы, построим график.

y


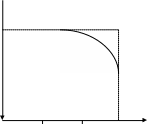
y=sinx

1

0 30° 60° 90° x

Рис.4.

Основные соотношения между тригонометрическими функциями острого угла

Для прямоугольного треугольника в соответствии с теоремой Пифагора

a²+b²=c²

и ли




По определению тогда




(1)

Легко также найти следующие зависимости




(2)

(3)




(4)




(5)

И з соотношений (1)-(5), которые называют основными, можно вывести и другие вспомогательные соотношения, например:

(6)

(7)

(8)

Соотношения (1)-(8) связывают все тригонометрические ф
ункции так, что по значению одной из них для данного острого угла можно найти значения всех остальных функций для этого же угла.

Тригонометрические функции произвольного угла

П усть в прямоугольной системе координат x0y задан радиус-вектор образующий с положительным направлением оси 0x угол a. Будем считать, что ось 0x — начальная сторона, а вектор - конечная сторона угла a. Проекция вектора на координатные оси соответственно обозначим

---

a_x и a_y.

М ожно показать, что отношения где а — длина вектора , зависят только от

в еличины угла a и не зависят от длины вектора . Поэтому эти отношения можно рассматривать как функции произвольного угла a.

Синусом угла a,образованного осью 0x и произвольным радиусом-вектором , называется отношение проекции этого вектора на ось 0y к его длине:




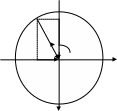y

A

a_y





a_x 0
x

Рис. 6.

Е сли не указано сколько оборотов совершил вектор вокруг точки 0, то положение вектора определяет угол с точностью до целого оборота, т.е углу с начальной стороной 0x и конечной стороной соответствует бесчисленное множество углов, которые выражаются формулой

360°·n+a, где n=0; ±1; ±2; 3; ±4; …

и sin(a+360°· n)=sina

Длина радиуса-вектора всегда число положительное. Проекция его на координатные оси величины алгебраические и в зависимости от координатных четвертей имеют следующие знаки:

В I четверти a_x>0; a_y>0;

Во II четверти a_x<0; a_y>0;

В III четверти a_x<0; a_y <0;

В IV четверти a_x>0; a_y<0/

График функции y=sinx

До сих пор аргументами тригонометрических функций рассматривались именованные величины — углы (дуги), измеренные в градусах или радианах. Значения тригонометрических функций, как отношения отрезков, являются абстрактными величинами (числами). При изучении свойств тригонометрических функций приходится сравнивать изменения функции в связи с изменениями аргумента, а сравнивать можно только однородные или

---

, что еще лучше, абстрактные величины.

Кроме того, введение тригонометрических функций от абстрактного аргумента дает возможность применять эти функции в различных вопросах математики, физики, техники и т.д.

В место именованного значения аргумента тригонометрических функций в x (радианов) будем рассматривать абстрактное число где r обозначает радианы, ии по определению принять что

sinx, где x — абстрактное число, равен sinx, где x измерен в радианах.

Тригонометрические функции являются периодическими, то есть существует число а, отличное от 0, такое, что при любом целом nтождественно выполняется равенство:

f(x+na)=f(x), n=0; ±1; ±2 ...

Число а называется периодом функции. Период функции sinx равен 2p. Для нее имеет место формула:

sin(x+2pn)= sinx, где n=0; ±1; ±2 ...

График функции y=sinx называют синусоидой. Для построения графика можно взять значения аргумента x с определенным интервалом и составить таблицу значений y=sinx, соответствующих выбранным значениям x, а затем по точкам, как это часто делается в алгебре, построить график.

С троим в системе координат x₁0₁y₁ единичную окружность R=1 с центром 0₁ на оси абсцисс x₁. Дугу этой окружности начиная от точки начиная от точки оси абсцисс x₁ =+1, делим на n равных частей:

З 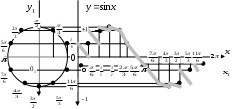атем строим вторую систему координат x0y, ось которой 0x совпадает с осью 0₁ x₁ , но сначало координат 0₁(x₁ =0) и 0(x=0) у етих систем различные. В новой системе координат отрезок оси абсцисс от x=0 до x=2p делим на n равных частей: Из точек деления окружности проводим прямые параллельные оси 0x, а из точек деления отрезка [0, 2p] проводим прямые, перпендикулярные этой осм. Точки пересечения соответствующих прямых будут точками графика y=sinx, так как ординаты этихточек равны значениям синуса, соответствующим значениям аргумента в точках деления отрезка [

---

0, 2p].

Рис.8.

Некоторые свойства функции y=sinx

1. Непрерывность.

Функция y=sinx существует при всех действительных значения x, причем, график ее является сплошной кривой линией (без разрывов), т.е. функция sinx непрерывна.

2. Четность, нечетность.

Функция y=sinx нечетная и ее график симметричный относительно начала координат.

3. Наибольшие и наименьшие значения.

Все возможные значения функции sinx ограничены неравенствами

- 1£ sinx £+1,

причем sinx=+1, если




и sinx=-1, если

4.Нулевые значения (точки пересечения графика функции с осью абсцисс).

sinx=0, если x=n (n=0; ±1; ±2;…).

5. Интервалы возрастания и убывания.

Функция возрастает, т.е. большему значению аргумента соответствует большее значение функции на интервалах




(n=0; ±1; ±2;…).

И убывает, т.е. большему значению аргумента соответствует меньшее значение функции на интервалах




(n=0; ±1; ±2;…).

---