Файл: Динамическая линейная сочимодель распределения ресурсов в маркетинговых сетях безразличный Центр.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 33
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Динамическая линейная СОЧИ-модель распределения ресурсов в маркетинговых сетях: безразличный Центр
АННОТАЦИЯ. В статье рассматривается динамическая модель сочетания общих и частных интересов распределения ресурсов в маркетинговых сетях. В качестве общих интересов агента влияния рассматривается общее для маркетинговой сети дело – привлечение клиентов (базовых агентов), создание хорошего мнения клиентов о товаре, распространяемом в соцсети агентами влияния. В качестве функций частной деятельности брались линейные функции Доказано, что ценность базового агента для всех агентов влияния и для Центра одинакова и зависит только от его связей. Различаем Центр благожелательный и безразличный к частным интересам базового агента. В данной статье рассматривается случай безразличного Центра. Доказано, что базовый агент тратит на повышение заинтересованности агента влияния меньше средств, чем считает нужным Центр.
Ключевые слова: СОЧИ-модель, базовые агенты, агенты влияния, благожелательный Центр, безразличный Центр
Введение
Модель, рассматриваемая в статье, основана на модели обмена мнениями и динамической модели сочетания общих и частных интересов (СОЧИ-модели).
В модели сочетания общих и частных интересов [1] имеется несколько агентов. В основном, рассматриваются равноправные агенты, но в некоторых разновидностях модели агенты могут быть связаны иерархическими соотношениями. Агенты объединены одной общей целью, которая требует вложения ресурсов с их стороны. Но кроме этой общей цели каждый агент имеет свою частную цель, которая также требует вложений ресурсов со стороны агента. Перед агентом стоит задача распределить имеющиеся у него ресурсы между общими и частными интересами.
Если общие и частные цели требуют одноразового вложения средств, то рассматривается статическая СОЧИ-модель, в противном случае образуется динамическая СОЧИ-модель. На базе динамической СОЧИ-модели и неоклассической социо-эколого-экономической модели Солоу построена модель трансграничного взаимодействия регионов в составе макрорегиона [4].
В моделях обмена мнениями [2] имеются агенты влияния, которые распространяют информацию о товары между базовыми агентами целевой аудитории. Считается, что на мнение агента целевой аудитории может воздействовать не только агент влияния, но и такие же базовые агенты, к мнению которых он прислушивается. Целью агента влияния является максимально хорошее о товаре суммарное мнение всех базовых агентов.
В статье [3] рассматривается распределение ресурсов в маркетинговых сетях, основанных на динамической модели обмена мнениями. Авторы данной статьи решили пойти дальше и ввели в целевую функцию агентов влияния слагаемое, представляющее его частные интересы.
Далее, структура статьи следующая. В п.2 приводится математическая модель сочетания общих и частных интересов при распределении ресурсов в маркетинговых сетях. В п.3 уточняется специфика рассматриваемой модели и перечислены используемые для ее исследования методы. В п.4 находится равновесие по Нэшу в игре базовых агентов. В п.5 и в п.6. находятся Парето-оптимальные решения в случае безразличного и благожелательного Центров соответственно. В п.7 приводятся выводы.
Математическая модель
На основе моделей обмена мнениями и моделей сочетания общих и частных интересов построим динамическую модель сочетания общих и частных интересов (далее, СОЧИ-модель) распределения ресурсов в маркетинговых сетях:
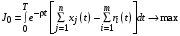 , (1)
, (1)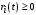 ,
, 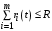 ,
, 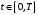 ,
, 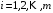 , (2)
, (2)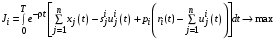 , (3)
, (3)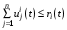 ,
, 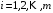 ,
, 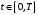 , (4)
, (4)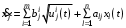 ,
, 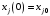 ,
, 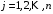 , (5)
, (5)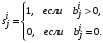 (6)
(6)(1)-(6) – дифференциальная иерархическая игра. Здесь n – число базовых агентов (численность целевой аудитории), m – число агентов влияния (конкурирующих субъектов маркетинга), при этом, поскольку разные фирмы по-разному решают вопрос, на каких агентов сильных подгрупп влиять, а на каких – нет, мы просто считаем, что если i-ая фирма не влияет на j-го агента, то
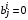 .R – общий маркетинговый бюджет Центра, T – период рассмотрения (длина игры),
.R – общий маркетинговый бюджет Центра, T – период рассмотрения (длина игры), 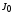
,
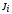 – функционалы выигрыша Центра и агентов влияния соответственно,
– функционалы выигрыша Центра и агентов влияния соответственно, 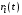 – маркетинговый бюджет, выделяемый Центром i-му агенту в момент t,
– маркетинговый бюджет, выделяемый Центром i-му агенту в момент t, 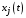 – мнение j-го базового агента в момент t,
– мнение j-го базового агента в момент t, 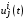 – расходы i-го агента влияния на маркетинговое воздействие на j-го базового агента в момент t,
– расходы i-го агента влияния на маркетинговое воздействие на j-го базового агента в момент t, 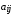 – коэффициент влияния i-го базового агента на j-го,
– коэффициент влияния i-го базового агента на j-го, 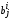 – коэффициент воздействия i-го агента влияния на j-го базового агента.
– коэффициент воздействия i-го агента влияния на j-го базового агента.В качестве общих интересов в модели принимается максимизация мнения всех базовых агентов системы.
Допущения модели, цель и методы исследования
Динамическими СОЧИ-моделями распределения ресурсов в сетевом маркетинге мы стали заниматься совсем недавно. На сегодняшний момент рассмотрен самый простой случай – случай линейных функций частного дохода базовых агентов, т.е.
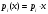 .
.Различаем Центр благожелательный и безразличный к частным интересам базового агента. В случае благожелательного Центра в его целевую функцию Ведущего включаются частные интересы агентов влияния. В этом случае функция Ведущего представляет собой функцию общественного благосостояния, в которой суммируются целевые функции всех агентов влияния, в каждой из которых сочетаются общие и частные интересы последнего за минусом затрат ресурсов на достижение своих целей.
В случае же Центра, безразличного к частным интересам агента, последние не входят в целевую функцию Центра, которая представляет собой только максимизация суммарного мнения всех базовых агентов за минусом ресурсов, выделяемых им i-й фирме на привлечение клиентов. В данной статье рассмотрен лишь безразличный Центр.
В статье найдены единственные равновесия по Нэшу и Парето-оптимальное решение, для нахождения которых применялся метод Гамильтона-Якоби-Беллмана.
Полученные результаты планируется распространить на случай степенной вогнутой функции частного дохода, а также на случай произвольной производственной функции.
Нахождение равновесия по Нэшу.
Исследуем задачу i-ой фирмы (3)-(6).
Выпишем уравнение Гамильтона-Якоби-Беллмана:
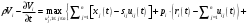
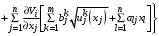
при условии
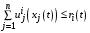 .
. Максимизируя по
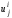 ,
,  ,
, 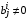 , получаем
, получаем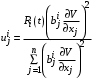 . (2)
. (2)где
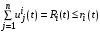 .
.Поскольку функции Беллмана в нашей ситуации мы считаем линейными,
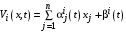 ,
,можем записать уравнение (1) с учетом (2) в виде
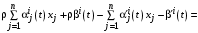
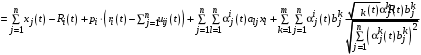 . (3)
. (3)Приравнивая в левой и правой частях уравнения (8) коэффициенты при первых степенях x, получаем следующие дифференциальные уравнения для коэффициентов
 :
: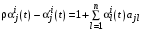 ,, (4)
,, (4)здесь
 .
. Перепишем систему уравнений (4) в матричной форме
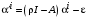 , (5)
, (5)где
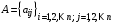 – матрица влияний,
– матрица влияний, 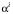 – вектор-столбец коэффициентов
– вектор-столбец коэффициентов 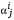 ,
,  , I – единичная матрица,
, I – единичная матрица,  – n-мерный столбец единиц.Мы видим, что система уравнений (5) одна и та же у всех агентов влияния, поэтому
– n-мерный столбец единиц.Мы видим, что система уравнений (5) одна и та же у всех агентов влияния, поэтому 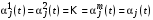 для любого базового агента
для любого базового агента  , и с этого момента мы будем опускать индекс i у коэффициентов
, и с этого момента мы будем опускать индекс i у коэффициентов 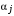 .
.Решая систему дифференциальных уравнений (4), получаем:
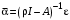 ,
,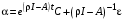
.
Вектор-столбец постоянных интегрирования найдем из граничных условий:
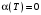 ,
,поэтому
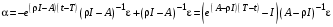 .
.В частности, при
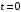 имеем
имеем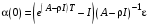 . (6)
. (6)Далее, учитывая, что
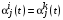 для любого
для любого 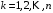 , перепишем (3) в виде:
, перепишем (3) в виде:
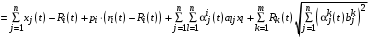 .Выбирая максимальное значение величины правой части выражения (1) в зависимости от суммы
.Выбирая максимальное значение величины правой части выражения (1) в зависимости от суммы 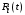 , имеем
, имеем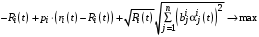 ,
,откуда
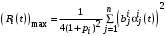 .
.Значит, величина
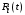 в (12) равна
в (12) равна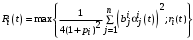 . .
. .Заметим, что условие
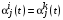 означает, что ценность каждого базового агента одинакова для всех агентов влияния, и, судя по (6), зависит только от его коэффициентов
означает, что ценность каждого базового агента одинакова для всех агентов влияния, и, судя по (6), зависит только от его коэффициентов 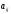 , т.е. только от его связей с другими агентами, а значит и влияния на других агентов.
, т.е. только от его связей с другими агентами, а значит и влияния на других агентов.Приравнивая свободные члены в левой и правой частях уравнения (7), получаем дифференциальное уравнение для
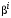 :
: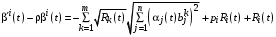 . (8)
. (8)Уравнение (13) решаем методом вариации произвольных постоянных:
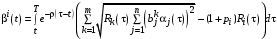 .
.При
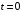 имеем
имеем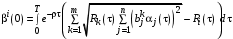 ,
, где для любого
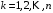 (в частности, для данного i), имеем
(в частности, для данного i), имеем