Добавлен: 06.11.2023
Просмотров: 39
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Содержание
Введение…………………………………………………………………………..
1. Исторические начала квантовой механики…………………………………..
2. Фундаментальные понятия квантовой механики……………………..…….
2.1 Гипотеза де Бройля……………………………………………………..……
2.2 Принцип неопределённостей Гейзенберга…………………………………..
2.3 Квантовое состояние, сцепленность………………………………….…….
3. Эксперимент над квантовомеханической системой…………………………
3.1 Особенности описания движения микрочастиц…………………..……….
4. Парадоксы квантовой теории…………………………………………………
4.1 Парадокс ЭПР…………………………………………………………………
4.2 Редукция фон Неймана. Кот Шрёдингера……………………….…………
Заключение………………………………………………….……………………
Список литературы……………………………………………………………….
Введение
Проблема измерения актуальна для любой физической теории. В квантовой механике она сопровождалась актуальным проблемным обсуждением. Это объясняется резким отличием классического и квантово-механического понимания феномена измерения. Эта проблема всегда присутствовала в квантовой теории, но никогда не мешала ей развиваться и описывать микромир с изумительной точностью.
В классической механике измерение понимается как фиксация значений некоторых параметров, которые существуют до процесса измерения. Понимание процесса измерения при этом, как правило, не сопрягается с основаниями теории, в частности с ее принципами.
А в релятивистской механике измерение осмысливается именно в контексте ее принципов. В результате вся проблема измерения предстала в новом свете, насыщенном концептуальными тонкостями. Именно это обстоятельство вызвало наибольшее удивление. И в специальной теории относительности, и в теории тяготения процесс измерения понимается динамически, что также немаловажно. Именно в процессе измерения волновая функция проявляет свою вероятностную природу, и проявляется необратимость, свойственная квантовой механике. Состояние системы меняется скачком, и после измерения мы с некоторыми вероятностями имеем разные волновые функции и различные результаты измерения.
Поскольку данный процесс существенно нелокален, а из мгновенности изменения следует распространение взаимодействий быстрее скорости света, то считается, что он является не физическим процессом, а математическим приёмом описания.
Волновая функция аналогична распределению вероятностей, и подобно ему задает вероятность всех возможных исходов измерения некоторого ¨ набора величин, полностью задающего состояние системы. То есть если все эти величины определены, то состояние системы определяется однозначно. В классической механике других состояний систем и не бывает. В квантовой механике такие состояния образуют лишь базис в линейном пространстве состояний.
1. Исторические начала квантовой механики
квантовый механика микрочастица волновой
Считается, что квантовая физика, сыгравшая принципиально важную роль в развитии науки и техники, появилась в ХХ столетии. К этому времени классическая физика столкнулась с непреодолимыми трудностями при рассмотрении электромагнитного излучения нагретых тел.
Предположение о том, что изменение энергии излучения происходит непрерывно, привело к теоретическим результатам, противоречащим данным экспериментов в области коротковолнового диапазона излучения. В 1900 году решение этой проблемы предложил Макс Планк, выдвинув принципиально новую гипотезу о том, что энергия излучения осуществляется дискретными порциями – квантами. Основанная на этой гипотезе квантовая теория излучения позволила Планку непротиворечивым образом описать равновесное тепловое излучении во всем диапазоне длин волн. Вместе с тем, сам Планк рассматривал квантование не иначе, как математический прием решения задачи об испускании и поглощении.
Альберт Эйнштейн, развивая гипотезу о квантах, выдвинул корпускулярную теорию, в которой электромагнитное излучение не только порождается, но и существует с промежутках между поглощением и испусканием в виде потока квантов, названных фотонами (1905). Фотонная теория позволила объяснить явления квантовой оптики.
В 1924 году Луи де Бройль выдвинул радикальную гипотезу о волновом характере материи. Он предположил, что электромагнитные волны (фотоны) могут вести себя как частицы, а частицы – как волны. Такая двойственность, получившая название корпускулярно-волнового дуализма, приводит к существенным отличиям в описании движения микрочастиц в квантовой механике по сравнению с классической механикой. В частности, Дж. фон Нейман попытался сблизить квантовую теорию с классической механикой, и составил уравнение, дающее математическое описание материи с помощью терминов волновой функции. Так возникла волновая механика.
Незадолго до этого Вернер Гейзенберг, Макс Борн и Паскуаль Иордан опубликовали вариант квантовой теории, получивший название матричной механики, которая описывала квантовые явления с помощью таблиц наблюдаемых величин. Эти таблицы представляют собой определенным образом упорядоченные математические множества, называемые матрицами, над которыми по известным правилам можно производить различные математические операции. Матричная механика позволяла достичь согласия с наблюдаемыми экспериментальными данными, но в отличие от волновой механики не содержала никаких конкретных ссылок на пространственные координаты или время. Согласно доказательству Шрёдингера, волновая механика и матричная механика математически эквивалентны. Окончательное формирование квантовой механики как последовательной теории связано с работой Вернера Гейзенберга 1927 года, в которой был сформулирован принцип, утверждающий, что любая физическая система не может находиться в состояниях, в которых координаты ее центра инерции и импульс одновременно принимают вполне определенные, точные значения. Этот принцип получил название "соотношение неопределённостей". Известные ныне под общим названием квантовой механики, вышеперечисленные достижения дали долгожданную общую основу описания квантовых явлений.
2. Фундаментальные понятия квантовой механики
2.1 Гипотеза де Бройля
И волновые, и корпускулярные свойства частиц нашли очень широкое применение при изучении различных физических явлений. В 1924 г. Луи де Бройль выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. По гипотезе де Бройля каждая материальная частица обладает волновыми свойствами, причем соотношения, связывающие волновые и корпускулярные характеристики частицы, остаются такими же, как и в случае электромагнитного излучения. Таким образом, если частица имеет энергию E и импульс, абсолютное значение которого равно p, то с ней связана волна, распространяющаяся в том же направлении, что и частица, и описывающая ее волновые свойства. Частота этой волны описывается формулой:
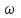= E / 
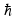,а её длина:
λ =
/ 
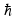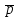,где
- постоянная Планка. Эта волна и получила название волны де Бройля.Соотношения, связывающие корпускулярные и волновые свойства частицы,
E =
, 
= 
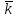
где
- это импульс частица, а 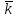- волновое число, получили название уравнений де Бройля.Экспериментальным подтверждением гипотезы де Бройля послужили экспериментальные исследования дифракции электронов на кристаллической решетке. Следует отметить, что т.к. длина волны де Бройля электрона имеет порядок, совпадающий с порядком расстояния между атомными плоскостями в кристалле (около 10-10 м), кристалл может играть роль дифракционной решетки для электронных волн. Наиболее значительными оказались экспериментальные результаты, полученные в ходе исследования дифракции электронов на совершенном кристалле (кристалле, обладающем идеальной кристаллической решеткой). Они показали состоятельность условия Вульфа-Брэгга, а именно появление дифракционного максимума тогда, когда разность хода волн, отраженных от соседних атомных плоскостей, равна целому числу длин волн де Бройля. Именно в этом случае волны усиливают друг друга, т.е. имеет место конструктивная интерференция.
2.2 Принцип неопределённостей Гейзенберга
Открытие волновых свойств у микрочастиц показывает, что в физике микромира мы имеем дело с принципиально новым объектом исследований. Отличие микрочастицы от волны состоит в том, что волну, используя, например, зеркало, можно разделить на две части и отдельно исследовать каждую из них. Микрочастица же, например, электрон или нейтрон, во всех опытах проявляется как единое целое. Никому еще не удавалось наблюдать пол-электрона или четверть нейтрона, и т.д.
Важное отличие квантовой механики от остальных теорий состоит в том, что в классических теориях описываются свойства объектов вне их отношения к тем приборам, с помощью которых обнаруживаются эти свойства, в то время как в квантовой механике учет условий наблюдения неотъемлем от самой теоретической постановки проблемы (при этом в различных макроскопических ситуациях микроявления обнаруживают различные, порой прямо противоположные свойства, например, частицы или волны). Вследствие этого мы имеем право говорить об изменении понятия наблюдения за микрочастицей. Действительно, наблюдение - это процесс взаимодействия объекта с прибором, в результате которого на выходе прибора появляется какой-то определённый сигнал. Но всякое взаимодействие, а значит, и просто наблюдение, само по себе возмущает наблюдаемый объект, изменяет его свойства. И важно, что это возмущение нельзя сделать пренебрежимо малым. Итак, при измерении какого-либо свойства частицы, и даже просто при её наблюдении, исходное состояние частицы, как правило, разрушается. Можно сказать, что какое-либо определённое квантовое состояние частицы – невероятно «хрупкая» вещь. Это важное свойство можно проследить на примере эксперимента под названием Which Way (Который путь).
В 1998 г. такой эксперимент был проведен с пучком атомов, которые последовательно пересекали систему из двух стоячих световых волн. Стоячие волны играли роль интерференционных решеток, после прохождения которых атомный пучок расщеплялся на четыре когерентных пучка. Эти пучки интерферировали между собой. С помощью дополнительных устройств, представляющих собой резонаторы с лазерным излучением, можно было получить информацию о пути атомного пучка до и после прохождения им световой решетки. Опыт показал, что при включении резонаторов интерференционная картина исчезала, а при выключении – вновь появлялась. Частицы будто бы чувствовали, что за ней наблюдают. Явление исчезновения интерференции при включении дополнительных приборов наблюдения получило название декогеренции. Важно, что декогеренция может наблюдаться даже в том случае, когда наблюдение не организуется намеренно, а является результатом взаимодействия частицы с ее окружением.
Таким образом, понятие траектории становится неприменимым по отношению к квантовой частице. Рассмотрим в качестве примера дифракцию электронов на щели. Пусть электроны падают нормально на непрозрачный экран, в котором имеется щель (рис. 1)
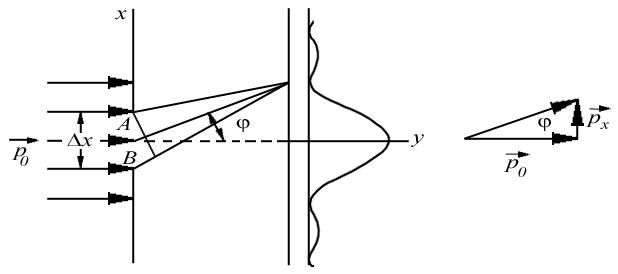
Рис. 1 - Картина дифракции электронов на щели
Дифракционная картина фиксируется фотопластинкой, расположенной за экраном. Пусть падающие электроны обладают определенным импульсом p. Тогда, согласно квантово-механическим представлениям, этим электронам соответствует плоская волна с волновым вектором
, определяемым из уравнений де Бройля. Поскольку волна распределена по всему пространству, каждый электрон до прохождения через щель имеет точно определенный импульс и неопределенную координату x. При прохождении электрона через щель ситуация меняется. Неопределенность координаты x становится равной ширине щели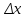 
, но при этом появляется неопределенность проекции импульса 
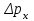, обусловленная дифракцией электронов на щели. Дело в том, что электроны, прошедшие через щель на экране, описываются уже не плоской, а расходящейся волной, интенсивность которой зависит от угла дифракции. Мы приходим к выводу: если мы пытаемся насильно избавить электрон от неопределённости в координате, то мы неизбежно увеличиваем неопределённость в импульсе электрона. То есть невозможно одновременно одинаково точно измерить координату и импульс частицы, а произведение двух неопределённостей никогда не бывает меньше конкретной величины, постоянной Планка. Это соотношение называется соотношением неопределённостей, а общий принцип носит название принципа неопределённостей Гейзенберга.