Добавлен: 06.11.2023
Просмотров: 40
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Закон имеет вид:
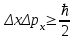 ,
,И его словесная формулировка такова: Улучшая наше знание о какой-либо одной характеристике частицы, мы ухудшаем наше знание о дополнительных её характеристиках. Наш эксперимент над электроном продемонстрировал неустранимое «квантовое дрожание» (обычно говорят: нулевые колебания) локализованной микроскопической частицы, и именно оно приводит к некоторым чисто квантовым явлениям.
Например, даже при нулевой температуре, когда, согласно классической механике, никакого движения не должно быть, нулевые колебания по-прежнему остаются. Именно из-за этого жидкий гелий не затвердевает при нормальном давлении даже при нулевой температуре. При всем этом нужно понимать, что неопределённость в измерениях связана не с несовершенством измерительной техники, а с объективными свойствами микромира. Очевидным также является то, что квантовая механика носит принципиально вероятностный характер и оперирует статистическими величинами, то есть далеко уходит от детерминированной методологии классической механики.
2.3 Квантовое состояние, сцепленность
Проблемы квантовых измерений влекут за собой ряд феноменов квантовой теории, которые следуют из необычных свойств изучаемых частиц. Квантовой сцепленностью называется квантовомеханическое явление, при котором квантовое состояние двух или большего числа объектов должно описываться во взаимосвязи друг с другом, даже если отдельные объекты разнесены в пространстве. Вследствие этого возникают корреляции (т.е. зависимость) между наблюдаемыми физическими свойствами объектов. Иными словами, измерения, проводимые над одной системой, оказывают мгновенное воздействие на сцепленную с ней. Однако то, что понимается под информацией в классическом смысле, не может быть передано через сцепленность из-за статистического характера передаваемой информации. Любопытным продолжением развития принципа неопределённости является квантовая криптография, а именно метод защиты коммуникаций, основанный на квантовых явлениях. Используя их, можно спроектировать и создать такую систему связи, которая всегда может обнаруживать подслушивание. Это обеспечивается тем, что попытка измерения взаимосвязанных параметров в квантовой системе вносит в неё нарушения, разрушая исходные сигналы, а значит, по уровню шума в канале легитимные пользователи могут распознать степень активности перехватчика.
3. Эксперимент над квантовомеханической системой
3.1 Особенности описания движения микрочастиц
Хорошо исследованный аппарат классической аналитической механики не подходит для описания движения микрочастиц, поскольку частицы в квантовой механике обладают как корпускулярными, так и волновыми свойствами. Микрочастицами принято считать частицы, длина волны де Бройля, которых сравнима или больше характерного размера области движения, поэтому в квантовой механике речь идет о микрочастицах.
В классической механике полный набор обобщенных координат и импульсов характеризует состояние механической системы. Изменение механического состояния во времени приводит нас к понятию траектории. Однако в квантовой механике координата и импульс подчиняются каноническому коммутационному соотношению. Отсутствие возможности задать состояние микрочастицы классическим образом привело исследователей к парадоксальному заключению об отсутствии траектории движения микрочастиц.
Волновая формулировка квантовой механики Шредингера позволяет описывать квантово-механическое состояние при помощи комплексной волновой функции. В 1926 году было выведено уравнение, описывающее пространственно-временное изменение состояния, заданного волновой функцией. Такое уравнение можно назвать нерелятивистским уравнением движения для микрочастицы. Уравнение Шредингера играет в квантовой механике такую же важную роль, как уравнение второго закона Ньютона в классической механике.
Уравнение Шредингера нашло применение для решения широкого круга задач квантовой механики. Например, результаты расчёта Н. Бора для частот и основных значений энергии при исследовании атома водорода были подтверждены в 1925-1926 гг. полным квантово-механическим анализом, с использованием уравнения Шредингера. Решение уравнения Шрёдингера для электрона в электростатическом поле атомного ядра может быть найдено в аналитической форме. Из него получают уровни энергии электрона и, таким образом, его частоты. Решение уравнения Шрёдингера даёт больше информации и о форме атомных орбиталей (их анизотропии) атома водорода.
Также при помощи уравнения Шредингера решаются задачи о движении частиц в потенциальных ямах, задача о туннелировании.
Важно отметить, что из уравнения Шредингера можно предельным переходом получить уравнение Ньютона. В этом смысле квантовая механика при описании движения микрочастиц не требует полного отказа от классической механики, а лишь определяет ее границы.
Однако уравнение Шрёдингера предназначено для частиц без спина, движущихся со скоростями много меньшими скорости света. Поэтому для описания большинства наблюдаемых явлений потребовались некоторые обобщения уравнения Шредингера.
Первым из таких обобщений стало уравнение Клейна-Гордона-Фока, которое описывает быстро движущиеся частицы, имеющих массу (массу покоя). Оно строго применимо к описанию скалярных массивных полей. Может быть обобщено для частиц с целым и полуцелым спинами. Кроме прочего, ясно, что уравнение Клейна-Гордона-Фока является обобщением обычного волнового уравнения.
Однако уравнение Клейна-Гордона-Фока не удовлетворяет в полной мере экспериментально наблюдаемым явлением, поэтому для строгого описания движения релятивистских частиц с полуцелым спином применяется уравнение Дирака. Именно уравнение Дирака помогло объяснить спин, который приписывался электронам. На основе уравнения Дирака были найдены формулы для вероятностей рассеяния фотонов свободными электронами (комптон-эффекта) и излучения электрона при его торможении (тормозного излучения), получившие экспериментальное подтверждение. Последовательное релятивистское описание движения электрона даётся квантовой электродинамикой.
Кроме того, волновая функция может описывать только чистые состояния, поэтому для описания смешанных состояний квантовых систем была введена матрица плотности. Для матрицы плотности введены фундаментальные эволюционные уравнения:
Уравнение Гейзенберга
Уравнение фон Неймана
Уравнение Линдблада
3.2 Основные принципы проведения измерений
В квантовой механике измерение – это концепция, которая описывает возможность получения информации о состоянии системы путём проведения физического эксперимента.
Исходя из такой трактовки развивалась матричная формулировка квантовой механики, основанная на введенном Гейзенбергом понятии наблюдаемой физической величины. Поэтому результаты любого измерения в квантово-механических системах должны интерпретироваться как значение некоторой физической величины, которой ставится в соответствие оператор физической величины – наблюдаемой.
Результаты измерения – это собственные значения рассматриваемых операторов. Полный набор собственных значений называется спектром оператора. При рассмотрении модели идеализированного «абсолютно точного» измерения могут быть получены только лишь такие значения физической величины, которые принадлежат спектру соответствующего этой величине оператора, и никакие другие.
Характерным примером такой концепции является классический опыт Штерна-Герлаха. Собственными значениями оператора проекции спина частицы со спином 1/2 на произвольное направление являются только величины:
Поэтому в эксперименте Штерна-Герлаха пучок таких частиц разделится только на два пучка с положительной и отрицательной проекцией спина на направление градиента магнитного поля.
Поскольку квантовая механика – статистическая теория, обработка результатов измерений зачастую требует привлечения мощного аппарата теории вероятности.
Наиболее важным направлением в экспериментальном исследовании квантовых систем являются ансамблевые измерения. Суть состоит в приготовлении и измерении большого числа частиц, находящихся в схожих квантовых состояний. Поскольку точность измерения напрямую зависит от количества приготовленных частиц, существует возможность проведения сверхточных экспериментов в квантовой механике.
4. Парадоксы квантовой теории
4.1 Парадокс ЭПР
В 1935 г. Эйнштейн, Подольский и Розен предложили мысленный эксперимент, из которого, по их мнению, следовало, что для описания физических объектов волновой функции недостаточно. Тем самым, утверждалось, что квантовая механика неполна. Эйнштейн, Подольский и Розен рассмотрели систему двух коррелированных частиц, т.е. таких частиц, свойства которых связаны, не будучи точно заданными. Например, частицы А и Б рождаются в одной точке, а затем разлетаются в разные стороны. В момент рождения ни у одной из них не заданы координата и импульс, но в силу закона сохранения импульса сумма их импульсов, как и сумма их координат, всегда равна нулю. Теперь, если мы проведем измерение над частицей А, например, измерим ее координату, то ее волновая функция "схлопнется" в соответствующей точке. Но в то же время "схлопнется" и волновая функция частицы Б, поскольку ее координата после такого измерения тоже станет известной точно. Если волновая функция полностью характеризует частицу, то значит, с частицей Б действительно что-то произойдет, а ведь измерение проводилось над частицей А, которая могла быть в этот момент очень далеко от частицы Б. А если изменится только волновая функция частицы Б, а сама частица останется точно такой же, значит, волновая функция - плохая характеристика квантовой частицы. В этом и заключается парадокс Эйнштейна-Подольского-Розена или, сокращенно, парадокс ЭПР.
Разрешение парадокса состоит в следующем. В действительности, рассуждение, предложенное Эйнштейном, Подольским и Розеном, нисколько не опровергает квантовую механику и даже концепцию волновой функции. Дело в том, что, как стало ясно уже после выхода статьи ЭПР, коррелированные частицы характеризуются лишь одной общей волновой функцией; каждой же из двух частиц определенную волновую функцию приписать нельзя. Поэтому в момент измерения над одной частицей действительно меняется как общая волновая функция обеих частиц, так и соответствующий квантовый объект - две коррелированные частицы.
Парадокс ЭПР имел большое значение для развития квантовой теории. Прежде всего, он стимулировал развитие ряда новых понятий и вызвал интерес к коррелированным состояниям квантовых частиц. Когда такие состояния были обнаружены экспериментально для фотонов, началось бурное развитие новой области в физике – квантовой оптики. Кроме того, эксперименты с коррелированными парами квантовых частиц (их также называют ЭПР-парами) позволили проверить, действительно ли вероятностное поведение характерно для отдельной квантовой частицы или это свойство совокупности частиц.
4.2 Редукция фон Неймана. Кот Шрёдингера
Для того, чтобы увидеть, как на самом деле изменяются параметры рассматриваемой квантовомеханической системы (например, электрон – прибор), нам понадобилась характеризующая ее волновая функция, или функция состояния. Когда мы начали измерять характеристику квантовой частицы, функция мгновенно изменилась. Этот эффект носит название редукции фон Неймана. В 1971 году Джон фон Нейман развил свою идею о том, что в каждом квантовомеханическом измерении наличествует неанализируемый элемент. Он постулировал, что волновая функция, помимо непрерывного изменения, при измерении претерпевает мгновенное изменение, обусловленное вмешательством наблюдателя, его воздействием на объект. С коллапсом волновой функции, а также неполнотой квантовой механики при переходе от субатомных систем к макроскопическим, непосредственно связан мысленный эксперимент, предложенный Эрвином Шрёдингером. Суть его такова:
В закрытый ящик помещён кот. В ящике имеется механизм, содержащий радиоактивное ядро и ёмкость с ядовитым газом. Параметры эксперимента подобраны так, что вероятность того, что ядро распадётся за 1 час, составляет 50 %. Если ядро распадается, оно приводит механизм в действие, он открывает ёмкость с газом, и кот умирает. Согласно квантовой механике, если над ядром не производится наблюдения, то его состояние описывается суперпозицией (смешением) двух состояний - распавшегося ядра и нераспавшегося ядра, следовательно, кот, сидящий в ящике, и жив, и мёртв одновременно. Если же ящик открыть, то экспериментатор может увидеть только какое-нибудь одно конкретное состояние - «ядро распалось, кот мёртв» или «ядро не распалось, кот жив».