Файл: Механические свойства жидкостей и газов.docx

Механические свойства жидкостей и газов.

Молекулы газа незначительно взаимодействуют (притягиваются на расстоянии) между собой, в этой связи они движутся почти свободно и занимают весь предоставленный объём.

Жидкость, имея определённый объём, принимает форму того сосуда, в который она помещена. Жидкость очень сложно сжать и для выведения различных соотношений в механике жидкостей вводится понятие идеальной жидкости.

Идеальная жидкость – абсолютно несжимаемая жидкость, в которой можно пренебречь трением слоёв друг о друга (вязкостью).

Жидкости и газы при взаимодействии с твёрдыми телами оказывают на них давление.

Давлением называется физическая величина, определяемая отношением модуля нормальной силы, действующей на некоторую поверхность к площади этой поверхности:



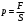
А саму эту силу называют силой давления.

Если на жидкость или газ оказывается давление, то она (он) передаёт это давление одинаково во всех направлениях. В этом заключается закон Паскаля.

Давление, производимое столбом жидкости или газа высотой 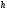, обусловлено действием на этот столб силы тяжести: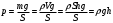

Для жидкости такое давление называется гидростатическим. Наличием этого давления обусловлено появление силы Архимеда, выталкивающей тело из жидкости или газа в которые оно погружено. Эта сила определяется по закону Архимеда:



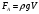
где 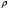- плотность жидкости, 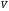- объём части тела, погруженной в эту жидкость.

Д вижение жидкости – течение, а совокупность частиц жидкости – поток. Изображать течение удобно при помощи линий тока – линий, касательные к которым совпадают по направлению с вектором скорости жидкости в данной точке пространства. Часть жидкости, ограниченная линиями тока, называется трубкой тока.

Если направление линий тока и значение скоростей жидкости в различных точках с течением времени не меняется, то течение называется установившимся или стационарным.

В трубке тока выберем два её сечения, с площадям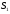и и 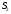. Т.к. течение стационарное, то за время 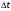через данные сечения пройдёт одинаковый объём жидкости: 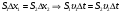или, сократив на 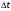, получим: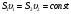



Это соотношение называется уравнением неразрывности.