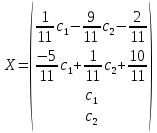Российский государственный социальный университет

РУБЕЖНЫЙ КОНТРОЛЬ 1по дисциплине «Математика»

ЛИНЕЙНАЯ АЛГЕБРА
ФИО студента Ярматов Ягшимурат Жумамуратович Направление подготовки Информационные системы и технологии в экономической сфере Группа ДО-ИСТ-Б-01-З-2022-А

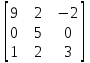
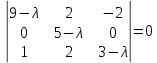
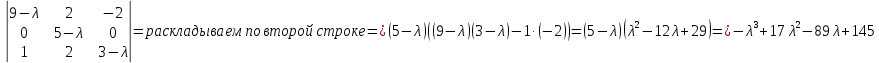
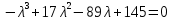
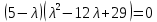
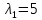
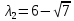
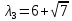
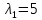
Москва 2023Рубежный контроль 1Линейная алгебраЗадача 1Определить собственные значения и собственные векторы матрицы третьего порядка. РешениеУравнение для нахождения собственных значений:Собственное значение:Найдем собственный вектор:

---

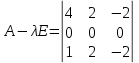
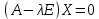
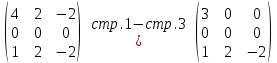
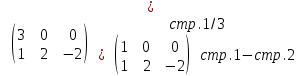
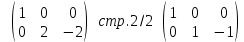
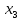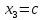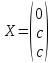
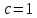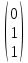
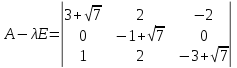
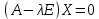
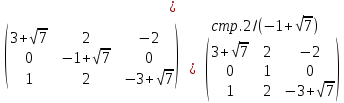
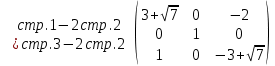
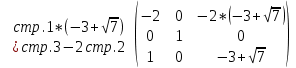
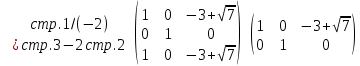
Тогда имеем однородную систему линейных уравнений, решим ее методом Гаусса:Полагая свободной - , получим следующее решение:Пусть , тогда собственный вектор:Собственное значение:Найдем собственный вектор:Тогда имеем однородную систему линейных уравнений, решим ее методом Гаусса:Полагая 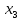свободной - 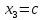, получим следующее решение: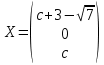Пусть 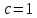, тогда собственный вектор: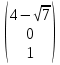Собственное значение:Найдем собственный вектор: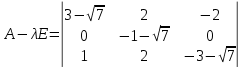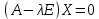Тогда имеем однородную систему линейных уравнений, решим ее методом Гаусса:

---

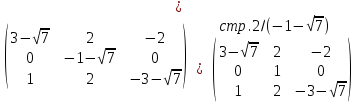
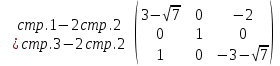
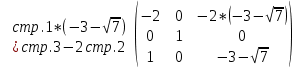
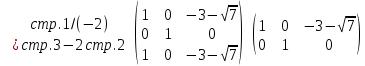
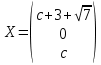
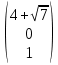
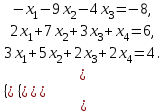
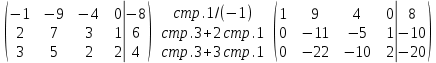
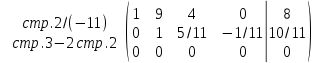
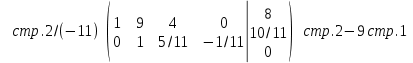
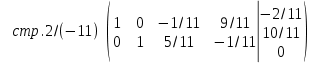
Полагая свободной - , получим следующее решение:Пусть , тогда собственный вектор:Задача 2Доказать совместность системы и решить её тремя способами: по формулам Крамера, методом Гаусса и средствами матричного исчисления.Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы.Вычислим ранг расширенной матрицы:Ранг расширенной матрицы равен рангу основной матрицы и равен 2.Количество переменных равно 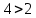, следовательно система имеет бесконечное значение решений. 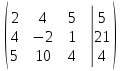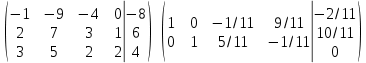Решение системы по формулам Крамера и средствами матричного исчисления не возможно.Метод ГауссаЗапишем расширенную матрицу системы: Получим единицы на главной диагонали.Полагаем 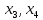свободными - 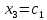, , 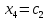получим следующее общее решение:

---

Смотрите также файлы

• Развивающие игры как средство обучения детей дошкольного возраста.doc

• Вредные привычки московской молодежи.docx

• Название темы.docx

• Направление подготовки специальность 42.doc

• Тесты по дисциплине Планирование и бюджетирование в государственном и муниципальном управлении.doc