Файл: Контрольная работа по дисциплине Телетрафик сетей последующего поколения.docx

Министерство образования и науки Нижегородской областиГосударственное бюджетное образовательное учреждение высшего образования«Нижегородский государственный инженерно-экономический университет»(ГБОУ ВО НГИЭУ)Институт: «Информационные технологии и системы связи»Кафедра: «Инфокоммуникационные технологии и системы связи»КОНТРОЛЬНАЯ РАБОТАпо дисциплине: «Телетрафик сетей последующего поколения»вариант 4 Выполнил студентИнститута ИТиССзаочной формы обучения1 курса группы 22 МгИФЗ_______ Синяев Р.К.Проверил: к.т.н., доцент _______ Сорокин И.А.г. Княгинино2023

Оглавление

Введение

Основная цель теории телетрафика заключается в разработке методов оценки качества функционирования систем распределения информации. В соответствии с этим на первом месте в теории телетрафика стоят задачи анализа, т.е. отыскание зависимостей и значений величин, характеризующих качество обслуживания, от характеристик и параметров входящего потока вызовов, схемы и дисциплины обслуживания. Эти задачи в начальный период развития телефонной техники были более актуальными, чем задачи синтеза, и решались, как правило, с помощью теории вероятностей.Поэтому наиболее значительные результаты на сегодняшний день получены при решении задач анализа.Развитие координатной и особенно квазиэлектронной и электронной коммутационной техники поставило перед теорией телетрафика сложные вероятностно-комбинаторные задачи синтеза, в которых требуется определить структурные параметры коммутационных систем при заданных потоках, дисциплине и качестве обслуживания.Близкими к задачам анализа и синтеза являются задачи оптимизации. Эти задачи при проектировании систем распределения информации формулируются следующим образом: определить такие значения структурных параметров коммутационной системы (алгоритмы функционирования), для которых:

---

при заданных потоках, качестве и дисциплине обслуживания стоимость или объем оборудования системы распределения информации минимальны ипри заданных потоках, дисциплине обслуживания и стоимости качественные показатели функционирования системы распределения информации оптимальны.При эксплуатации систем распределения информации задача оптимизации формулируется как задача управления потоками вызовов или структурой системы для достижения наилучших показателей качества функционирования. Из-за больших вычислительных трудностей задачи оптимизации систем распределения информации начали ставиться и решаться в последние два десятилетия после появления быстродействующих ЭВМ.

1. Представьте входящие потоки заявок. Повторные вызовы

Потоком вызовов (в общем случае – событий) называется последовательность вызовов, поступающих через какие-либо интервалы или в какие-либо моменты времени. В теории массового обслуживания под потоком вызовов принято понимать не только последовательность вызовов, поступающих от группы абонентов или группы устройств телефонной сети, но и другие последовательности событий, например поток телеграмм, поток писем, поток неисправностей отдельных коммутационных устройств или телефонных сооружений в целом, поток информации, поступающей на ЭВМ, поток неисправностей в станках и т.п. Рассматриваемые в настоящей главе свойства, характеристики, закономерности потоков вызовов не ограничиваются узкими рамками изучения потоков телефонных вызовов, а имеют более широкую область применения.Следует различать детерминированный и случайный потоки вызовов. Детерминированный поток вызовов с последовательность вызовов, в которой вызовы поступают в определенные, строго фиксированные неслучайные моменты или через определенные, строго фиксированные, неслучайные промежутки времени. Случайный поток вызовов отличается от детерминированного тем и только тем, что моменты поступления вызовов и промежутки времени между вызовами являются не строго фиксированными, а случайными величинами.Детерминированные потоки являются частным случаем случайных потоков и на практике встречаются редко. Примерами их могут служить: поток сеансов связи с искусственными спутниками Земли, поток поступления деталей и выхода изделий ритмично работающего завода и т.п. Строго говоря, даже в таких потоках часто имеют место случайности. В связи с этим в теории телетрафика основное внимание уделяется рассмотрению случайных потоков вызовов.

---

Условимся в дальнейшем случайные величины обозначать прописными (большими) буквами, а их возможные значения с соответствующими строчными (малыми) буквами.Поток вызовов может быть определен тремя эквивалентными способами: последовательностью вызывающих моментов t₁, t₂, …, t_n, последовательностью промежутков времени между вызывающими моментами z₁, z₂, …, z_n и последовательностью чисел k₁, k₂,…, k_n, определяющих количество вызовов, поступающих в течение заданных отрезков времени (t₀, t₁), (t₀, t₂),…, (t₀, t_n). При этом под вызывающим моментом понимается момент одновременного поступления одного, двух и более вызовов; для вызывающих моментов всегда, если t_i>t_i-1, то z_i>0, в то время как для момента поступления вызова t_i≥t_i-1 и z_i ≥0.Определение случайного потока вызовов связано с определением в вероятностном смысле либо последовательности вызывающих моментов, либо последовательности промежутков между вызывающими моментами, либо последовательности чисел вызовов, поступающих в течение отрезков времени (t₀, t₁), (t₀, t₂), …, (t₀, t_n).Для задания случайных потоков вызовов, как и любых других случайных величин и процессов, используются функции распределения. Функцией распределения вероятностей некоторой случайной величины X называется функция 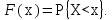(1)определяющая вероятность того, что Х<х, где х - определенная, заданная величина. С учетом изложенного, для задания случайного потока вызовов могут быть использованы следующие эквивалентные способы:

• 
  совместный закон распределения п случайных вызывающих моментов
  

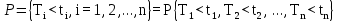. (2)где T_i – i-й вызывающий момент; n может принимать любое значение;

• 
  совместный закон распределения n случайных промежутков времени между вызывающими моментами
  

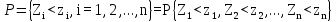. (3)где Z_i – промежуток времени между (i - 1) - и i-м вызывающими моментами

---

; n может принимать любое значение;

• 
  совместный закон распределения числа вызовов К на n отрезках времени (t₀, t₁), (t₀, t₂),…, (t₀, t_n):
  

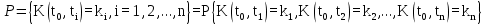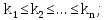
, (4)где n может принимать любое значение; 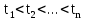.Введем некоторые ограничения на рассматриваемые случайные потоки вызовов.Потоки вызовов подразделяются на неоднородные и однородные. В неоднородном потоке вызовов каждый вызов имеет две и более характеристики. Например, вызовы, поступающие от абонентов телефонной сети, определяются моментами их поступления, направлениями установления соединений, длительностью их обслуживания и другими характеристиками.Аналогично телеграммы, поступающие на телеграф, характеризуются моментами их поступления, направлениями их передачи, количеством слов в телеграмме и т.д.Однородный поток вызовов характеризуется последовательностью, определяющей только закономерность поступления вызовов, т.е. последовательностью моментов поступления вызовов или промежутков времени между вызовами, либо иным способом задания потока вызовов.На практике потоки вызовов, как правило, являются неоднородными. Несмотря на это, целесообразно отдельно от других характеристик потоков вызовов изучить последовательности моментов поступления вызовов. Поэтому в дальнейшем под потоком вызовов будем понимать однородный поток вызовов.Ограничимся рассмотрением потоков, в которых на любом конечном отрезке времени поступает конечное число вызовов и математическое ожидание числа поступающих вызовов также является конечной величиной. Такие потоки называются финитными.Математическое ожидание числа вызовов, поступающих в интервале времени (0, t), называется ведущей функцией потока. Обозначим эту функцию ∆(0, t). Функция ∆(0, t) - неотрицательная, неубывающая и в практических задачах принимает конечное значение.Потоки с непрерывной ведущей функцией называются регулярными, а со ступенчатой - сингулярными. Вероятность поступления хотя бы одного вызова в определенный момент времени для регулярного потока равна нулю, а для сингулярного потока в моменты разрыва ведущей функции отлична от нуля. Нас интересуют только потоки вызовов с непрерывной ведущей функцией, т.е. регулярные потоки.

---

Таким образом, в дальнейшем рассматриваются случайные однородные финитные регулярные потоки.Система, на которую поступает поток вызовов, обслуживает не все поступающие вызовы. Часть из них не обслуживается (теряется) по ряду причин. Так, например, на телефонных сетях часть вызовов не обслуживается по причине занятости или неответа вызываемого абонента, ошибок вызывающего абонента в процессе набора номера, занятости всех соединительных устройств, способных обслужить поступивший вызов, не установление соединения коммутационной системой по техническим причинам. Все или часть источников необслуженных вызовов осуществляют повторные вызовы.Поток с повторными вызовами состоит из первичных и повторных вызовов. Поскольку параметр потока повторных вызовов зависит от состояния коммутационной системы, то и поток с повторными вызовами относится к классу потоков с простым последействием.Параметр потока повторных вызовов можно определить как произведение числа источников повторных вызовов j на параметр одного источника β. В качестве модели потока первичных вызовов принимается простейший с параметром λ или примитивный с параметром λi поток. Параметр суммарного потока равен сумме параметров потоков первичных и повторных вызовов. Для простейшего и примитивного потоков он соответственно составляет 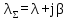; . (5)

2. Разъясните потоки с простым последействием. Симметричный и примитивный потоки

Основной характеристикой потока с простым последействием является зависимость параметра потока от состояния коммутационной системы в любой момент времени t.Коммутационная система имеет множество состояний s, которые различаются числом занятых входов, выходов и соединительных путей между входами и выходами коммутационной системы, номерами занятых входов и выходов, номерами соединительных путей между входом и выходом, числом занятых или свободных источников вызовов и т.д.Так как коммутационная система всегда имеет конечное число входов, выходов, соединительных путей, то конечным является и число возможных состояний системы обслуживания (хотя оно может быть и очень велико). Такие состояния коммутационной системы будем называть микросостояниями. Состояния коммутационной системы, различающиеся только числом занятых входов (или выходов), называются макросостояниями.

---