Файл: Контрольная работа по дисциплине Телетрафик сетей последующего поколения.docx

Исследования процесса обслуживания коммутационной системой поступающего потока вызовов следует производить с учетом микросостояний системы в тех случаях, когда структура рассматриваемой коммутационной системы такова, что вероятность ее состояния в любой произвольный момент времени t зависит как от числа занятых входов (или выходов), так и от того, какие именно входы (или выходы) заняты и по каким соединительным путям осуществляются соединения между каждым входом и выходом. Если же структура рассматриваемой коммутационной системы такова, что вероятности ее состояний в любой произвольный момент t зависят только от числа занятых входов (или выходов), то исследования процесса обслуживания коммутационной системой поступающих вызовов можно производить только с учетом макросостояний системы.

Под параметром потока в состоянии s(t) будем понимать предел

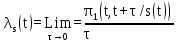, (6)

где π₁(t, t+τ/s(t)) – вероятность поступления за промежуток (t, t+τ) одного и более вызовов, если в момент t коммутационная система находится в состоянии s(t). Это определение позволяет сформулировать понятие потока с простым последействием. Под потоком с простым последействием понимается ординарный поток, для которого в любой момент времени t существует конечный параметр потока в состоянии s(t) (6), зависящий только от состояния s(t) коммутационной системы в момент t и не зависящий от процесса обслуживания вызовов до момента t.

(Параметр потока с простым последействием в любой момент времени t зависит от состояния системы в этот момент времени, а состояние системы s(t), в свою очередь, зависит от процесса, поступления и обслуживания вызовов до момента t. Такое последействие принято называть простым, поскольку для определения; параметра потока в момент t достаточно ограничиться знанием; состояния системы s(t) в этот момент. Поток с простым последействием является нестационарным, так как его параметр зависит от момента t. Заметим, что эта зависимость проявляется через состояние s(t). Для каждого конкретного состояния параметр; потока с простым последействием является постоянной величиной.

Понятие потока с простым последействием является одним из самых общих в теории потоков. Практически любой поток вызовов можно считать потоком с простым последействием, поскольку коммутационная система всегда влияет на процесс поступления вызовов. К частным случаям потока с простым последействием относятся симметричный поток, примитивный поток и поток с повторными вызовами.

---

Симметричным потоком называется поток с простым последействием, параметр которого λs(t) в любой момент времени t зависит только от числа i обслуживаемых в этот момент вызовов и не зависит от других характеристик, определяющих состояние s(t) коммутационной системы. При этом зависимость параметра от числа обслуживаемых вызовов может быть подчинена любому закону. Поэтому в любом состоянии s(t) с i обслуживаемыми вызовами параметр симметричного потока один и тот же, он зависит только от i, т.е. λs(t)=λi.

Примитивным называется такой симметричный поток, параметр которого λi прямо пропорционален числу свободных в данный момент источников:

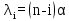, (7)

где n - общее число источников вызовов; i - число занятых источников; α - параметр потока источника в свободном состоянии (при этом имеет место естественное предположение - занятый источник не может производить вызовы). В модели примитивного потока параметр α источника в свободном состоянии является постоянной величиной, а параметр примитивного потока λi убывает с увеличением числа занятых источников i. Математическое ожидание параметра примитивного потока λ определяется по формуле

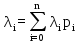, (8)

где p_i - вероятность того, что в системе занято i источников. Заметим, что в обслуживающей примитивный поток коммутационной системе не требуется соединительных устройств более n, так как занятый источник не может производить вызовы.

Можно показать, что функция распределения вероятностей длительности свободного состояния источника (промежутка времени между моментом окончания одного занятия и моментом поступления от источника нового вызова)

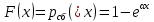, (9)

Таким образом, промежуток времени между моментами окончания одного занятия и поступления от источника нового вызова распределен по показательному закону. Следовательно, поток вызовов от свободного источника является простейшим.

Поток с простым последействием является более общим по сравнению с простейшим потоком вызовов. Простейший поток можно представить частным случаем потока с простым последействием, в том числе симметричного и примитивного потоков. С увеличением числа источников п и уменьшением параметра α последействие потока уменьшается. В предельном случае при

---

n→∞ и α→0 так, что nα есть конечная величина и iпринимает ограниченные значения, параметр потока λ=nα не зависит от состояния системы, т.е. модель примитивного потока переходит в модель простейшего потока вызовов.

3. Представьте поток с ограниченным последействием. Поток Пальма

Под потоком с ограниченным последействием понимается поток вызовов, у которого последовательность промежутков времени между вызовами z₁, z₂, … представляет последовательность взаимно независимых случайных величин, имеющих любые функции распределения. Такой поток вызовов описывается последовательностью функций распределения промежутков между вызовами:

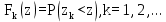(10)

Как следует из приведенного определения потока с ограниченным последействием, свойство ограниченности последействия заключается в независимости промежутков между вызовами. Введенное ранее понятие «отсутствие последействия» потока заключается в независимости количества вызовов, поступающих в непересекающиеся отрезки времени. Таким образом, свойства «ограниченность последействия» и «отсутствие последействия» являются различными характеристиками потока.

Частным случаем потока с ограниченным последействием является рекуррентный поток, который характеризуется одинаково распределенными промежутками времени между вызовами:

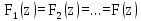. (11)

Некоторым обобщением рекуррентного потока является рекуррентный поток с запаздыванием с поток с ограниченным последействием, для которого

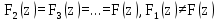. (12)

Стационарный ординарный рекуррентный поток с запаздыванием называется потоком Пальма. Для потока Пальма, как и для любого другого стационарного ординарного потока, µ=λ=1/M(Z). Распределение промежутков времени между вызовами для потока Пальма задается следующими соотношениями:

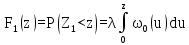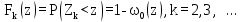; (13)

где ω₀(z) - вероятность отсутствия вызовов на промежутке времени длиной z. Весьма важной является следующая теорема Пальма (доказательство этой теоремы не приводится): если на коммутационную систему с потерями и с показательным распределением длительности обслуживания поступают вызовы, образующие поток Пальма, то поток необслуженных вызовов является также потоком Пальма. В частности, если поток поступающих вызовов будет простейшим, то поток потерянных вызовов будет потоком Пальма.

---

Это справедливо и для потоков, теряемых каждой линией полнодоступного пучка, работающего в режиме упорядоченного искания: если на первую линию пучка поступает поток Пальма или простейший поток вызовов, то поток потерянных вызовов любым количеством первых линий пучка будет потоком Пальма.

Простейший поток является частным случаем потока Пальма, у которого все промежутки времени между вызовами, включая первый, распределены по показательному закону. При вероятности ω соотношения (13) преобразуются к соотношению

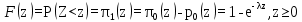(14)

Рекуррентный поток без запаздывания является ординарным потоком. Рекуррентные потоки с запаздыванием могут быть и неординарными. Доказано, что стационарный рекуррентный поток, является простейшим.

Список использованной литературы

1. 
   Наумов В.А., Самуйлов К.Е., Яркина Н.А. Теория телетрафика мультисервисных сетей. - М.: РУДН, 2008. - 191 с.
   
2. 
   Деарт В.Ю. Мультисервисные сети связи. 4.2: Протоколы и системы управления сеансами (Softswitch/IMS). - М.: Брис-М, 2011. – 198 с.
   
3. 
   Лагутин, Владимир Сергеевич Защита абонентского телетрафика. Учебное пособие. Гриф УМО МО РФ / Лагутин Владимир Сергеевич. – М.: Машиностроение, 2012. – 411 c.
   
4. 
   Летников А.И., Пшеничников А.П., Гайдамака Ю.В., Чукарин А.В. Системы сигнализации сетей коммутации каналов и коммутации пакетов: Уч. Пособие. - М.: МТУСИ, 2008. – 195 с.
   
5. 
   Наумов В.А., Самуйлов К.Е., Яркина Н.А. Теория телетрафика мультисервисных сетей. - М.: РУДН, 2008. - 191 с.
   
6. 
   Степанов, С.Н. Основы телетрафика мультисервисных сетей / С.Н. Степанов. – М.: Эко-Трендз, 2010. – 750 c.
   

---