Добавлен: 06.11.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
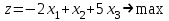
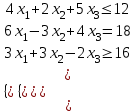
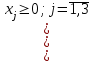
Графический метод
Для графического решения преобразуем систему уравнений:
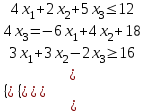
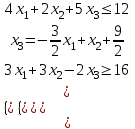
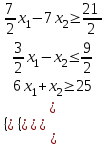
Целевая функция будет выглядеть следующим образом:
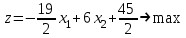
Ограничения задачи ЛП заданы неравенствами, значит это стандартная задача её можно решить графическим методом.
-
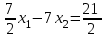, точки для построения (3;0) и (1;-1); решение – полуплоскость выше прямой; -
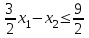
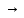
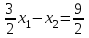, точки для построения (3;0) и (1;-3); решение – полуплоскость ниже прямой; -
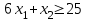
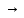
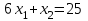, точки для построения (4;1) и (3;7); решение – полуплоскость выше прямой;
Строим нулевой уровень ЦФ
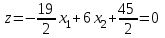,прямая проходит через начало координат (0;0), вектор градиент функции 
.
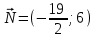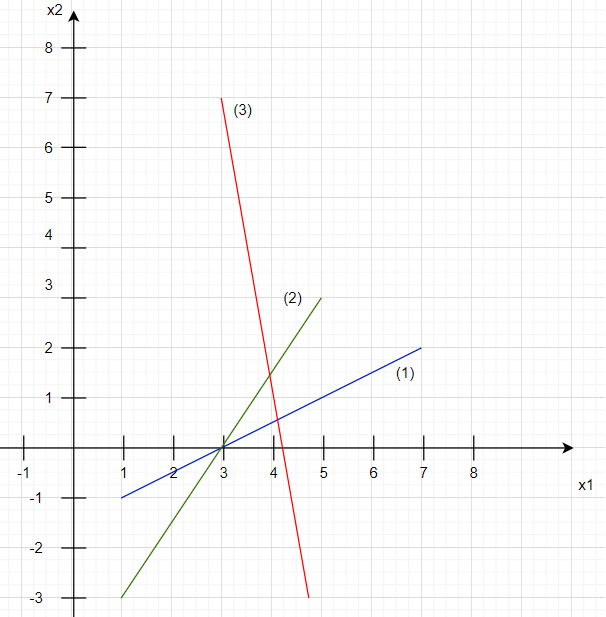
Данная задача не имеет решений, так как ОДР – пустое множество.
Ответ: Решений нет.
-
Симплекс метод.
Необходимо привести исходные уравнения к канонической форме:
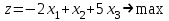
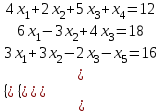
Запишем расширенную матрицу для данной системы:
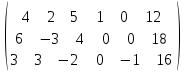
Ранг матрицы равен 3.
Базисные переменные -
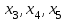.I базисное решение – (0;0;
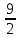;12;-16) – не является допустимым.Переходим к методу искусственных переменных для поиска ДБР.
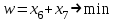
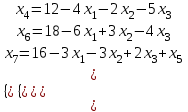
Базисные переменные -
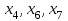.БР: (0;0;0;12;0;18;16)
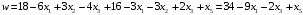–ДБР, т.к. параметры БР не отрицательные, т.е. новая оптимизационная задача сформирована и имеет ДБР, поэтому мы можем запустить симплекс-алгоритм для поиска оптимального решения.-
Симплекс-алгоритм.
Полученное ДБР не является оптимальным решением, так как есть отрицательные коэффициенты.
При увеличении x1 функция убывает быстрее, поэтому:
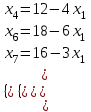
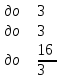
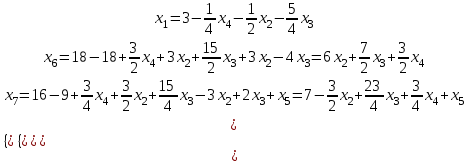
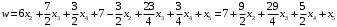
Оптимальное решение, так как все коэффициенты положительные.
Отсюда следует, что решений с w=0 не существует, т.е. исходная задача оптимального решения не имеет.
Ответ: нет решений.