ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 83
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
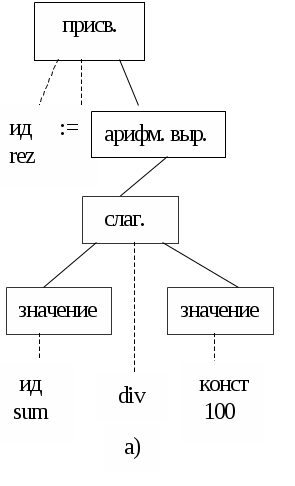
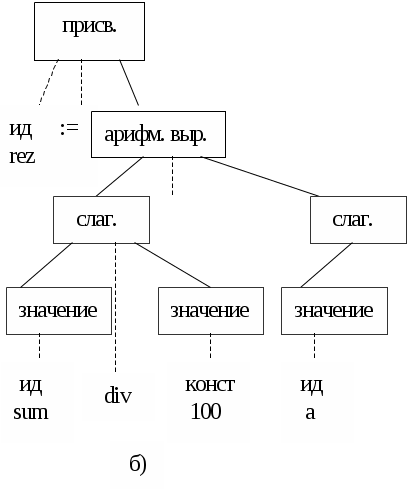
Рис. 10
Мы привели примеры грамматического разбора отдельных предложений методом рекурсивного спуска. Однако, этот метод применим и ко всей программе в целом. В этом случае для осуществления синтаксического анализа следует просто обратиться к процедуре, соответствующей нетерминальному символу программа.
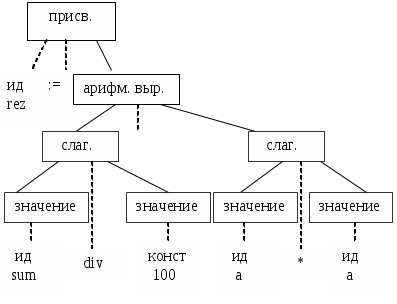
Рис. 11
В результате работы этой процедуры будет построено дерево грамматического разбора для всей программы.
4. Метод операторного предшествования
Этот метод относится к восходящим (метод снизу вверх), которые начинают разбор с конечных узлов грамматического дерева и пытаются объединить их построением узлов все более и более высокого уровня до тех пор, пока не будет достигнут ,корень дерева. Метод операторного предшествования основан на анализе пар последовательно расположенных операторов исходной программы и решением вопроса о том, какой из них должен выполняться первым. Рассмотрим, например, арифметическое выражение
А + В*С-В.
В соответствии с обычными правилами арифметики умножение и деление осуществляются до сложения и вычитания. Можно сказать, что умножение и деление имеют более высокий уровень предшествования, чем сложение и вычитание. При анализе первых двух операторов (+,*), выяснится, что оператор + имеет более низкий уровень предшествования, чем оператор *. Часто это записывают следующим образом:
+ <•*
Аналогично для следующей пары операторов (* и -) оператор * имеет более высокий уровень предшествования, чем оператор -. Мы можем записать это в виде
*•>-
Метод операторного предшествования использует подобные отношения между операторами для управления процесса грамматического разбора. В частности, для рассмотренного арифметического выражения мы получили следующие отношения предшествования:
А+ В*С –В
Отсюда следует, что подвыражение В*С должно быть вычислено до обработки любых других операторов рассматриваемого выражения. В терминах дерева грамматического разбора это означает, что операция * расположена на более низком уровне узлов дерева, чем операция + или -. Таким образом, рассматриваемый метод грамматического разбора должен распознать конструкцию В*С, интерпретируя ее в терминах заданной грамматики, до анализа соседних термов предложения.
Предшествующее изложение иллюстрирует основную идею, на которой основан метод грамматического разбора, построенный на отношения операторного предшествования. В рамках этого метода предложение сканируется слева направо до тех пор, пока не будет найдено подвыражение, операторы которого имеют более высокий уровень предшествования, чем соседние операторы. Далее это подвыражение распознается в терминах правил вывода используемой грамматики. Этот процесс, продолжается до тех пор, пока не будет достигнут корень дерева, что и будет означать окончание процесса грамматического разбора. Далее мы рассмотрим приложение описанного подхода к нашему примеру программы (рис. 1). Грамматика этого предложения имеет вид, представленный на рис. 2.
Первым шагом при разработке процессора грамматического разбора, основанного на методе операторного предшествования, должно быть установление отношений предшествования между операторами грамматиками. При этом под оператором понимается любой терминальный символ (т.е. любая лексема). Таким образом, мы должны, в частности, установить отношения предшествования между лексемами begin, read, (. Приведем матрицу, которая задает отношения предшествования для нашей грамматики (табл. 4)).
Каждая клетка этой матрицы определяет отношение предшествования (если оно существует) между лексемами, соответствующими строке и столбцу, на пересечении которых находится эта клетка. Например, мы видим, что
program = var и
begin <• read
Отношение = означает, что обе лексемы имеют одинаковый уровень предшествования и должны рассматриваться грамматическим процессором в качестве составляющих одной конструкции языка. Обратите внимание, что для отношения предшествования не выполняются некоторые правила, привычные для отношения арифметического порядка. Например,
; •> end, . но end •> ;
Обратите внимание также на то, что для многих пар лексем отношения предшествования не существует. Это означает, что соответствующие пары лексем не могут находиться рядом ни в каком грамматически правильном предложении. Если подобная комбинация лексем все же встретится в процессе грамматического разбора, то она должна рассматриваться как синтаксическая ошибка.
Для применимости метода операторного предшествования необходимо, чтобы отношения предшествования были заданы одиозначно, например, не должно быть одновременно отношений ; <• begin и ; >• begin. Это требование выполняется для нашей грамматики, однако, ввиду, что несущественные ее изменения могут привести к тому, что некоторые из отношений перестанут быть однозначными и метод операторного предшествования станет не применимым.
Приведем пример разбора с помощью операторного предшествования. Пусть анализируется предложение read из нашей программы. Это предложение анализируется по лексемам слева направо. Для каждой пары соседних операторов определено отношение предшествования
begin read ( ид. ) ;
<• = <•. •> •>
begin read (
<• = = •>
begin
<•
На первом шаге процессор грамматического разбора выделим фрагмент ограниченный отношениями <• и •> для распознавания в терминах грамматики. В данном случае этот фрагмент содержит единственную лексему ид.. Эта лексема может быть распознана как нетерминал <значение> в соответствии с правилом из грамматики. Однако, эта лексема может быть также распознана как нетерминальный символ <список переменных>. Для рассматриваемого метода не важно, какой конкретно нетерминальный символ распознан. Лексема ид интерпретируется просто как некий нетерминальный символ <N1>. Конструкция read(<N1>) интерпретируется как один нетерминальный символ <N2>.
На этом разбор предложения READ закончено. Если мы сравним деревья грамматического разбора для этого предложения, то увидим, что они полностью совпадают, за исключением имён нетерминальных символов.
Рассмотрим грамматический разбор для оператора
; rez: = sum DIV 100 - А * А ;
< = < > < > < > < >
; rez :=
< = < > < >
; rez :=
< = < >
; rez :=
< = >
При этом дерево грамматического разбора имеет вид, представленный на рис. 12.
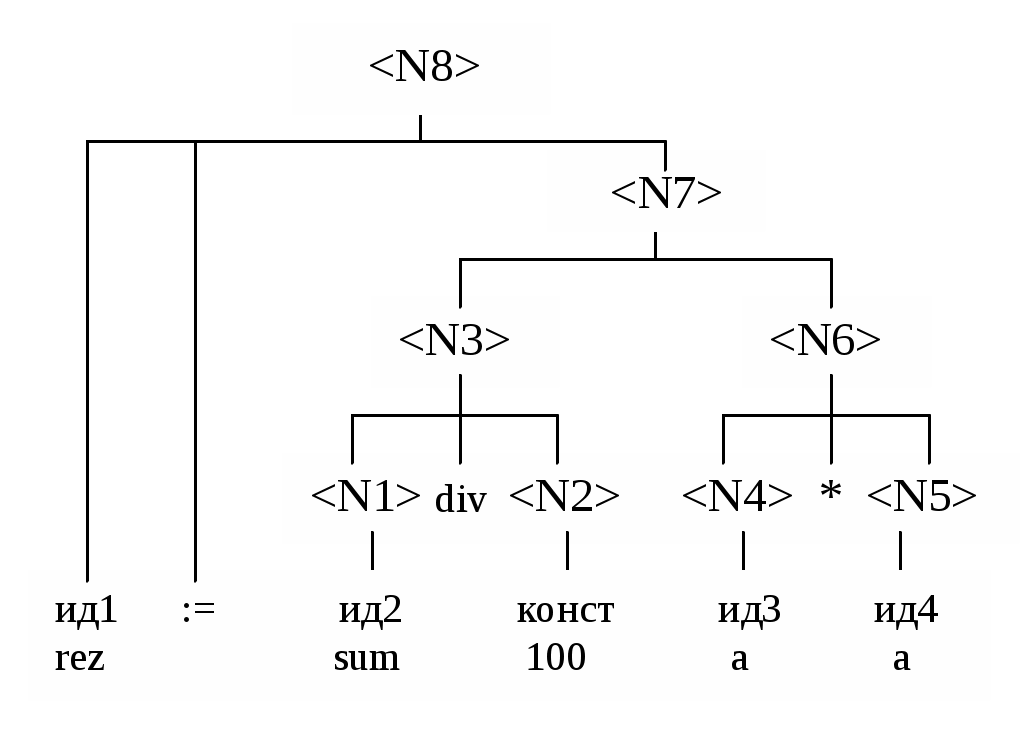
Рис. 12
Заметим еще раз, что процесс грамматического разбора начинается слева направо и продолжается на каждом шаге до тех пор, пока не определится очередной фрагмент предложения для грамматического распознавания, т.е. первый фрагмент, ограниченный отношениями <• и •>. Как только подобный фрагмент выделен, он интерпретируется как некоторый очередной нетерминальный символ в соответствии с каким-нибудь правилом грамматики. Этот процесс продолжается до тех пор, пока предложение не будет распознано целиком.
Обратите внимание, что каждый фрагмент дерева грамматического разбора строится, начиная с конечных узлов вверх, в сторону корня дерева. Отсюда и возник термин восходящий разбор. Если мы рассмотрим дерево грамматического разбора, исходя из грамматики языка (рис. 2), то увидим, что оно несколько отличается от полученного методом операторного предшествования дерева (рис. 12).
Например, идентификатор sum был сначала интерпретирован как <значение>, а потом как <слагаемое>, являющийся одним из операндов операции DIV. При разборе методом операторного предшествования идентификатор sum был интерпретирован как единственный нетерминал
Они вытекают из свободы образования имен нетерминальных символов, распознаваемых в рамках метода операторного предшествования. Интерпретация sum сначала как <значение>, а потом как <слагаемое> является просто переименованием нетерминальных символов. Такое переименование необходимо, поскольку в соответствии с грамматикой (правило 8) первым операндом операции умножения должен быть <слагаемое>, а не <значение>. так как для нашего метода имена нетерминальных символов несущественны, то подобные переименования становятся ненужным. Собственно говоря, три различных имени: <арифметическое выражение>, <слагаемое>, <значение> - были включены в грамматику только как средства описания отношения предшествования между операторами (например, для указания того, что умножение следует выполнять после сложения). Поскольку эта информация содержится в нашей матрице предшествования, то становится ненужным различать эти три имени в процессе грамматического разбора.
Возможный алгоритм метода операторного предшествования приведен на рис. 13.
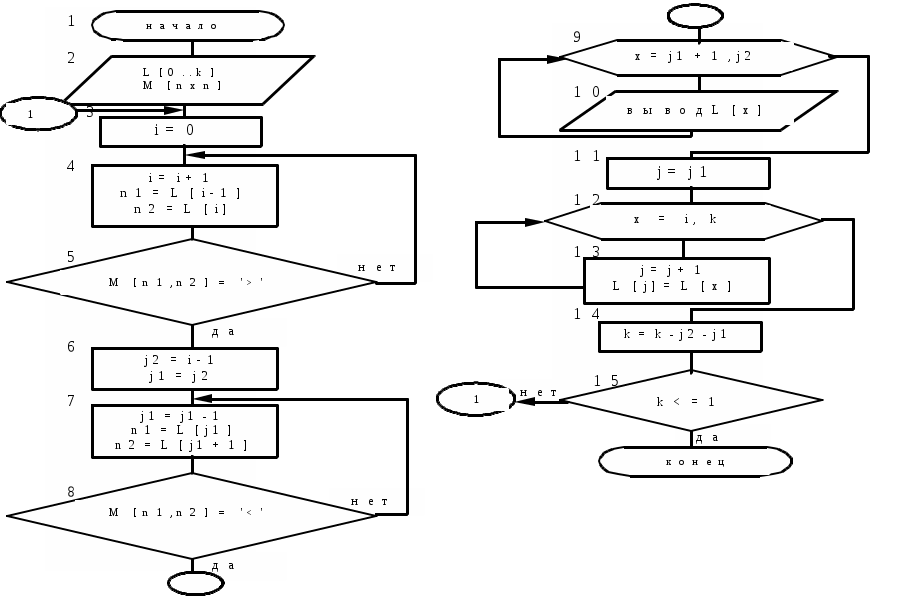
Рис. 13
В данном алгоритме первоначально просматривается цепочка лексем (массив L), устанавливается отношение предшествования между соседними лексемами по таблице отношений предшествования (матрица M[nxn]) до тех пор , пока не встретится отношение '>' (блоки 4 – 5). После этого возвращаемся по массиву лексем назад, пока между лексемами не встретится отношение '<' (блоки 7 – 8). Затем лексемы, ограниченные отношениями '< >', записываются во внутреннее представление (блоки 9 – 10) . В блоках 12 – 14 элементы массива лексем сдвигаются на длину выведенной цепочки. Так продолжается, пока не распознана вся последовательность лексем.
5. Внутреннее представление программы
На выходе синтаксического анализатора формируется программа во внутреннем представлении. Существует несколько различных способов представления программы в некоторой промежуточной форме для анализа и оптимизации кода: последовательность четверок, последовательность троек, постфиксная запись, префиксная запись, синтаксическое дерево.
1. Последовательность четвёрок
Каждая четвёрка записывается в виде:
операция ор1, ор2, результат
где операция – выполняемая объектным кодом функция; ор1, ор2 – операнды этой операции; результат определяет, куда должно быть помещено результирующее значение.
Например, предложение исходной программы (рис. 1): sum:=sum+а может быть представлено четвёрками следующим
образом:
+ sum , а , I1
:= I1 , , sum
Здесь I1 обозначает промежуточный результат (sum+а), вторая четвёрка присваивает это значение переменной sum.
Все четвёрки расположены в том порядке, в котором должны выполняться соответствующие инструкции объектного кода, что существенно облегчает анализ для оптимизации кода. Это означает также, что трансляция в машинные коды будет относительно простой. В таблице 3 представлена последовательность четвёрок, соответствующая исходной программе.
За операциями геаd и write следует четвёрка Param, определяющая параметры операций read и write. Четвёрка Param будет, разумеется, при окончательной генерации машинного кода оттранслирована в список параметров. Операция > в четвёрке 3 сравнивает значение двух своих операндов и осуществляет переход к четвёрке 9, если первый
Таблица 5
| | Операция | Операнд 1 | Операнд 2 | Результат |
| № | 1 | 2 | 3 | 4 |
| 1 | : = | #0 | | Sum |
| 2 | := | #1 | | I |
| 3 | > | I | #100 | 9) |
| 4 | read | | | |
| 5 | param | а | | |
| 6 | + | sum | а | I1 |
| 7 | : = | I1 | | sum |
| 8 | goto | | | 3) |
| 9 | div | sum | #100 | I1 |
| 10 | * | а | а | I3 |
| 11 | - | I2 | I3 | I4 |
| 12 | := | I4 | | геz |
| 13 | write | | | |
| 14 | Param | rez | | |
| 15 | Рагаm | sum | | |
операнд больше второго. Операция goto в четвёрке 8 осуществляет безусловный переход к четвёрке 3.
Таким образом, последовательность четвёрок и является результатом работы синтаксического анализатора.
2. Постфиксная запись
Обычно программа осуществляет те или иные действия над данными. Соответствующие операции программист записывает, используя инфиксную форму записи, в которой знак операции ставится между операндами. Например: ( А + В ) * С.
Вычисление такого выражения является непростой задачей. Операцию умножения нельзя выполнить до тех пор, пока не будет прочитан второй операнд С. Если этот операнд сам является сложным выражением, то прежде, чем выполнить умножение, необходимо считать много данных из текста программы.
Отмеченные трудности можно легко обойти, если использовать другую форму записи операций. Она называется постфиксной и отличается тем, что знак операции ставится непосредственно за операндами. Такая запись обладает двумя ценными свойствами, благодаря которым ее используют как промежуточную форму представления исходной программы при трансляции:
1) Для записи любого выражения не нужны скобки. Так как оператор непосредственно следует за операндами, участвующими в операции, неопределенность в указании операндов отсутствует. Например, выражение ( А + В ) * С в постфиксной записи имеет вид:
А В + С *.
2) К моменту считывания очередного оператора соответствующие операнды уже прочитаны. Поэтому оператор может быть выполнен без чтения каких либо дополнительны данных.
Сказанное выше относится к бинарным операциям, однако не трудно распространить результаты рассуждений и на унарные операции. Однако при этом могут возникнуть сложности. Например, знак " - " может стоять в инфиксной записи, указывая как бинарную, так и унарную операцию, и его правильный смысл становится очевидным из контекста. В постфиксной записи сделать это труднее. Унарный минус и другие унарные операции можно представлять двумя способами: либо записывать их как бинарные операции, например вместо " - В " писать " 0 - В "; либо для обозначения унарных операций вводить новый символ, например, выражение А + ( - В + С * Е ) в постфиксной форме примет вид: А В @ С Е * + + .
6. Генерация кода
Возможны три формы объектного кода: абсолютные команды, помещенные в фиксированные ячейки (после окончания компиляции такая программа немедленно выполняется); программа на автокоде (ее потом придется транслировать);