МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ОБРАЗОВАНИЯ

«НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

ФАКУЛЬТЕТ БИЗНЕСА

Кафедра Экономической информатики

РЕФЕРАТ «Неравенство Рао-Крамера»

по дисциплине

«Теория вероятностей и математическая статистика»

Выполнил:		Проверил:
Студент	Ершова Клара	Преподаватель	Джафаров К. А.
Факультет	Факультет бизнеса
Направление (специальность) подготовки	38.03.05 Бизнес-информатика	Балл: _________
Группа	ФБИ–12	Оценка _________________
Шифр	090542249
____________________________		____________________________
Подпись студента		Подпись преподавателя
Дата сдачи:	«__» _мая_2023г.	Дата защиты:	«__» _мая_2023г.

Новосибирск 2023

Неравенство Рао-Крамера

Неравенство Рао-Крамера является одним из основных инструментов теории оценивания параметров статистических моделей. Оно устанавливает нижнюю границу для дисперсии несмещенных оценок параметров. Таким образом, неравенство определяет, насколько точно можно оценить параметры статистической модели.

Неравенство Рао-Крамера 

---

— это математическое неравенство, которое связывает дисперсию несмещённой оценки * неизвестного параметра  оценки и информацию Фишера, полученную из выборки. Данная теорема используется для получения нижней границы дисперсии D_* оценки *.

Формулировка неравенства Рао-Крамера связывает дисперсию несмещенной оценки с информацией Фишера, которая является мерой информативности выборки относительно параметра. Если информация Фишера высока, то выборка содержит много информации о параметре, и дисперсия оценки будет низкой. Если же информация Фишера низкая, то выборка содержит мало информации о параметре, и дисперсия оценки будет высокой.

Оценки, для которых будет достигаться нижняя грань для дисперсии будут называться эффективными оценками.

Неравенство Рао-Крамера также связано с понятием асимптотической эффективности. Если метод оценивания параметров удовлетворяет условиям неравенства Рао-Крамера, то он является асимптотически эффективным. Это значит, что при увеличении объёма выборки оценки параметров будут стремиться к истинным значениям со скоростью, которая является наилучшей из всех возможных методов оценивания.

К распределению предъявляются некоторые условия, а именно условия регулярности:

1. 
   Параметрическое множество – интервал (лежит в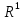 ) и для каждого возможного значения параметра 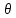из этого интервала и для каждого X существует производная по 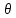. То есть, в случае распределения непрерывного типа функции 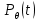непрерывно дифференцируемы по 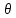для почти всех t, а интегралы
   

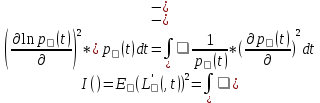
существуют и непрерывны .

---

2. 
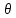   В случае распределения дискретного типа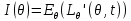 ² существует, положительна и непрерывна во всех точках . Ряды сходятся абсолютно и равномерно в ¹.
   

Пусть существует выборка X₁, …, X_n – независимые одинаково распределенные случайные величины, у которых есть неизвестное распределение, которое принадлежит некоторому классу распределений

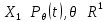
Рассмотрим функцию плотности из распределения L(t, ) = ln p_ (t) – необходимо найти ее производную по :



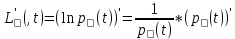
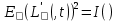- информативное количество Фишера

Информационное число Фишера можно интерпретировать как количество информации, содержащейся в выборке относительно параметра . Чем больше это число, тем точнее можно оценить .

Предполагается, что выполняются условия регулярности и тогда имеет место теорема неравенства.

Теорема (Неравенство Рао-Крамера): пусть выполнены условия регулярности (R). Тогда для оценки 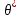неизвестного параметра справедливо следующее неравенство: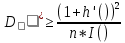



Из теоремы следует, что

1. 
   При выполнении условий теоремы справедливо неравенство
   

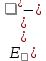
если же * — несмещенная оценка, то справедливо неравенство

2. 
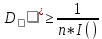
   Если выполнено условие (R) и в неравенстве Рао-Крамера достигается равенство, то * — эффективная оценка в классе оценок со смещением h (), т.е.
   

---

Таким образом, неравенство Рао-Крамера является одним из ключевых инструментов теории оценивания параметров статистических моделей. Его применение позволяет определить, насколько точно можно оценить параметры модели, сравнить различные методы оценивания параметров и выбрать наиболее эффективный метод для конкретной задачи.

---

Смотрите также файлы

• Анализ рисков. Изменение погод.docx

• Немецкий и английский язык и литература.docx

• Отчет по лабораторной работе 5 Изучение основного закона динамики вращательного движения.docx

• Задание Какие изменения в личностной сфере ребёнка происходят в связи с поступлением в школу.docx

• Лабораторная работа 8 по дисциплине Организация систем управления и диагностики.docx