Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Магнитогорский государственный технический университет им. Г.И. Носова»

(ФГБОУ ВО «МГТУ им. Г.И. Носова»)


Кафедра Физики

ЛАБОРАТОРНАЯ РАБОТА №8

по дисциплине: Организация систем управления и диагностики

на тему: Расчет времени затвердевания непрерывного слитка квадратного сечения (блюмса)
Вариант №10

Исполнитель: Ишемгулов Азамат Ирекович студент 1 курса, гр. ТФм-22

Руководитель: Колдин Александр Викторович, к.т.н., доцент каф. физики

Магнитогорск, 2023

Цель работы: ознакомиться с численным методом решения двухмерных задач нестационарной теплопроводности.

Приборы и принадлежности: компьютер.

Сведения из теории.

Непрерывный слиток квадратного сечения 2δ×2δ (блюмc) вытягивается из неподвижного кристаллизатора с постоянной скоростью u (рис. 8.1).



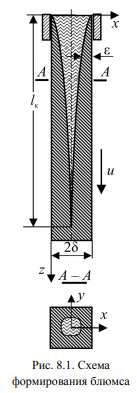
При охлаждении на поверхностях блюмса из жидкой фазы формируется корка затвердевшего металла толщиной ε. На глубине l_к или в момент времени τ_к = l_к/u формирование блюмса завершается. Математическая формулировка задачи по методу сквозного счета включает дифференциальное



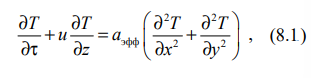
которое в стационарном случае (∂Т/∂τ = 0) принимает вид:



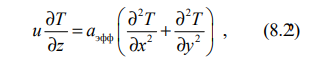
а с учетом кинематического соотношения (u = z/τ) ∂Т/∂(z/u) = ∂Т/∂τ имеем квазистационарное уравнение переноса энергии

---

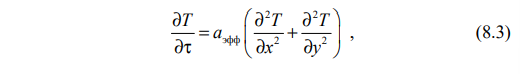
где a_эфф = λ/(ρс_эфф) – эффективная температуропроводность; λ,

ρ – коэффициент теплопроводности и плотность; эффективная теплоемкость скачком возрастает в интервале температур ликвидуса (T_лик) и солидуса (Т_сол) двухфазной зоны и учитывает выделение скрытой теплоты затвердевания (L):



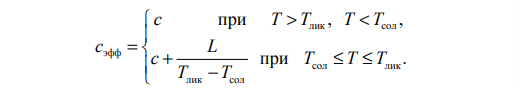
Начальная температура расплава в кристаллизаторе



граничные условия для расчетной области (0 < x < δ,<0


где δТ – перегрев расплава над температурой ликвидуса; Тп – температура поверхности слитка.

В частном случае, когда температура по толщине коркисляба изменяется по линейному закону, решение краевой задачи (8.3–8.5) принимает вид.



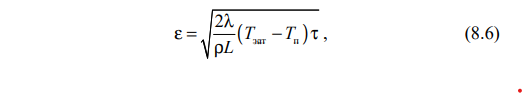
где Т_зат – температура затвердевания, которая находится в интервале температур ликвидуса и солидуса и которая может быть вычислена по формуле Т_зат = (Т_лик + Т_сол) / 2.

Для численного решения задачи на расчетную область наносится регулярная сетка с координатами узлов^





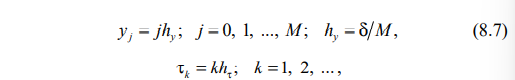
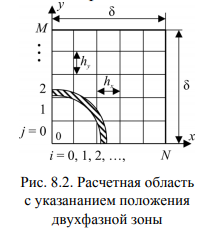
где N, М – числа разбиений расчетной области соответственно в направлении координат x, y, hx, hy, hτ – соответственно шагипространственной (по x, y) и временной (по τ) сеток; i, j, k – номера узловых точек в направлении координат x, y и времени τ. На рис. 8.2 заштриховано возможное положение двухфазной зоны.



Уравнение переноса энергии (8.3) может быть представлено в дискретном виде по явной схеме

---

, в соответствии с которой вторая производная по координатам записывается на «старом» (k–1)-м временном слое с известным распределением температуры. В результате аппроксимации уравнения (8.3)



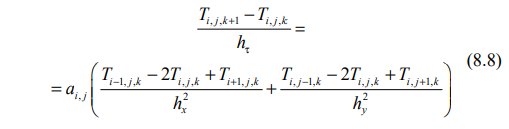
получается явная формула для температуры:



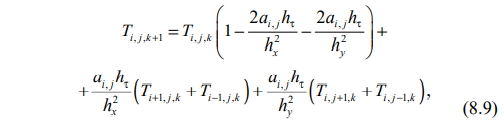
вычисления по которой устойчивы при следующем ограничении на шаг сетки по времени:



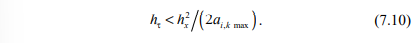
С применением формулы односторонней разности записывается граничное условие на оси симметрии:



С применением формул односторонней разности записываются граничные условия (8.5) на поверхностях блюмса:



а также граничные условия на осях симметрии:



Угловые точки области (0, 0; 0, М; N, 0; N, M) в расчетах не участвуют. Для вычисления температур в угловых точках применяют аппроксимацию стационарного уравнения переноса энергии (8.3). Например, для угловой точки (N, M) (рис. 8.3) это уравнение в конечных разностях принимает вид:





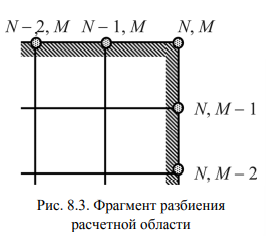
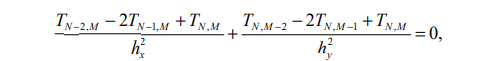
Аналогично для других угловых точек:



Выполнение работа.

В ходе выполнения данной лабораторной работы была составлена Паскаль-программа, реализующая моделирование затвердевания блюмса по явной схеме, представленной в приложении А.

Результат данного моделирования представлен на рисунке 1.



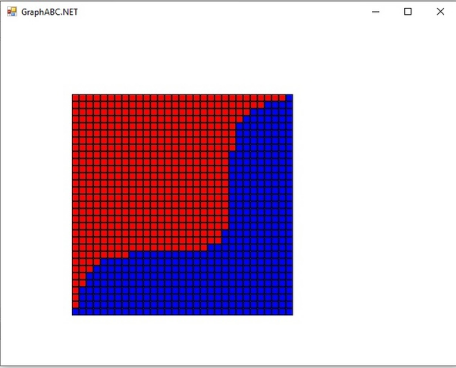
Рисунок 1

Приложение А

program laba8;

uses graphabc;

const

x0 = 100;

y0 = 100;

N = 30;

M = 30;

lx = 0.1;

ly = 0.1;

hx = lx / N;

hy = ly / M;

---

ax = round(lx / N * 3000);

ay = round(ly / M * 3000);

lambda = 50;

rho = 7900;

cp = 457.9;

TS = 1430;

TL = 1500;

L = 270e3;

dT = 10;

a = lambda / cp / rho;

af = lambda / rho / (cp + L / (TL - TS));

Tp = 880;

Tstart = TL + dT;

taumax = 10;
var

i, j: integer;

T: array [0..N, 0..M] of real;

ae: array [0..N, 0..M] of real;

htau, htx, hty, tau, ahtx, ahty: real;
begin

for i := 0 to N do

for j := 0 to M do

T[i, j] := Tstart;

tau := 0;

htau := sqr(hx) * sqr(hy) / a / (sqr(hx) + sqr(hy)) / 6;

htx := htau / sqr(hx);

hty := htau / sqr(hy);

for i:=0 to N do

T[i,M]:=Tp;

for j:=0 to M do

T[N,j]:=Tp;

repeat

{2.1. Определение температуры

на следующем временном слое}

tau := tau + htau;

{2.1.1. Расчёт эффективной температуропроводности}

for i := 0 to N - 1 do

for j := 0 to M - 1 do

begin

if (T[i, j] > Ts) and (T[i, j] < TL)

then ae[i, j] := af

else ae[i, j] := a;

ahtx := ae[i, j] * htx;

ahty := ae[i, j] * hty;

end;

for i := 1 to N-1 do

for j := 1 to M-1 do

T[i, j] := T[i, j] * (1 - 2 * (ahtx + ahty)) + (T[i - 1, j] + T[i + 1, j]) * ahtx + (T[i, j - 1] + T[i, j + 1]) * ahty;

{2.1.3. Расчёт температур в углах

расчётной области}

T[0, 0] := 0.5 * (T[1, 0] + T[0, 1]);

T[0, M] := 0.5 * (T[1, M] + T[0, M - 1]);

T[N, 0] := 0.5 * (T[N - 1, 0] + T[N, 1]);

T[N, M] := 0.5 * (T[N - 1, M] + T[N, M - 1]);

for j := 0 to M do

for i := 0 to N do

begin

Rectangle(x0 + ax * i, y0 + ay * j, x0 + ax * i + ax, y0 + ay * j + ay);

FloodFill(x0 + ax * i + 1, y0 + ay * j + 1, clRed);

end;

for j := 0 to M do

for i := 0 to N do

if T[i, j] < TS then

FloodFill(x0 + ax * i + 1, y0 + ay * j + 1, clBlue);

until tau > taumax;

end.

Контрольные вопросы

1. Конечно-разностное представление первой и второй производных.

2. Явная и неявная схемы аппроксимации уравнения теплопроводности.

3. Соотношение между временным и пространственным шагами сетки, обеспечивающее минимальную ошибку аппроксимации уравнения теплопроводности.

4. Чем объясняется рост корки слитка по закону квадратного корня ?.

5. Запись основных операторов программирования на языке Паскаль

---

Смотрите также файлы

• .docx

• Программа профессиональной переподготовки Основы практической психологии (1150) до.docx

• Бизнесплан (фрагменты) БонМассаж.docx

• 37. 03. 01. Психология.docx

• Повышение урожая сельскохозяйственных культур и его качества.rtf