ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 41
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
М
 ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение
высшего образования
«Тольяттинский государственный университет»
Институт химии и энергетики
(наименование института полностью)
Кафедра /департамент /центр1промышленная электроника
(наименование кафедры/департамента/центра полностью)
13.03.02.
(код и наименование направления подготовки, специальности)
Электроэнергетика электротехника. Электроснабжение
(направленность (профиль) / специализация)
Практическое задание № 1
по учебному курсу «Высшая математика 3
»
(наименование учебного курса)
| Студент | Исаев Данил Сергеевич | |
| | (И.О. Фамилия) | |
| Группа | ЭЭТбп-1901б | |
| | | |
| Преподаватель |
| |
| | (И.О. Фамилия) | |
Контрольная работа 1
Вариант 8 Задача 1
Даны дифференциальные уравнения первого порядка с разделяющимися переменными и их начальные условия. Найти общие решения этих уравнений и определить частные решения.
а) Дано: y′- (y+1)Cosx=0 x=0 y=0
Решение:
Для решения дифференциальные уравнения определим тип уравнения, преобразовав его:
y′- (y+1)Cos x=0
y′= (y+1)Cos x
Разделим обе части на (y+1), д
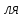 того ,чтобы разделить переменные x и y
того ,чтобы разделить переменные x и y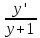 = Cos x при y≠ -1
= Cos x при y≠ -1Следовательно, это дифференциальные уравнения первого порядка с разделяющимися переменными.
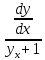 =Cos x
=Cos xПомножим обе части на dx
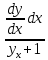 =Cosx dx
=Cosx dx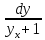 =Cosxdx
=CosxdxВозьмем от обеих частей уравнения интегралы:
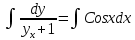
Вычислим по формулам:
∫
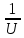 du=ln ∣u∣ +C
du=ln ∣u∣ +C∫Cosxdx= Sinx +C ⇒
Ln(y+1) = Sinx+C ⇒
Y+1=
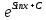
Свойства степеней
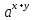 =
=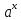 ·
·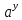
Y=
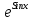 ·
·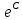 -1 т.к.
-1 т.к.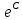 –это константа, то
–это константа, то 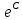 =С ⇒
=С ⇒Y=
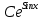 -1 – функция задана неявно.
-1 – функция задана неявно.Выразим функцию через аргумент х явно
Ln(y+1) +
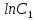 ⇒
⇒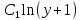 =
=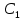
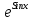
 ⇒ y=
⇒ y=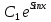 – 1 ⇒
– 1 ⇒Общее решение дифференциального уравнения
y=
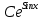 – 1
– 1Найдем частное решение дифференциального уравнения при x=0 y=0:
y=
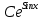
– 1 ⇒ 0=
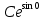 -1
-1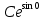 =0 ⇒
=0 ⇒ 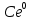 -1=0
-1=0C·1= 1
C = 1
Частное решение дифференциального уравнения:
y=
 – 1
– 1Задача 2.
а) Дано: x
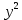 y′- 2 =0
y′- 2 =0 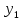 =0
=0 Для решения дифференциальные уравнения определим тип уравнения, преобразовав его: :
x
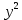 y′- 2 =0
y′- 2 =0 x
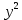 y′= 2
y′= 2 Следовательно, это дифференциальные уравнения первого порядка с разделяющимися переменными.
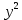 y′ =
y′ =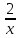 ⇒
⇒ 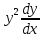 =
= 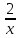 при x ≠ 0
при x ≠ 0Помножим обе части на dx
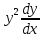 ·dx =
·dx = 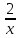 ·dx
·dx 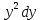 = 2
= 2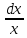
Возьмем от обеих частей уравнения интегралы:
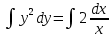
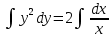
Вычислим по формулам:
∫
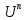 du=
du=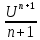 при n= 2
при n= 2∫
 du=ln ∣u∣ ⇒
du=ln ∣u∣ ⇒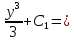 2lnx +
2lnx + 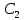
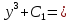 6lnx +
6lnx + 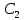 – функция задана неявно.
– функция задана неявно.Выразим функцию через аргумент х явно
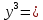 6lnx + C , где
6lnx + C , где 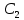
-
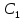 =C
=C Общее решение дифференциального уравнения:
 6lnx + C или
6lnx + C илиY=
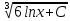
Найдем частное решение дифференциального уравнения при y=0:
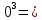 6lnx + C или
6lnx + C илиln
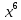 =0
=0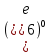 = 1
= 1 1 + C =0
C=-1 ⇒
Частное решение дифференциального уравнения при y=0:
Y=
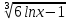
1 Оставить нужное