Добавлен: 07.11.2023
Просмотров: 375
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(3.1)
Гле R- постоянная Ридбера, m и n номера уровней.
В нашем случае n = 1, m = ∞, тогда энергия ионизации
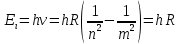(3.2)
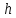- Постоянная планка
Так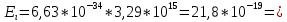
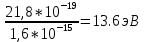
2)Из закона сохранения энергии
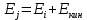(3.3)
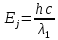-энергия фотона,
с – скорость света
Так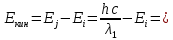
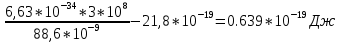
3)Кинетическая энергия электрона
=>
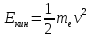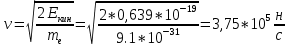
4)В магнитном поле заряженная частица движется под действием силы Лоренца:
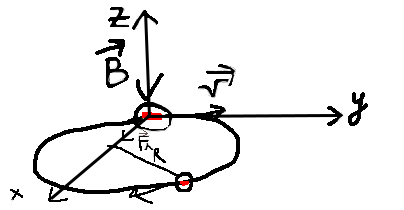
Рис. 4 - движение электронов в магнитном поле
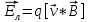(3.4)
q-заряд част.
Так как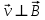
– движение по окружности:
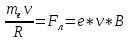(3.5)
q=e
Откуда:
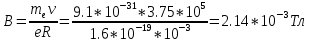
Ответ: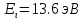
; 
; 
;
.
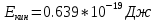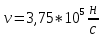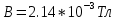Задача 1
Параллельный пучок света с длиной волны λ = 643,8 нм падает по нормали на пластинку из кристалла кварца в половину длины волны перпендикулярно её оптической оси. Показатели преломления для необыкновенного и обыкновенного лучей составляют соответственно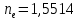
и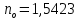 
. Определить: 1) длины волн этих лучей в кристалле; 2) минимальную толщину пластинки; 3) разность фаз между обыкновенным и необыкновенным лучами на выходе из пластинки; 4) уравнение траектории конца результирующего светового вектора для луча на выходе пластинки. Обосновать, какой тип поляризации будет наблюдаться у луча на выходе из пластинки. Изобразите на рисунке ход для необыкновенного и обыкновенного лучей, покажите тип поляризации этих лучей.
Определение показателя преломления:
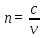
где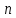
— абсолютный показатель преломления, 
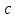— скорость света в вакууме, 
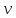— скорость света в среде. Он отражает то, во сколько раз медленнее свет распространяется в среде, чем в вакууме. С другой стороны, зная связь скорости света в среде и ее длины волны:
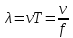
где
— длина волны, 
— скорость света в среде,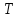 
— период колебаний, f — частота, получаем связь коэффициента преломления и длины волны:
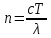
Видно, что в числителе стоит длина волны света в вакууме (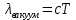
), а в знаменателе длина волны в среде. Выражая искомые длины волн:
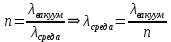
получаем для обыкновенного и необыкновенного лучей:
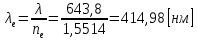
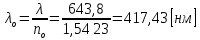
Оптическая длина пути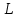
в среде с показателем преломления 
равна произведению геометрической длины пути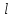 
, пройденного светом, на показатель преломления :
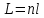
В нашей задаче геометрическая длина пути — это и есть искомая толщина пластинки. Также из условия (пластинка в половину длины волны) ясно, что разность хода (разность оптических длин преломленного (необыкновенного) и непреломленного (обыкновенного)) лучей составляет половину исходной длины волны:
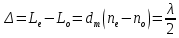
Выражаем искомую величину:
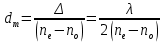
Подставляем значения:
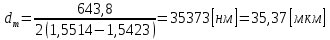
Длина волны — расстояние между точками с одинаковой фазой. Это значит, что разность фаз между точками, расстояние между которыми равно длине волны, составляет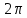
. Это позволяет составить простую пропорцию и выразить искомую величину:
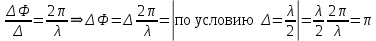
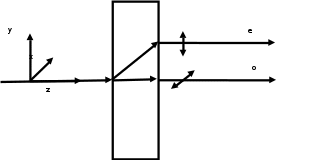
Если свет распространяется перпендикулярно оптической оси, то поляризацию можно разложить на две проекции — параллельную оптической оси и перпендикулярную. Эффективный показатель преломления будет разным для света двух ортогональных поляризаций, и при прохождении через слой (пластинку) материала может наблюдаться сдвиг по фазе между двумя компонентами. Если исходная поляризация линейная и ориентирована либо полностью вдоль, либо полностью перпендикулярно оптической оси, то на выходе из пластинки она не изменится. Однако, если исходно свет поляризован под углом к оптической оси, либо поляризация эллиптическая или циркулярная, то при прохождении через пластинку из одноосного кристалла поляризация может измениться из-за сдвига по фазе между компонентами.
По условию свет изначально имел круговою поляризацию, значит обыкновенный и необыкновенный лучи будут линейно поляризованы и перпендикулярны друг другу.
Введем координатные оси и, учитывая поляризацию света, запишем уравнение траектории конца светового вектора для необыкновенного луча на выходе пластинки:
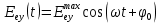
Где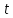
— время, 
— 
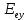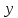-вая компонента вектора напряженности (других компонент нет, так как свет так линейно поляризован), 
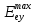— амплитуда, 
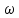— циклическая частота, 
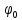— начальная (в момент времени t=0) фаза.
Для обыкновенного луча необходимо учесть, что он поляризован перпендикулярно и имеет сдвиг фазы:
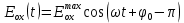
Сдвиг фазы на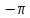
даёт смену знака гармонической функции:
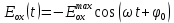
Выразим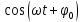
из обоих формул, получим искомое уравнение траектории:
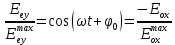
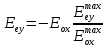
Ответ:????????=414,98нм;????о=417,43нм;????????=35,37мкм;∆Ф=????;????????????=−????????????????????/????????????????????*????????????
Задача 2
Работа выхода электрона из металла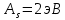
. Поверхность металла облучается фотонами с длиной волны 
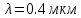. Определить задерживающее напряжение 
для этого опыта. Найти максимальный импульс, передаваемый поверхности металла при вылете каждого электрона (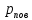
). Во сколько раз отличается импульс выбитого электрона (
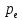) от импульса фотона (
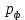), который падает на поверхность? Изобразите на рисунке вольтамперную характеристику фотоэффекта (ВАХ); покажите на ВАХ ток насыщения 
и задерживающий потенциал ( ).
Уравнение фотоэффекта — закон сохранения энергии, который говорит, что энергия кванта излучения (фотона) идет на преодоление электроном работы выхода и приобретение им кинетической энергии.
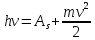
где
— постоянная Планка, 
— частота излучения, их произведение это энергия фотона
Гле R- постоянная Ридбера, m и n номера уровней.
В нашем случае n = 1, m = ∞, тогда энергия ионизации
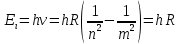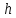(3.2) - Постоянная планкаТак
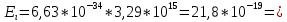
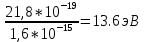
2)Из закона сохранения энергии
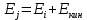(3.3)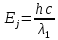 -энергия фотона,с – скорость света
Так
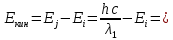
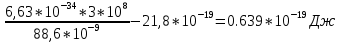
3)Кинетическая энергия электрона
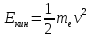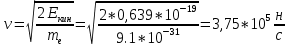
=> 4)В магнитном поле заряженная частица движется под действием силы Лоренца:
Рис. 4 - движение электронов в магнитном поле
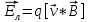(3.4)q-заряд част.
Так как
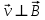– движение по окружности: 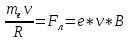(3.5)q=e
Откуда:
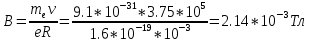
Ответ:
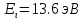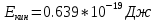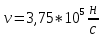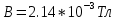; ; ; .5 - ВАРИАНТ
Задача 1
Параллельный пучок света с длиной волны λ = 643,8 нм падает по нормали на пластинку из кристалла кварца в половину длины волны перпендикулярно её оптической оси. Показатели преломления для необыкновенного и обыкновенного лучей составляют соответственно
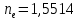и 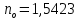. Определить: 1) длины волн этих лучей в кристалле; 2) минимальную толщину пластинки; 3) разность фаз между обыкновенным и необыкновенным лучами на выходе из пластинки; 4) уравнение траектории конца результирующего светового вектора для луча на выходе пластинки. Обосновать, какой тип поляризации будет наблюдаться у луча на выходе из пластинки. Изобразите на рисунке ход для необыкновенного и обыкновенного лучей, покажите тип поляризации этих лучей.| Дано: 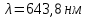 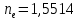 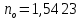| Решение: |
| Найти:      | |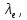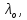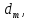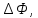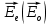
Определение показателя преломления:
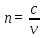
где
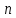— абсолютный показатель преломления, 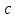— скорость света в вакууме, 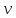— скорость света в среде. Он отражает то, во сколько раз медленнее свет распространяется в среде, чем в вакууме. С другой стороны, зная связь скорости света в среде и ее длины волны:
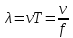
где
— длина волны, — скорость света в среде, 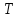— период колебаний, f — частота, получаем связь коэффициента преломления и длины волны: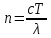 Видно, что в числителе стоит длина волны света в вакууме (
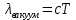), а в знаменателе длина волны в среде. Выражая искомые длины волн: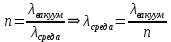 получаем для обыкновенного и необыкновенного лучей:
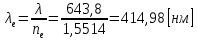
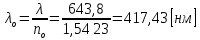
Оптическая длина пути
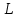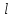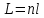
в среде с показателем преломления равна произведению геометрической длины пути , пройденного светом, на показатель преломления : В нашей задаче геометрическая длина пути — это и есть искомая толщина пластинки. Также из условия (пластинка в половину длины волны) ясно, что разность хода (разность оптических длин преломленного (необыкновенного) и непреломленного (обыкновенного)) лучей составляет половину исходной длины волны:
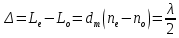
Выражаем искомую величину:
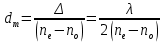
Подставляем значения:
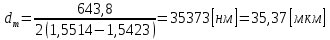
Длина волны — расстояние между точками с одинаковой фазой. Это значит, что разность фаз между точками, расстояние между которыми равно длине волны, составляет
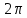. Это позволяет составить простую пропорцию и выразить искомую величину: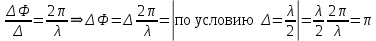 Если свет распространяется перпендикулярно оптической оси, то поляризацию можно разложить на две проекции — параллельную оптической оси и перпендикулярную. Эффективный показатель преломления будет разным для света двух ортогональных поляризаций, и при прохождении через слой (пластинку) материала может наблюдаться сдвиг по фазе между двумя компонентами. Если исходная поляризация линейная и ориентирована либо полностью вдоль, либо полностью перпендикулярно оптической оси, то на выходе из пластинки она не изменится. Однако, если исходно свет поляризован под углом к оптической оси, либо поляризация эллиптическая или циркулярная, то при прохождении через пластинку из одноосного кристалла поляризация может измениться из-за сдвига по фазе между компонентами.
По условию свет изначально имел круговою поляризацию, значит обыкновенный и необыкновенный лучи будут линейно поляризованы и перпендикулярны друг другу.
Введем координатные оси и, учитывая поляризацию света, запишем уравнение траектории конца светового вектора для необыкновенного луча на выходе пластинки:
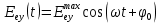
Где
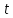— время, 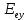— 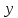-вая компонента вектора напряженности (других компонент нет, так как свет так линейно поляризован), 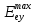— амплитуда, 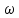— циклическая частота, 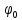— начальная (в момент времени t=0) фаза.Для обыкновенного луча необходимо учесть, что он поляризован перпендикулярно и имеет сдвиг фазы:
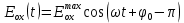
Сдвиг фазы на
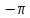даёт смену знака гармонической функции: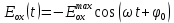 Выразим
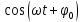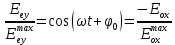
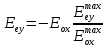
из обоих формул, получим искомое уравнение траектории: Ответ:????????=414,98нм;????о=417,43нм;????????=35,37мкм;∆Ф=????;????????????=−????????????????????/????????????????????*????????????
Задача 2
Работа выхода электрона из металла
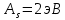. Поверхность металла облучается фотонами с длиной волны 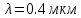. Определить задерживающее напряжение для этого опыта. Найти максимальный импульс, передаваемый поверхности металла при вылете каждого электрона (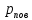 ). Во сколько раз отличается импульс выбитого электрона ( 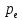) от импульса фотона ( 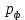), который падает на поверхность? Изобразите на рисунке вольтамперную характеристику фотоэффекта (ВАХ); покажите на ВАХ ток насыщения и задерживающий потенциал ( ).| Дано: 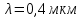 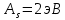| Решение: |
| Найти:    | |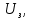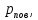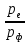
Уравнение фотоэффекта — закон сохранения энергии, который говорит, что энергия кванта излучения (фотона) идет на преодоление электроном работы выхода и приобретение им кинетической энергии.
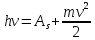
где
— постоянная Планка, — частота излучения, их произведение это энергия фотона