Добавлен: 07.11.2023
Просмотров: 359
Скачиваний: 8
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
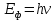 ,
, 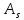 — работа выхода, энергия, которую надо потратить, чтобы электрон покинул материал,
— работа выхода, энергия, которую надо потратить, чтобы электрон покинул материал, 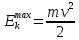 — максимальная кинетическая энергия электрона.
— максимальная кинетическая энергия электрона.Запирающее напряжение — это обратное напряжение, которое нужно подать на анод и катод, чтобы ток, который появляется в ходе фотоэффекта прекратился. Работа этого поля должна компенсировать кинетическую энергию электронов.
Связь работы и напряжения:
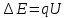 где
где 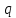 – заряд,
– заряд, 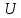 – напряжение,
– напряжение, 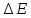 – приращение энергии, работа. В нашем случае речь идет об электроне поэтому
– приращение энергии, работа. В нашем случае речь идет об электроне поэтому 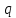 заменим на
заменим на 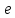 – заряд электрона. Тогда получим:
– заряд электрона. Тогда получим: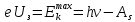
Связь длины волны, частоты и скорости:
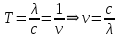
Выражаем искомую величину, подставляем значения (важно заметить, что работа выхода нам дана в электрон-вольтах, соответственно, ее пересчитываем):
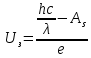
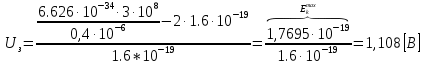
По закону сохранения импульса, поверхность испытывает “отдачу” равную импульсу выбитого электрона.
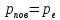
Кинетическую энергию электрона мы нашли при ответе на прошлый вопрос. Через неё найдем импульс электрона и соответственно искомую величину:
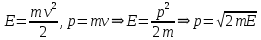
В нашем случае
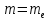 — масса электрона. Таким образом:
— масса электрона. Таким образом: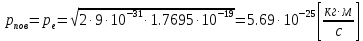
Импульс фотона:
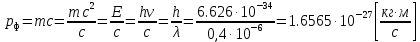
крипч
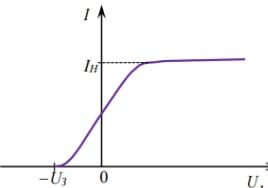
Напряжении, при котором сила тока в фотоэлементе обращается в ноль,
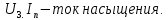
держивающим напряжением ????з.
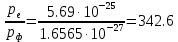
Ответ:
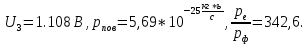
Задача 3
Атомарный водород, находящийся в основном состоянии, облучается монохроматическим светом с длиной волны 121,58 нм и переходит в возбужденное состояние. Определить радиус
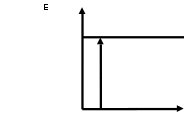
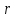 боровской орбиты этого возбужденного состояния. Изобразите на рисунке энергетическую диаграмму атома водорода, покажите на ней переход из основного в возбужденное состояние.
боровской орбиты этого возбужденного состояния. Изобразите на рисунке энергетическую диаграмму атома водорода, покажите на ней переход из основного в возбужденное состояние.| Дано: 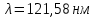 | Решение: |
| Найти: 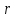 бок.ор. бок.ор. | |
Энергия фотона расходуются на возбуждение атома. Разность между энергией возбужденного состояния и основного равно энергии фотона. Энергия основного состояния, это энергия, которую требуется потратить для полной ионизации газа.
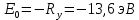 , где
, где 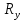 — постоянная Ридберга:
— постоянная Ридберга: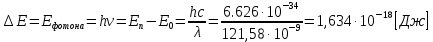
Для удобства пересчитаем в электрон-вольтах:
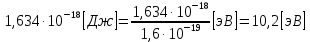
Энергия
 –того состояния:
–того состояния: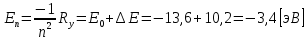
Отсюда:
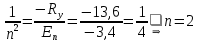
Радиус атома в -том состоянии:
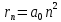
где
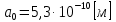 — боровский радиус (радиус ближайшей к ядру орбиты электрона).
— боровский радиус (радиус ближайшей к ядру орбиты электрона).
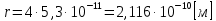
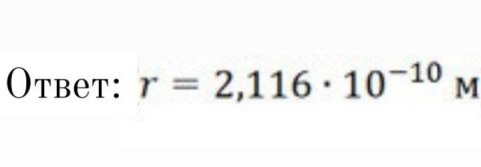
6 - ВАРИАНТ
-
Монохроматический свет падает нормально на щель шириной 10 мкм. За щелью находится тонкая линза с оптической силой 4Дптр. В фокальной плоскости линзы расположен экран. Найти длину волны света ????, если расстояние между симметрично расположенными минимумами второго порядка равно 6 см. Приведите рисунок для схемы установки. Изобразите дифракционную картину интенсивности света на экране. Пронумеруйте все дифракционные максимумы, которые могут быть видны на экране. (???? = 595,7нм)
| Дано: 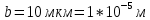 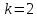 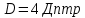 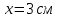 | Решение: 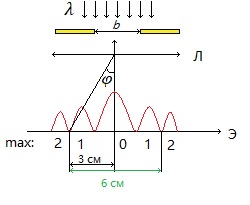 |
| Найти: 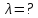 |
Нам нужно найти длину волны
 . Ее мы можем выразить из условия наблюдения дифракционного минимума:
. Ее мы можем выразить из условия наблюдения дифракционного минимума: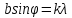 1.1
1.1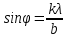
Где
 , порядок дифракционного минимума, у нас по условию
, порядок дифракционного минимума, у нас по условию 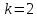 .
.Фокусное расстояние линзы определим из ее оптической силы:
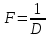 1.2
1.2 Из формул 1.1 и 1.2 мы можем вывести формулу для расстояния от центра дифракционной картины до минимума второго порядка:
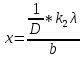 1.3
1.3Нам дано расстояние между симметрично расположенными минимумами второго порядка = 6 см, но для
 нам нужно расстояние от центра дифракционной картины до минимума второго порядка, которое исходя из рисунка является нашим катетом.
нам нужно расстояние от центра дифракционной картины до минимума второго порядка, которое исходя из рисунка является нашим катетом. Отсюда:
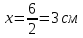
.
Выразим из 1.3 длину волны λ:
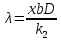 1.4
1.4Подставим числовые значения:
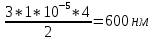
Ответ: длина волны λ = 600 нм.
-
Температура абсолютно черного тела увеличилась в 1,5 раза, в результате чего длина волны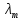 , на которую приходится максимум энергии излучения, изменилась на
, на которую приходится максимум энергии излучения, изменилась на 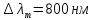 . Определить начальную
. Определить начальную 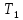 и конечную
и конечную 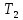 температуру тела. Во сколько раз в результате нагревания изменилась тепловая мощность, излучаемая телом? Рисунком поясните график распределения энергии в спектре излучения абсолютно чёрного тела, укажите для данных температур положение
температуру тела. Во сколько раз в результате нагревания изменилась тепловая мощность, излучаемая телом? Рисунком поясните график распределения энергии в спектре излучения абсолютно чёрного тела, укажите для данных температур положение 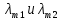 . (
. (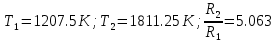 )
)
| Дано: 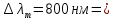 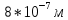 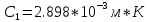 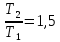 | Решение: 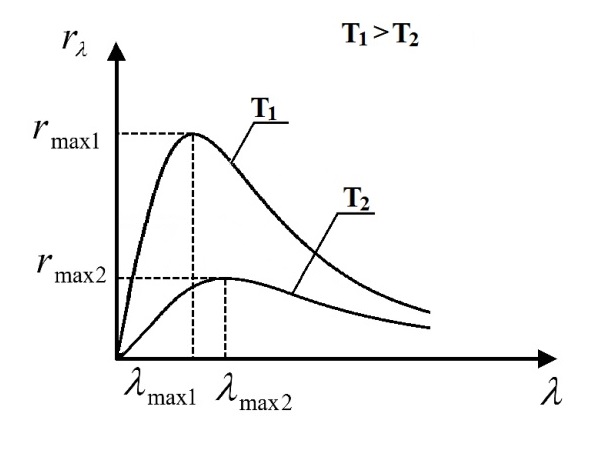 |
| Найти: 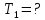 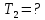 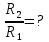 |
Воспользуемся законом смещения Вина: длина волны, на которую приходится максимум излучательной способности а.ч.т.
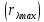 обратно пропорционален абсолютной температуре этого тела. Для любого а.ч.т. постоянная
обратно пропорционален абсолютной температуре этого тела. Для любого а.ч.т. постоянная 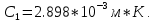
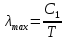 2.1
2.1 По условию задачи температура абсолютно черного тела увеличилась в 1.5 раза: