Файл: Вариант 12 x 1 v1 X2 X3 X4 v3 v7 v10 v6 v8 v11 v4 v9 v5 v2 X5 X6 X7 v12 X8 Дать словесное описание графа.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 14
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вариант 12
X
1 v1 X2 X3 X4v3 v7 v10
v6 v8
v11
v4 v9
v5
v2
X5 X6 X7 v12 X8
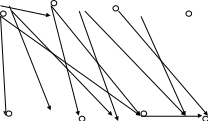
1. Дать словесное описание графа
-
Исходный граф является ориентированным т.к. все связи являются дугами
Чтобы получить из орграфа неорграф, заменим все дуги на ребра:
X1 v1 X2 X3
X4V3 v7 v10
v6 V8
V11
V9
V2 V4
V5
V12
X5 X6 X7 X8
Чтобы получить из орграфа смешенный граф заменим дуги V2 и V12 на ребра
X
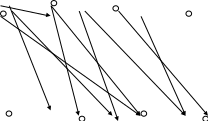1 v1 X2 X3 X4
v3 v7 v10
v6 v8
v11
v4 v9
v5
v2
X5 X6 X7 v12 X8
1.2. Граф является неполным т.к. не любые две его вершины соединены друг с другом. Чтобы сделать полный граф, соединим все его вершины.
1.3. Исходный граф является простым т.к. отсутствуют петли и кратные связи.
Для того чтобы получить мультиграф добавим дугу V13
X
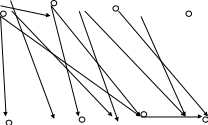1 v1 X2 X3 X4v3 v7 v10
v6 v8
v13 v11
v4 v9
v5v2
X5 X6 X7 v12 X8
Для того чтобы получить псевдограф к любой вершине добавим петлю.
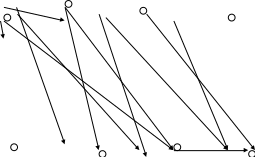
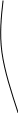
1.4. Исходный граф является планарным т.к. его дуги пересекаются.
Чтобы сделать его плоским удалим v7 v9 v6
X
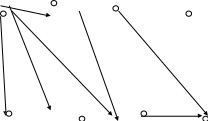1 v1 X2 X3 X4
v10
v8
v11
v4
v5
v2
X5 X6 X7 v12 X8
v3
1.5.
Чтобы получить из данного графа лес удалим: V2, V5, V6, V7, V8, V11, V12
Чтобы получить из данного графа дерево удалим: V3, V4, V5, V7, V8, V9, V12 и добавим:V13, V14
V13 V14 1.6.
Данный граф не связен, так как из вершины невозможно попасть ни в одну другие.
Чтобы данный граф был связен сменим направление дуги V12.
X
1 v1 X2 X3 X4v3 v7 v10
v6 v8
v11
v4 v9
v5
v2
X5 X6 X7 v12 X8
1.7 Данный граф не бихроматический или двудольный.
Чтобы сделать граф двудольным добавим 2 вершины: Х(1-2) и Х(3-8)
X1 x2 X3 X4 x8 X5 x6 х7 х1-2 х3-8
2. Множество вершин: Х={x1,x2,x3,x4,x5,x6,x7,x8}
Множество дуг: {{x1,x2},{x1,x7},{x2,x5},{x2,x6},{x3,x8},{x4,x6},
{x5,x1},{x5,x3},{x5,x3},{x7,x2},{x7,x4},{x7,x8}}
Матрица смежности
| | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 |
| X1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| X2 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| X3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| X4 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| X5 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| X6 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| X7 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 |
| X8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Матрица инцидентности
| | V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | V10 | V11 | V12 |
| X1 | 1 | -1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| X2 | -1 | 0 | 0 | 1 | 0 | 1 | -1 | 0 | 0 | 0 | 0 | 0 |
| X3 | 0 | 0 | 0 | 0 | -1 | 0 | 0 | -1 | 0 | 1 | 0 | 0 |
| X4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | -1 | 0 |
| X5 | 0 | 1 | 0 | -1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| X6 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 1 | -1 | 0 | 0 | 0 |
| X7 | 0 | 0 | -1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| X8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | -1 |
3. Число дуг - 12;
число вершин – 8;