коэффициент связности графа – 1;

	X1	X2	X3	X4	X5	X6	X7	X8
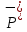(xi)	2	2	1	1	2	1	3	0
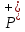(xi)	1	2	2	1	1	2	1	2
P (xi)	3	4	3	2	3	3	4	2

1. 
   ∑P(xi)=3+4+3+2+3+3+4+2=24
   
2. 
   ∑P(xi)=2*12=24, (где 12 - кол-во дуг и ребер)
   

степени всех вершин графа – 24;

цикломатическое число графа υ(G) = m – n + q = 12 – 8 + 1 = 7, где m – число дуг, n – число вершин, q - число компонент связности;

число компонент связности – 1;

эксцентриситет :

r(x1) = 2 ,

r(x2) = 2 ,

r(x3) = 2 ,

r(x4) = 3 ,

r(x5) = 3,

r(x6) = 2 ,

r(x7) = 2 ,

r(x8) = 2 ,

диаметр D = 3 ;

радиус R = min r(xi) =2 .

Кратчайшее расстояние между вершинами:



4. Вершинная раскраска

---

1 1

3 1

2 2 2 3
С1 = {x2, x3, x4}

С2 = {x5, x6, x7 }

С3 = {x1, x8}

Хроматическое число = 3.
5. Реберная раскраска
1

4

3

3 2

2

3

1 2

2

1

1

С1 = {{x1,x2},{x3,x5},{x4,x6},{x7,x8}}

С2 = {{x1,x5},{x2,x6},{x4,x7},{x3,x8}}

С3 = {{x1,x7},{x2,x5},{x3,x6}}
С4 = {x2,x7}

Хроматическое число = 4.

6.
Данный ориентированный граф не содержит Эйлеров цикл, он не сильно связан и для шести вершин (Х1, Х3, Х5, Х6, Х7, Х8) графа полустепень захода не равна полустепени исхода.
Чтобы получить Эйлеровый граф добавим дуги V13 и V 14, и сменим направление дуги V12.

V13




X 1 v1 X2 X3 X4

v3 v7 v10

v6 v8

v11

v4 v9
v5

v2




X5 V14 X6 X7 v12 X8


7.

Гамильтонов путь существует:

---

Х2 - Х5 - Х1 - Х7 - Х4 - Х6 - Х3 - Х8

Гамильтонов цикл отсутствует, т.к. из конечной вершины мы не можем попасть в начальную. Раз нет цикла, то граф не Гамильтонов.
Чтобы преобразовать данный граф до Гамильтонова надо добавить дугу V13=(X8X2)
v13




X 1 v1 X2 X3 X4

v3 v7 v10

v6 v8

v11

v4 v9
v5

v2
X5 X6 X7 v12 X8
9.С помощью алгоритма выделения минимального остовного дерева получить остов.
X 1 X2 X 1 X2




X5

---

10. Вершинная независимость.
Матрица смежности

	X1	X2	X3	X4	X5	X6	X7	X8
X1	0	1	0	0	0	0	1	0
X2	0	0	0	0	1	1	0	0
X3	0	0	0	0	0	0	0	1
X4	0	0	0	0	0	1	0	0
X5	1	0	1	0	0	0	0	0
X6	0	0	1	0	0	0	0	0
X7	0	1	0	1	0	0	0	1
X8	0	0	0	0	0	0	0	0

(x1 v x2) (x1 v x7) (x2 v x5) (x2 v x6)(x3 v x8) (x4 v x6) (x5 v x1) (x5 v x3) & & (x6 v x3)(x7 v x2) (x7 v x4) (x7 v x8)= (x2 v x1x5x6x7)(x3 v x5x6 x8) & & (x7 v x1x4x8)(x4 v x6) (x5 v x1)=(x2x3 v x1x3x5x6x7 v x2x5x6x8 v
v x1x5x6x7x8) (x7 v x1x4x8) (x4x5 v x4x1 v x6x5 v x6x1)=
=(x2x3 v x1x3x5x6x7 v x2x5x6x8 v x1x5x6x7x8) (x4x5x7 v x1x4x7 v x5x6x7 v x1x6x7 v x1x4x5x8 v x1x4x8 v x1x4x5x6x8 v x1x4x6x8)=

---

=(x2x3x4x5x7 v x1x3x4x5x6x7 v x2x4x5x6 x7x8 v x1x4x5x6x7x8 v
v x1x2x3x4x7 v x1x3x4x5x6x7 v x1x2x4x5x6x7x8 v x1x4x5x6x7x8 v

v x2x3x5x6x7 v x1x3x5x6x7 v x2x5x6x7x8 v x1x5x6x7x8 v x1x2x3x6x7 v x1x3x5x6x7 v x1x2x5x6x7x8 v x1x5x6x7x8 v

v x1x2x3x4x5x8 v x1x3x4x5x6x7x8 v x1x4 x2x5x6x8 v x1x4x5x6x7x8 v

v x1x2x3x4x8 v x1x3x4x5x6x7x8 v x1x2x4x5x6x8 v x1x4x5x6x7x8 v

v x1x2x3x4x5x6x8 v x1x3x4x5x6x7x8 v x1 x2x4x5x6x8 v x1x4x5x6x7x8 v

v x1x2x3x4x6x8 v x1x3x4x5x6x7x8 v x1x2x4x5x6x8 v x1x4x5x6x7x8) =
= (x2x3x4x5x7 v x2x4x5x6 x7x8 v x1x2x3x4x7 v x1x3x4x5x6x7 v x1x2x4x5x6x7x8 v x2x3x5x6x7 v x2x5x6x7x8 v x1x5x6x7x8 v x1x2x3x6x7 v x1x3x5x6x7 v x1x2x5x6x7x8 v x1x2x3x4x5x8 v x1x4x2x5x6x8 v x1x2x3x4x8 v x1x2x4x5x6x8 v x1x2x3x4x5x6x8 v x1x2x3x4x6x8 v x1x4x5x6x7x8)=
=(x2x3x4x5x7 v x1x2x3x4x7 v x2x3x5x6x7 v x2x5x6x7x8 v x1x5x6x7x8 v x1x2x3x6x7 v x1x3x5x6x7 v x1x2x3x4x8 v x1x2x4x5x6x8)

Подмножества независимых вершин: {x5,x6,x8},{x5,x6,x8},{x1,x4,x8},{x1,x3,x4}, {x2x3x4}{ x4x5x7}{ x2x4x8}, {x5x6x7},{x3x7}

Доминирование.

	X1	X2	X3	X4	X5	X6	X7	X8
X1	1	1	0	0	0	0	1	0
X2	0	1	0	0	1	1	0	0
X3	0	0	1	0	0	0	0	1
X4	0	0	0	1	0	1	0	0
X5	1	0	1	0	1	0	0	0
X6	0	0	1	0	0	1	0	0
X7	0	1	0	1	0	0	1	1
X8	0	0	0	0	0	0	0	1

(x1 v x2 v x7) (x2 v x5 v x6) (x3 v x8) (x4 v x6) (x1 v x3 v x5) (x3 v x6)

(x2 v x4 v x7 v x8) (x8)=

= (x1x2 v x1x5 v x1x6 v x2 v x2x5 v x2x6 v x2x7 v x5x7 v x6x7) (x3x4 v x3x6 v x4x8 v x6x8) (x1x3 v x3 v x3x5 v x1x6 v x3x6 v x5x6)

---

Смотрите также файлы

• Понятие Определение или характеристика, либо окончание предложения.docx

• Контрольные вопросы по курсу " Дискретная математика".docx

• 1. Построить граф биологической классификации видов. Используя граф, определить, какими признаками будут обладать следующие существа.docx

• Реферат по культурологии Жена путешественника во времени.doc

• Расчет усилительного каскада с общим эмиттером.docx